Solving Large Geometric and Visualization Problems with GPU Computing in MATLAB
By Paul Peeling, MathWorks
It is often necessary to scale a technical computing problem involving a small amount of data to a much larger data set. Simply looping over each section of the data can become a computational bottleneck, especially if the application has to run in real time. MATLAB® offers several approaches for accelerating algorithms, including performing computations in parallel on multicore processors and GPUs. If you have an NVDIA GPU available, one approach is to leverage the parallel architecture and throughput of the GPU with Parallel Computing Toolbox™. Certain classes of problems, especially in computational geometry and visualization, can be solved very efficiently on a GPU.
In this article we will modify an algorithm to run on a GPU, and then solve a geometric problem involving millions of lines and shapes in under a second. We illustrate this approach using the problem of tracing light rays as they intersect with objects. This type of problem is present in a variety of applications, including scene rendering and medical imaging.
The code in this example is available for download.
Scene Rendering Example
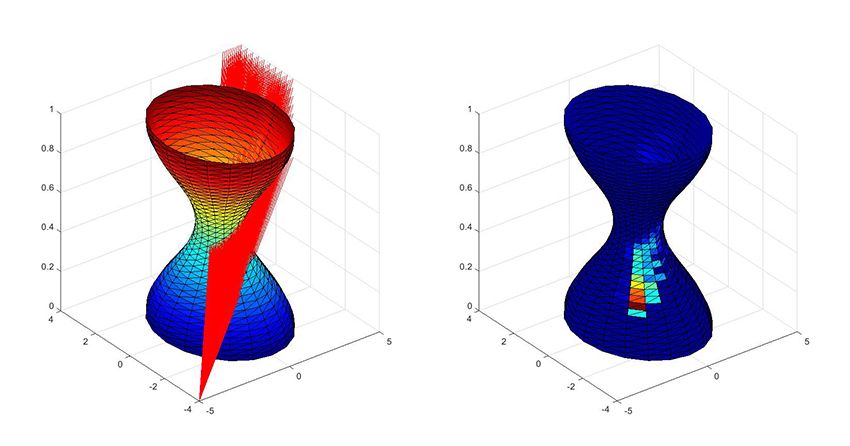
Our goal is to render a scene that is lit by a directed light source. We have created a triangulated surface and drawn a set of rays emanating from the corner that intersect with the object (Figure 1). Using MATLAB, we can determine how many rays intersect with each triangle in the object. This information can be used to calculate the intensity of light hitting the surface, and thus, how the light should be rendered.
The core algorithm we will implement determines whether a line intersects with a triangle. This algorithm accepts five sets of input coordinates as vectors, and it returns a flag if the line intersects with the triangle.
Reading through the function, we discover that it only operates on a single line and on a single triangle per call.
function flag = rayTriangleIntersection(origin, direction, p0, p1, p2)
For our application, we will need to loop over all the rays in the scene and all the triangles on the surface. Since there are 780 triangles and 1000 rays in the example, we will need to call this function 780,000 times. As we scale up to larger and more complex scenes, this algorithm will become a computational bottleneck.
Strategies for Acceleration
There are several techniques we could use to accelerate this algorithm. For example:
- Vectorizing—modifying the function to accept multiple lines or triangles in a single call
- Writing a MEX function to loop over the data in C code
- Dividing the problem into smaller problems and distributing it to workers using Parallel Computing Toolbox
- Modifying the algorithm to run in parallel on a GPU
Each of these techniques involves modifying, testing, and benchmarking code. To select the method that will perform best, we need to understand more about the algorithm.
First, we note that the amount of computation is much larger than the amount of data. If there are R rays and T triangles, we will need 3x(R+T) points to describe the scene, yet the number of intersections to be calculated is RxT.
Second, the calculation at each possible intersection point is independent and contains only a small amount of switching logic. Problems that require much more computation than data, and for which the computations can be executed independently, are well suited to the architecture of a GPU.
As the algorithm takes a fixed number of inputs with constant dimensions and returns only scalar outputs, we can recode the algorithm using arrayfun and then execute the algorithm directly on the GPU. arrayfun is a MATLAB function that applies a specified function to each element of a set of arrays. If one of the arrays is a gpuArray, the function is executed on the GPU.
Making the Function Compatible with arrayfun
A function that can be called using arrayfun must have only scalar input and output arguments. We expand each three-element vector in the original list of input arguments into each X,Y,Z coordinate.
function flag = rayTriangleIntersection_gpu (ox,oy,oz,... dx,dy,dz,... p0x,p0y,p0z,... p1x,p1y,p1z,... p2x,p2y,p2z)
We then convert the remainder of the algorithm to use the scalar valued arguments. For instance, this line of code subtracts two of the triangle vertices:
e2 = p2-p0;
We perform the subtraction explicitly for each dimension:
e2x = p2x-p0x; e2y = p2y-p0y; e2z = p2z-p0z;
To avoid coding errors, we can use helper functions to encapsulate operations like a vector cross product.
q = cross(d,e2);
is now be written as
[qx,qy,qz] = cross_product(dx,dy,dz,e2x,e2y,e2z);
where the helper function is defined as
function [w1,w2,w3] = cross_product(u1,u2,u3,v1,v2,v3)
w1 = u2*v3 - u3*v2; w2 = u3*v1 - u1*v3; w3 = u1*v2 - u2*v1; end
Calling the Function with gpuArray Input Arguments
In the MATLAB workspace, we have created matrices A, B, and C for the vertices of the triangles in the object with dimensions 3xT, where T is the number of triangles, and a matrix D containing the direction vectors of each ray, with dimensions Rx3, where R is the number of lines.
To execute arrayfun on the GPU, at least one of these matrices must be explicitly moved to the GPU.
gD = gpuArray(D);
We then call arrayfun directly, passing in each column of the triangle vertex matrices and each row of the direction vectors separately. arrayfun converts the other input arguments to GPU arrays and expands the arguments along singleton dimensions to match the dimensions of the other inputs. In this case, the origin is expanded along the number of lines and triangles. The triangles are replicated for every line, and vice-versa.
H = arrayfun( @rayTriangleIntersection_gpu, ...
origin(1), origin(2), origin(3), ...
gD(:,1),gD(:,2),gD(:,3), ...
A(:,1),B(:,1),C(:,1), ...
A(:,2),B(:,2),C(:,2), ...
A(:,3),B(:,3),C(:,3) );
Once we have calculated all the intersections, we need to calculate the number of intersections per triangle. We can perform this calculation on the GPU and then pass the result back to MATLAB for visualizing on the surface.
numhits = gather(sum(H,1));
Notice that we try to limit the amount of data being passed to and from the GPU. The coordinates of the scene need to be replicated for every intersection. We could do this by using repmat on the matrices in the MATLAB workspace and then transferring the matrices to the GPU. However, this approach involves transferring much more data than if we passed the original data to the GPU and let arrayfun handle how the coordinates are combined with each intersection.
Similarly, we only retrieve the number of hits per triangle from the GPU, not the full set of intersections. Minimizing the amount of data transferred can significantly reduce the time taken for GPU computations.
Comparing Approaches
With some practice and reuse of helper functions, it is possible to modify the algorithm to run on the GPU using arrayfun in the same amount of time it would take an experienced MATLAB programmer to vectorize the code. Using the existing MATLAB code to generate the scene and calculate intersections by looping over each line and triangle, we find the time taken to process the 780,000 intersections shown in Figure 1 shrinks from 46 seconds to 3 milliseconds!
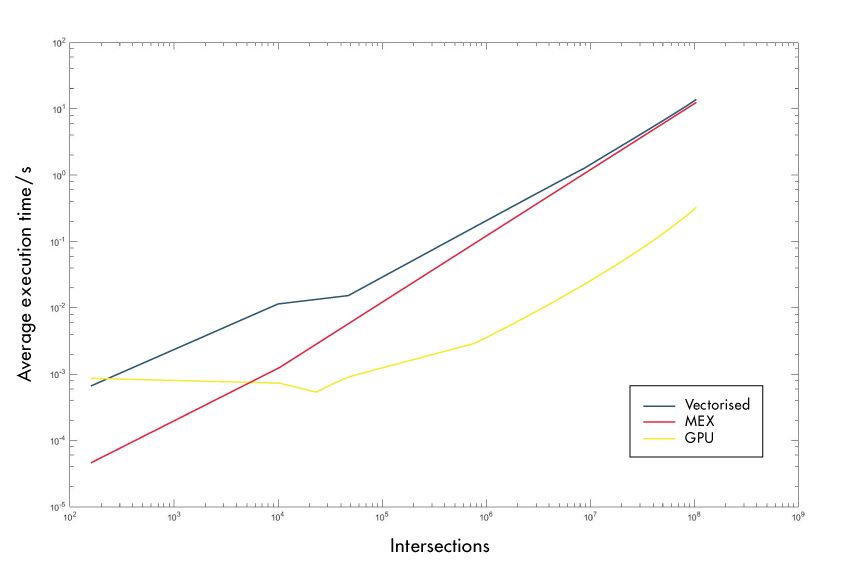
Clearly, this is a substantial improvement. We also should demonstrate that the approach scales to much larger problems and that using a GPU was a better choice for this type of problem than other acceleration strategies. The plot in Figure 2 compares the execution time for larger scenes when using our GPU algorithm, a vectorized version, and a MEX file created using MATLAB Coder™. The functions timeit and gputimeit were used to estimate the average execution time for different numbers of possible intersections.
As Figure 2 shows, the parallelization offered by the GPU gives superior performance both for relatively simple scenes (100,000 intersections) and for scenes that are orders of magnitude more complex.
Extending this Approach
We presented several characteristics of a large geometric problem that make it suitable for solving with a GPU using arrayfun. We then showed how to modify the code to compute the algorithm with minimal data transfer to and from the GPU. The algorithm runs substantially faster on the GPU than it did using other acceleration approaches referred to in this article.
This approach can be used to accelerate many other algorithms. Any problem that involves computing an interaction between every combination of elements in a data set is worth considering, as the amount of data involved is less than the amount of computation required.
Common operations such as matrix multiplication and computing fast Fourier transforms have this property. Many of these operations have been implemented for the GPU in Parallel Computing Toolbox.
Here are two more ideas to try:
- Computing intersections of rays and boxes. This approach is often used to reduce the number of possible intersections for complex objects before applying the algorithm to find the actual intersections.
- Searching two time series for the time at which they most strongly correlate in order to compute the alignment of the two sequences. The function
xcorrin Signal Processing Toolbox™ is a good starting point. An implementation ofxcorroptimized for running on the GPU is now available when used with Parallel Computing Toolbox.
We have seen how MATLAB algorithms can easily be modified to run on a GPU using the arrayfun approach and Parallel Computing Toolbox. For problems involving large amounts of data, the arrayfun approach can significantly outperform vectorization and MEX approaches.
Published 2014 - 92206v00