Using MATLAB to Teach Problem-Solving Techniques to First-Year Liberal Arts Students
By Dr. Robert Talbert, Franklin College
The students taking CMP 150: Computer Tools for Problem Solving at Franklin College this spring were not the ones who usually take a MATLAB class. Few were engineering or science majors, and fewer still had any programming experience. Most were pursuing a degree in education, and were taking the course because it is a prerequisite for Calculus 3.
While learning MATLAB might not seem essential to a liberal arts education, the ability to use technology and critical thinking to solve problems undoubtedly is. I know that most of the students in CMP 150 will eventually forget function names, commands, and other details, but that's not vital. What is important is that they learn how to use MATLAB to solve problems by themselves.
Course Motivation
CMP 150 was created to provide students with programming experience in their first year and to enable them to fulfill a requirement of our dual-degree engineering program.
For many years, mathematics majors at Franklin College were required to take an introductory C++ programming course. Several former students told us that they would have benefited from more applicable programming experience. Many of these recent graduates noted that, while they don't write software in C++, they often need to write quick, functional blocks of code to solve a problem or perform an analysis that would be difficult to do using a spreadsheet.
Adding CMP 150 to our mathematics curriculum enabled us to respond to the feedback we received from Franklin College graduates. It also helped us achieve a major goal of our curriculum revision: to integrate programming into many more courses, including Linear Algebra, Calculus 3, and Numerical Methods.
CMP 150 also helped the Franklin College undergraduates enrolled in our dual-degree engineering program with the Purdue University School of Engineering and Technology at Indianapolis, which requires three years at Franklin College and a further two years at Indiana University – Purdue University – Indianapolis (IUPUI). In the past, these students took a required MATLAB course at IUPUI. During our curriculum revision, we decided to create our own version, covering the same topics as the Purdue course but aligning them more closely with the rest of our coursework.

The Inverted Classroom
CMP 150 meets just one day a week for 75 minutes. To make the most of this limited classroom time I employ an inverted classroom model. In this model, the students watch video lectures, complete online tutorials, and do the required reading at home. Class time is devoted to hands-on lab exercises, with virtually no lecture. This arrangement enables me to spend time with the students as they work in groups of two or three on their weekly assignments (Figure 1). Although it took the students some time to adjust to this way of learning, by the end of the semester they had refined an invaluable skill: the ability to learn and apply new concepts on their own.
The video lectures and tutorials are easily scalable. In a course supported by teaching assistants, the one-on-one attention I offer could be extended to hundreds of students.
MATLAB is ideal for this approach. The getting started videos on mathworks.com are very well done and perfect for learning the basics of MATLAB. I didn't see any materials on mathworks.com that I felt I could improve upon, so I just kept them. As the MathWorks tutorials became more advanced, I created my own screencasts on the new concepts covered each week, which the students watch before coming to class. Further support is available via the MATLAB doc command, which enables the students to get information on any MATLAB capability directly from the command prompt. Students found it empowering to discover that they did not need to be told what to type—they could learn whatever they wanted by using doc and experimenting on their own.
I use exercises and examples from Cleve Moler's online textbook Experiments with MATLAB. Otherwise, there is no required textbook for CMP 150. Instead, I recommend that the students acquire MATLAB and Simulink Student Version. I point out that this is an investment that they will use throughout their undergraduate years.
Easing into MATLAB
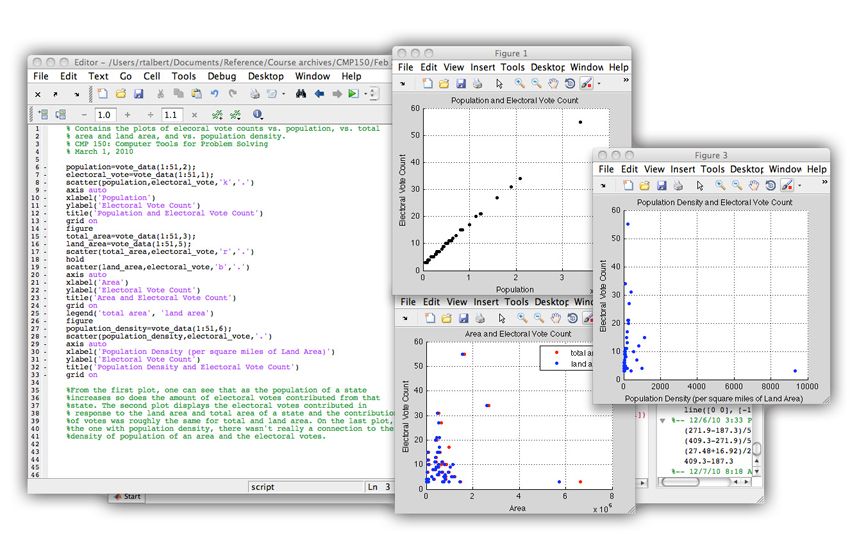
At first, the students find computer programming concepts difficult to grasp. I begin the course with topics that they can relate to immediately, using real-world data to make them more interesting and compelling. Because most students are familiar with plotting, and plotting and visualizing data is a great strength of MATLAB, I begin with that (Figure 2).
The students analyze data downloaded from the Indiana Department of Transportation and other online sources. In one exercise, they work with a large data set that includes the average price of gasoline for each month for more than 25 years. The data is in a matrix form, with months as the columns and years as the rows. To create plots, the students have to learn how to manipulate the data. This exercise serves as an excellent introduction to MATLAB matrix operations. The students create a MATLAB script that uses the reshape function to access price data for different months and generates a graph of those prices. They then use these graphs to draw conclusions about the data.
The next section of the course deals with statistical plotting, regression analysis, and curve fitting. The students are familiar with some of these topics from their calculus course, where they use a spreadsheet to perform regression. They quickly learn that MATLAB is much more powerful than a spreadsheet for this kind of work, providing more precision and greater control over the polynomial coefficients.
Experimentation and Symbolic Math
When the students are comfortable with the MATLAB environment and have some experience with plotting, using variables, and running scripts, I introduce basic programming constructs, including conditionals and loops. Although programming is entirely new to most of the students, I encourage them to experiment. Making mistakes and correcting them is an excellent way to learn a new skill.
In one assignment, students write a simple program that takes a numeric grade and produces the corresponding letter grade. A grade of 91, for example, generates an A-. I don't lead the students to a particular solution; I let them devise their own. Some gravitate to a series of if conditionals; others opt for a switch statement. When we discuss their solutions in class, they see that there are many ways of solving the same problem in MATLAB.
Toward the end of the course, the students use Symbolic Math Toolbox to solve problems symbolically. This past semester, a colleague who teaches Calculus 2 told me that some of his students were struggling with infinite series. As a result of that conversation, I changed my plans for the next week. I showed my class how to calculate the partial sum of a series numerically using a MATLAB script and then asked them to solve the same problem symbolically using the MuPAD notebook interface, which is included with Symbolic Math Toolbox. This exercise not only helped them understand the mathematical concepts they were struggling with; it also provided an excellent example of how they could apply MATLAB and Symbolic Math Toolbox in their coursework outside CMP 150.
Final Exams and Beyond
For the final exam, students must demonstrate competency in four areas: graphing and visualization, working with data, mathematical analysis, and programming. They have two hours to solve one problem in each of these categories using MATLAB. One of the programming problems asked them to create a function to approximate values of ex using a Taylor polynomial. Another option was to write a script that generates the first N numbers in the Fibonacci sequence, where N is an integer input to the script. I was pleased with the students' exam performance; it showed that they had come a long way in just 14 weeks.
We continue to integrate MATLAB into the rest of the curriculum. Students already use MATLAB in Calculus 3, and I'm working with colleagues in the science and business departments to increase their use of MATLAB. Student feedback has been positive. A few students who've taken a subsequent programming class in C++ have told me how much they miss programming in MATLAB. Many students say that the most valuable part of the course was learning how to tackle a new concept by themselves— how to find documentation or another source of information and stick with it until they understand it.
Thinking critically and acquiring and making sense of information are core intellectual skills in a liberal arts education. MATLAB is an excellent environment for students to develop and hone these skills early in their college careers.
Published 2011 - 91906v00