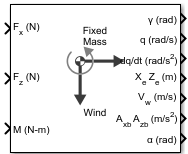
3DOF (Wind Axes)
Implement three-degrees-of-freedom equations of motion with respect to wind axes
Libraries:
Aerospace Blockset /
Equations of Motion /
3DOF
Description
The 3DOF (Wind Axes) block implements three-degrees-of-freedom equations of motion with respect to wind axes. It considers the rotation in the vertical plane of a wind-fixed coordinate frame about a flat Earth reference frame. For more information about the rotation and equations of motion, see Algorithms.
Limitations
The block assumes that the applied forces act at the center of gravity of the body, and that the mass and inertia are constant.
Ports
Input
Fx — Applied force along wind x-axis
scalar
Applied force along the wind x-axis, specified as a scalar, in the units selected in Units.
Data Types: double
Fz — Applied force along wind z-axis
scalar
Applied force along the wind z-axis, specified as a scalar.
Data Types: double
M — Applied pitching moment
scalar
Applied pitching moment, specified as a scalar.
Data Types: double
g — Gravity
scalar
Gravity, specified as a scalar.
Dependencies
To enable this port, set Gravity source to
External.
Data Types: double
Output
γ — Flight path angle
scalar
Flight path angle, within ±pi, returned as a scalar, in radians.
Data Types: double
q — Pitch angular rate
scalar
Pitch angular rate, returned as a scalar, in radians per second.
Data Types: double
dq/dt — Pitch angular acceleration
scalar
Pitch angular acceleration, returned as a scalar, in radians per second squared.
Data Types: double
XeZe — Location of body
two-element vector
Location of the body in the flat Earth reference frame, (Xe, Ze), returned as a two-element vector.
Data Types: double
Vw — Velocity in wind-fixed frame
two-element vector
Velocity of the body resolved into the wind-fixed coordinate frame, (V, 0), returned as a two-element vector.
Data Types: double
AxbAzb — Acceleration of body
two-element vector
Acceleration of the body with respect to the body-fixed coordinate frame, (Ax, Az), returned as a two-element vector.
Data Types: double
α — Angle of attack
scalar
Angle of attack, returned as a scalar, in radians.
Data Types: double
AxeAze — Acceleration of body
two-element vector
Accelerations of the body with respect to the inertial (flat Earth) coordinate frame, returned as a two-element vector. You typically connect this signal to the accelerometer.
Dependencies
To enable this port, select the Include inertial acceleration check box.
Data Types: double
Parameters
Main
Units — Input and output units
Metric (MKS) (default) | English (Velocity in ft/s) | English (Velocity in kts)
Input and output units, specified as Metric (MKS), English (Velocity in ft/s), or English (Velocity in kts).
| Units | Forces | Moment | Acceleration | Velocity | Position | Mass | Inertia |
|---|---|---|---|---|---|---|---|
Metric (MKS) | Newton | Newton-meter | Meters per second squared | Meters per second | Meters | Kilogram | Kilogram meter squared |
English (Velocity in ft/s) | Pound | Foot-pound | Feet per second squared | Feet per second | Feet | Slug | Slug foot squared |
English (Velocity in kts) | Pound | Foot-pound | Feet per second squared | Knots | Feet | Slug | Slug foot squared |
Programmatic Use
Block Parameter:
units |
| Type: character vector |
Values: Metric (MKS) | English (Velocity in ft/s) | English (Velocity in kts) |
Default: Metric (MKS) |
Axes — Body or wind axes
Wind (default) | Body
Body or wind axes, specified as Wind or
Body
Programmatic Use
Block Parameter:
axes |
| Type: character vector |
Values:
Wind | Body |
Default:
Wind |
Mass type — Mass type
Fixed (default) | Simple Variable | Custom Variable
Mass type, specified according to the following table.
| Mass Type | Description | Default for |
|---|---|---|
Fixed | Mass is constant throughout the simulation. | |
Simple Variable | Mass and inertia vary linearly as a function of mass rate. | |
Custom Variable | Mass and inertia variations are customizable. |
The Fixed selection conforms to the previously
described equations of motion.
Programmatic Use
Block Parameter:
mtype |
| Type: character vector |
Values:
Fixed | Simple Variable |
Custom Variable |
Default:
'Fixed' |
Initial airspeed — Initial speed
100 (default) | scalar greater than 0
Initial speed of the body,
(V0), specified as a
scalar greater than 0.
Programmatic Use
Block Parameter:
V_ini |
| Type: character vector |
Values:
'100' | scalar |
Default:
'100' |
Initial flight path angle — Initial flight path angle
0 (default) | scalar
Initial flight path angle of the body, (γ0), specified as a scalar.
Programmatic Use
Block Parameter: gamma_ini |
| Type: character vector |
Values:
'0' | scalar |
Default: '0' |
Initial body rotation rate — Initial pitch rotation rate
0 (default) | scalar
Initial pitch rotation rate, (q0), specified as a scalar.
Programmatic Use
Block
Parameter:
q_ini |
| Type: character vector |
Values:
'0' | scalar |
Default:
'0' |
Initial incidence — Initial angle
0 (default) | scalar
Initial angle between the velocity vector and the body, (α0), specified as a scalar.
Programmatic Use
Block Parameter: alpha_ini |
| Type: character vector |
Values:
'0' | scalar |
Default: '0' |
Initial position (x,z) — Initial location
[0 0] (default) | two-element vector
Initial location of the body in the flat Earth reference frame, specified as a two-element vector.
Programmatic Use
Block Parameter:
pos_ini |
| Type: character vector |
Values:
'[0 0]' | two-element vector |
Default:
'[0 0]' |
Initial mass — Initial mass
1.0 (default) | scalar
Initial mass of the rigid body, specified as a scalar.
Programmatic Use
Block Parameter: mass |
| Type: character vector |
Values:
'1.0' | scalar |
Default:
'1.0' |
Inertia body axes — Inertia of body
1.0 (default) | scalar
Inertia of the body, specified as a scalar.
Dependencies
To enable this parameter, set Mass type to Fixed.
Programmatic Use
Block Parameter: Iyy |
| Type: character vector |
Values:
'1.0' | scalar |
Default:
'1.0' |
Gravity Source — Gravity source
Internal (default) | External
Gravity source, specified as:
External | Variable gravity input to block |
Internal | Constant gravity specified in mask |
Programmatic Use
Block Parameter: g_in |
| Type: character vector |
Values: 'Internal' | 'External' |
Default: 'Internal' |
Acceleration due to gravity — Gravity source
9.81 (default) | scalar
Acceleration due to gravity, specified as a double scalar and used if internal gravity source
is selected. If gravity is to be neglected in the simulation, this value can be set to
0.
Dependencies
To enable this parameter, set Gravity Source to
Internal.
Programmatic Use
Block Parameter: g |
| Type: character vector |
Values:
'9.81' | scalar |
Default: '9.81' |
Include inertial acceleration — Include inertial acceleration port
off (default) | on
Select this check box to add an inertial acceleration in flat Earth frame output port. You typically connect this signal to the accelerometer.
Dependencies
To enable the AxeAze port, select this parameter.
Programmatic Use
Block Parameter: abi_flag |
| Type: character vector |
Values:
'off' |
'on' |
Default:
'off' |
State Attributes
Assign a unique name to each state. You can use state names instead of block paths during linearization.
The number of names must match the number of states, as shown for each item, or be empty. Set all or none of the block states.
To assign names to single-variable states, enter unique names between quotes, for example,
'q'or"q".To assign names to two-variable states, enter a comma-separated list surrounded by braces, for example,
{'Xe','Ze'}.If a state parameter is empty (
' '), no name is assigned.To assign state names with a variable in the MATLAB® workspace, enter the variable without quotes. A variable can be a character vector, cell array of character vectors, or string.
Velocity: e.g., 'V' — Velocity state name
'' (default) | character vector
Velocity state name, specified as a character vector or string.
Programmatic Use
Block Parameter: V_statename |
| Type: character vector | string |
Values:
'' | scalar |
Default: '' |
Position: e.g., {'Xe', 'Ze'} — Position state name
'' (default) | comma-separated list surrounded by braces
Position state names, specified as a comma-separated list surrounded by braces.
Programmatic Use
Block Parameter: pos_statename |
| Type: character vector |
Values:
'' | comma-separated list surrounded by braces |
Default: '' |
Body rotation rate: e.g., 'q' — Body rotation state name
'' (default) | scalar
Body rotation rate state names, specified as a character vector or string.
Programmatic Use
Block Parameter: q_statename |
| Type: character vector | string |
Values:
'' | scalar |
Default: '' |
Flight path angle: e.g., 'gamma' — Flight path angle state name
'' (default)
Flight path angle state name, specified as a character vector or string.
Programmatic Use
Block Parameter: gamma_statename |
| Type: character vector | string |
Values:
'' | scalar |
Default: '' |
Incidence angle e.g., 'alpha' — Incidence angle state name
'' (default) | scalar
Incidence angle state name, specified as a character vector or string.
Programmatic Use
Block
Parameter:
alpha_statename |
| Type: character vector | string |
Values:
'' | scalar |
Default:
'' |
Algorithms
The block considers the rotation in the vertical plane of a wind-fixed coordinate frame about a flat Earth reference frame.
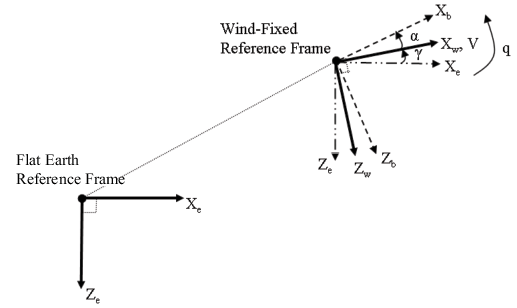
The equations of motion are
where the applied forces are assumed to act at the center of gravity of the body. Input variables are wind-axes forces Fx and Fz and body moment My. g is an optional input variable.
References
[1] Stevens, Brian, and Frank Lewis. Aircraft Control and Simulation. New York: John Wiley & Sons, 1992.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
Version History
Introduced in R2006aR2021b: 3DOF (Wind Axes) Block Changes
The 3DOF equations of motion have been updated. Existing models created prior to R2021b that contain 3DOF equations of motion blocks continue to run. If you replace a pre-R2021b version of a 3DOF equation of motion block with an R2021b or later version, your updated model might have a higher tendency for algebraic loops. For an example of how to remove algebraic loops using unit delays, see Remove Algebraic Loops. For further information about algebraic loops, see Identify Algebraic Loops in Your Model.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)