6th Order Point Mass Forces (Coordinated Flight)
Calculate forces used by sixth-order point mass in coordinated flight
Libraries:
Aerospace Blockset /
Equations of Motion /
Point Mass
Description
The 6th Order Point Mass Forces (Coordinated Flight) block calculates the applied forces for a single point mass or multiple point masses. For more information on the system for the applied forces, see Algorithms.
Limitations
The block assumes that there is fully coordinated flight, i.e., there is no side force (wind axes) and sideslip is always zero.
The flat Earth reference frame is considered inertial, an approximation that allows the forces due to the Earth motion relative to the "fixed stars" to be neglected.
Ports
Input
Output
Algorithms
This figure shows the applied forces in the system used by this block.
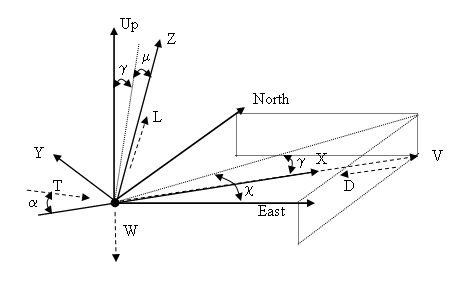
The applied forces [FxFyFh]T are in a system is defined by x-axis in the direction of vehicle velocity relative to air, z-axis is upwards and y-axis completes the right-handed frame and are functions of lift (L), drag (D), thrust (T), weight (W), flight path angle (γ), angle of attack (α), and bank angle (μ).
Extended Capabilities
Version History
Introduced before R2006a


