Control
Simulate various controllers, such as one-dimensional,
two-dimensional, three-dimensional types
Investigate the effects of implementation architecture on your design. Forms include predefined state-space controller blocks for one-, two-, and three-dimensional gain scheduling; linear interpolation; observer- and self-conditioned forms; and one-, two-, and three-dimensional matrix interpolation.
Blocks
| 1D Controller [A(v),B(v),C(v),D(v)] | Implement gain-scheduled state-space controller depending on one scheduling parameter |
| 1D Controller Blend u=(1-L).K1.y+L.K2.y | Implement 1-D vector of state-space controllers by linear interpolation of their outputs |
| 1D Observer Form [A(v),B(v),C(v),F(v),H(v)] | Implement gain-scheduled state-space controller in observer form depending on one scheduling parameter |
| 1D Self-Conditioned [A(v),B(v),C(v),D(v)] | Implement gain-scheduled state-space controller in self-conditioned form depending on one scheduling parameter |
| 2D Controller [A(v),B(v),C(v),D(v)] | Implement gain-scheduled state-space controller depending on two scheduling parameters |
| 2D Controller Blend | Implement 2-D vector of state-space controllers by linear interpolation of their outputs |
| 2D Observer Form [A(v),B(v),C(v),F(v),H(v)] | Implement gain-scheduled state-space controller in observer form depending on two scheduling parameters |
| 2D Self-Conditioned [A(v),B(v),C(v),D(v)] | Implement gain-scheduled state-space controller in self-conditioned form depending on two scheduling parameters |
| 3D Controller [A(v),B(v),C(v),D(v)] | Implement gain-scheduled state-space controller depending on three scheduling parameters |
| 3D Observer Form [A(v),B(v),C(v),F(v),H(v)] | Implement gain-scheduled state-space controller in observer form depending on three scheduling parameters |
| 3D Self-Conditioned [A(v),B(v),C(v),D(v)] | Implement gain-scheduled state-space controller in self-conditioned form depending on two scheduling parameters |
| Gain Scheduled Lead-Lag | Implement first-order lead-lag with gain-scheduled coefficients |
| Interpolate Matrix(x) | Return interpolated matrix for given input |
| Interpolate Matrix(x,y) | Return interpolated matrix for given inputs |
| Interpolate Matrix(x,y,z) | Return interpolated matrix for given inputs |
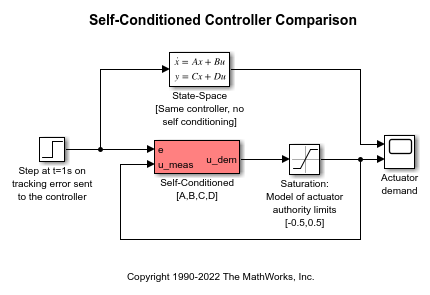
| Self-Conditioned [A,B,C,D] | Implement state-space controller in self-conditioned form |