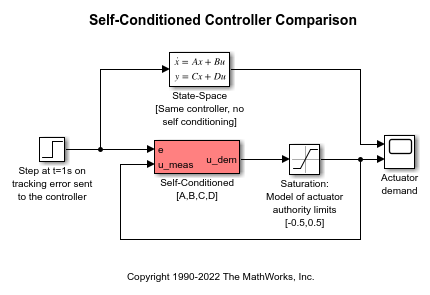
Self-Conditioned [A,B,C,D]
Implement state-space controller in self-conditioned form
Libraries:
Aerospace Blockset /
GNC /
Control
Description
The Self-Conditioned [A,B,C,D] block can be used to implement the state-space controller defined by
in the self-conditioned form
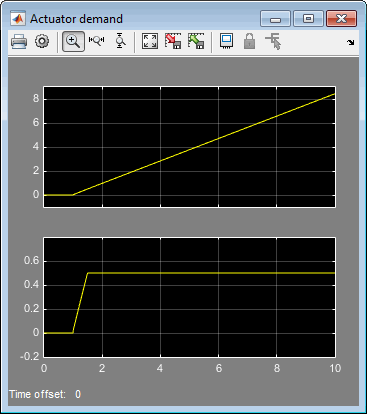
The input is a vector of the achieved actuator positions, and the output is the vector of controller actuator demands. In the case that the actuators are not limited, then and substituting the output equation into the state equation returns the nominal controller. In the case that they are not equal, the dynamics of the controller are set by the poles of A-HC.
Hence H must be chosen to make the poles
sufficiently fast to track but
at the same time not so fast that noise on e is propagated to . The matrix H is
designed by a callback to the Control System Toolbox™ command place to place the poles at defined locations.
Limitations
This block requires the Control System Toolbox license.
Ports
Input
Output
Parameters
More About
References
[1] Kautsky, Nichols, and Van Dooren, "Robust Pole Assignment in Linear State Feedback," International Journal of Control, Vol. 41, Number 5, 1985, pp. 1129-1155.
Extended Capabilities
Version History
Introduced before R2006a