Gene Expression Profile Analysis
This example shows a number of ways to look for patterns in gene expression profiles.
Exploring the Data Set
This example uses data from the microarray study of gene expression in yeast published by DeRisi, et al. 1997 [1]. The authors used DNA microarrays to study temporal gene expression of almost all genes in Saccharomyces cerevisiae during the metabolic shift from fermentation to respiration. Expression levels were measured at seven time points during the diauxic shift. The full data set can be downloaded from the Gene Expression Omnibus website, https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=GSE28.
The MAT-file yeastdata.mat contains the expression values (log2 of ratio of CH2DN_MEAN and CH1DN_MEAN) from the seven time steps in the experiment, the names of the genes, and an array of the times at which the expression levels were measured.
load yeastdata.mat
To get an idea of the size of the data you can use numel(genes) to show how many genes are included in the data set.
numel(genes)
ans =
6400
You can access the genes names associated with the experiment by indexing the variable genes, a cell array representing the gene names. For example, the 15th element in genes is YAL054C. This indicates that the 15th row of the variable yeastvalues contains expression levels for YAL054C.
genes{15}
ans =
'YAL054C'
A simple plot can be used to show the expression profile for this ORF.
plot(times, yeastvalues(15,:)) xlabel('Time (Hours)'); ylabel('Log2 Relative Expression Level');
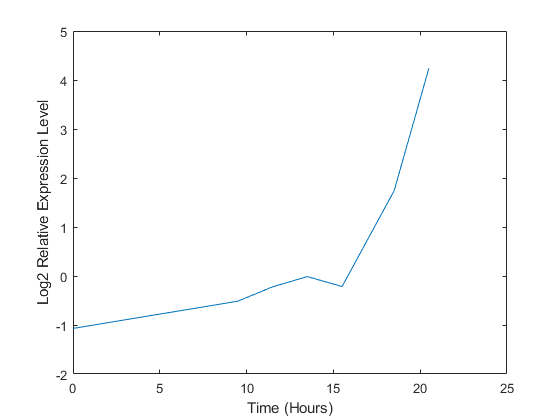
You can also plot the actual expression ratios, rather than the log2-transformed values.
plot(times, 2.^yeastvalues(15,:)) xlabel('Time (Hours)'); ylabel('Relative Expression Level');
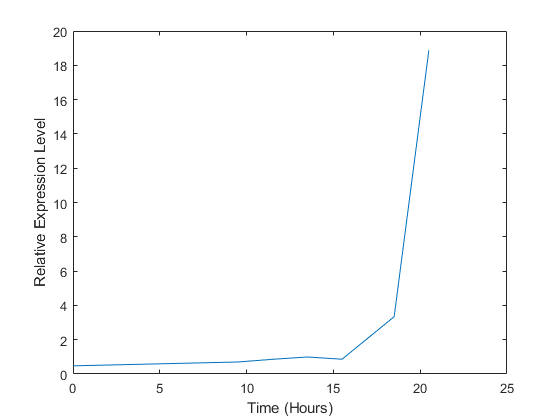
The gene associated with this ORF, ACS1, appears to be strongly up-regulated during the diauxic shift. You can compare the expression of this gene to the expression of other genes by plotting multiple lines on the same figure.
hold on plot(times, 2.^yeastvalues(16:26,:)') xlabel('Time (Hours)'); ylabel('Relative Expression Level'); title('Profile Expression Levels');
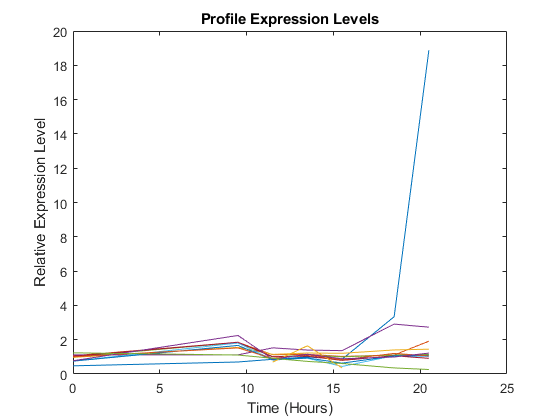
Filtering the Genes
Typically, a gene expression dataset includes information corresponding to genes that do not show any interesting changes during the experiment. To make it easier to find the interesting genes, you can reduce the size of the data set to some subset that contains only the most significant genes.
If you look through the gene list, you will see several spots marked as 'EMPTY'. These are empty spots on the array, and while they might have data associated with them, for the purposes of this example, you can consider these points to be noise. These points can be found using the strcmp function and removed from the data set with indexing commands.
emptySpots = strcmp('EMPTY',genes);
yeastvalues(emptySpots,:) = [];
genes(emptySpots) = [];
numel(genes)
ans =
6314
There are also see several places in the dataset where the expression level is marked as NaN. This indicates that no data was collected for this spot at the particular time step. One approach to dealing with these missing values would be to impute them using the mean or median of data for the particular gene over time. This example uses a less rigorous approach of simply throwing away the data for any genes where one or more expression level was not measured. The function isnan is used to identify the genes with missing data and indexing commands are used to remove the genes with missing data.
nanIndices = any(isnan(yeastvalues),2); yeastvalues(nanIndices,:) = []; genes(nanIndices) = []; numel(genes)
ans =
6276
If you were to plot the expression profiles of all the remaining profiles, you would see that most profiles are flat and not significantly different from the others. This flat data is obviously of use as it indicates that the genes associated with these profiles are not significantly affected by the diauxic shift; however, in this example, you are interested in the genes with large changes in expression accompanying the diauxic shift. You can use filtering functions in the Bioinformatics Toolbox™ to remove genes with various types of profiles that do not provide useful information about genes affected by the metabolic change.
You can use the genevarfilter function to filter out genes with small variance over time. The function returns a logical array (i.e., a mask) of the same size as the variable genes with ones corresponding to rows of yeastvalues with variance greater than the 10th percentile and zeros corresponding to those below the threshold. You can use the mask to index into the values and remove the filtered genes.
mask = genevarfilter(yeastvalues); yeastvalues = yeastvalues(mask,:); genes = genes(mask); numel(genes)
ans =
5648
The function genelowvalfilter removes genes that have very low absolute expression values. Note that these filter functions can also automatically calculate the filtered data and names, so it is not necessary to index the original data using the mask.
[mask,yeastvalues,genes] = genelowvalfilter(yeastvalues,genes,'absval',log2(3));
numel(genes)
ans = 822
Finally, you can use the function geneentropyfilter to remove genes whose profiles have low entropy, for example entropy levels in the 15th percentile of the data.
[mask,yeastvalues,genes] = geneentropyfilter(yeastvalues,genes,'prctile',15);
numel(genes)
ans = 614
Cluster Analysis
Now that you have a manageable list of genes, you can look for relationships between the profiles using some different clustering techniques from the Statistics and Machine Learning Toolbox™. For hierarchical clustering, the function pdist calculates the pairwise distances between profiles and linkage creates the hierarchical cluster tree.
corrDist = pdist(yeastvalues,'corr'); clusterTree = linkage(corrDist,'average');
The cluster function calculates the clusters based on either a cutoff distance or a maximum number of clusters. In this case, the maxclust option is used to identify 16 distinct clusters.
clusters = cluster(clusterTree,'maxclust',16);
The profiles of the genes in these clusters can be plotted together using a simple loop and the subplot command.
figure for c = 1:16 subplot(4,4,c); plot(times,yeastvalues((clusters == c),:)'); axis tight end sgtitle('Hierarchical Clustering of Profiles');
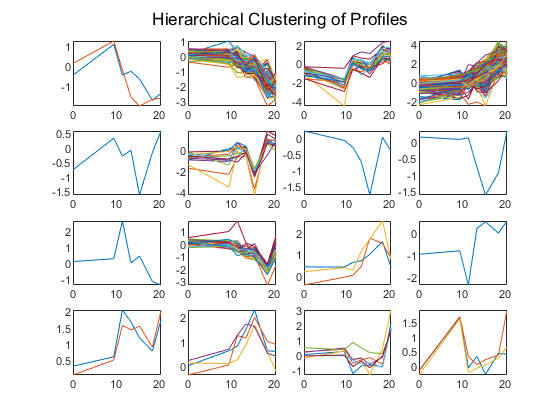
The Statistics and Machine Learning Toolbox also has a K-means clustering function. Again, sixteen clusters are found, but because the algorithm is different these will not necessarily be the same clusters as those found by hierarchical clustering.
Initialize the state of the random number generator to ensure that the figures generated by these command match the figures in the HTML version of this example.
rng('default'); [cidx, ctrs] = kmeans(yeastvalues,16,'dist','corr','rep',5,'disp','final'); figure for c = 1:16 subplot(4,4,c); plot(times,yeastvalues((cidx == c),:)'); axis tight end sgtitle('K-Means Clustering of Profiles');
Replicate 1, 21 iterations, total sum of distances = 23.4699. Replicate 2, 22 iterations, total sum of distances = 23.5615. Replicate 3, 10 iterations, total sum of distances = 24.823. Replicate 4, 28 iterations, total sum of distances = 23.4501. Replicate 5, 19 iterations, total sum of distances = 23.5109. Best total sum of distances = 23.4501
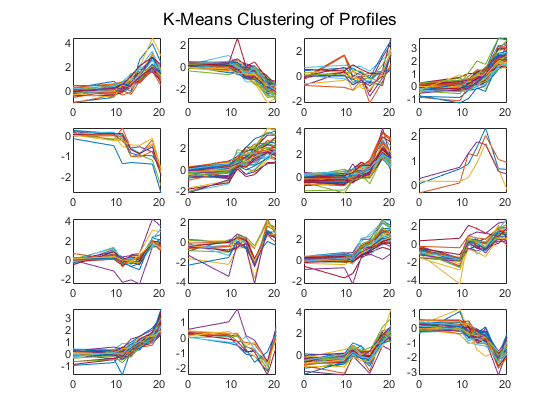
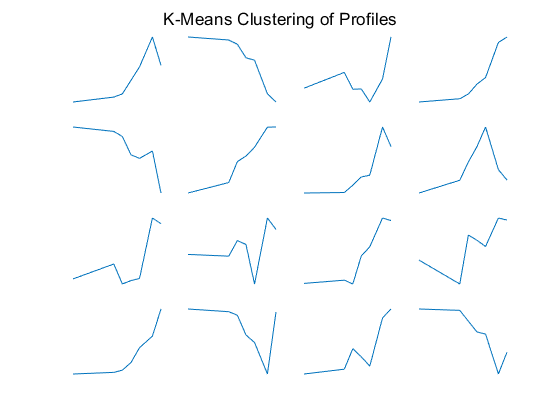
Instead of plotting all the profiles, you can plot just the centroids.
figure for c = 1:16 subplot(4,4,c); plot(times,ctrs(c,:)'); axis tight axis off end sgtitle('K-Means Clustering of Profiles');
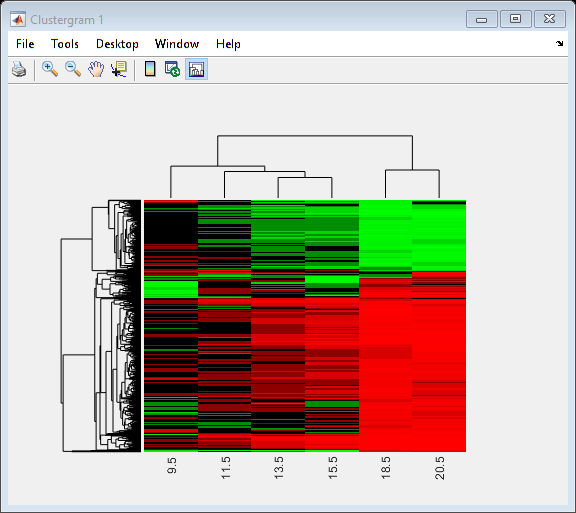
You can use the clustergram function to create a heat map of the expression levels and a dendrogram from the output of the hierarchical clustering.
cgObj = clustergram(yeastvalues(:,2:end),'RowLabels',genes,'ColumnLabels',times(2:end));
Principal Component Analysis
Principal-component analysis(PCA) is a useful technique that can be used to reduce the dimensionality of large data sets, such as those from microarrays. PCA can also be used to find signals in noisy data. The function mapcaplot calculates the principal components of a data set and create scatter plots of the results. You can interactively select data points from one of the plots, and these points are automatically highlighted in the other plot. This lets you visualize multiple dimensions simultaneously.
h = mapcaplot(yeastvalues,genes);
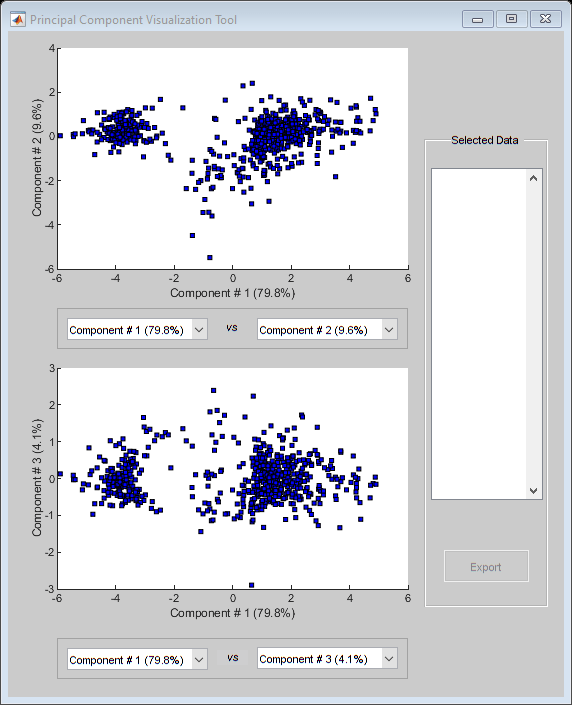
Notice that the scatter plot of the scores of the first two principal components shows that there are two distinct regions. This is not unexpected as the filtering process removed many of the genes with low variance or low information. These genes would have appeared in the middle of the scatter plot.
If you want to look at the values of the principal components, the pca function in the Statistics and Machine Learning Toolbox is used to calculate the principal components of a data set.
[pc, zscores, pcvars] = pca(yeastvalues);
The first output, pc, is a matrix of the principal components of the yeastvalues data. The first column of the matrix is the first principal component, the second column is the second principal component, and so on. The second output, zscores, consists of the principal component scores, i.e., a representation of yeastvalues in the principal component space. The third output, pcvars, contains the principal component variances, which give a measure of how much of the variance of the data is accounted for by each of the principal components.
It is clear that the first principal component accounts for a majority of the variance in the model. You can compute the exact percentage of the variance accounted for by each component as shown below.
pcvars./sum(pcvars) * 100
ans =
79.8316
9.5858
4.0781
2.6486
2.1723
0.9747
0.7089
This means that almost 90% of the variance is accounted for by the first two principal components. You can use the cumsum command to see the cumulative sum of the variances.
cumsum(pcvars./sum(pcvars) * 100)
ans = 79.8316 89.4174 93.4955 96.1441 98.3164 99.2911 100.0000
If you want to have more control over the plotting of the principal components, you can use the scatter function.
figure scatter(zscores(:,1),zscores(:,2)); xlabel('First Principal Component'); ylabel('Second Principal Component'); title('Principal Component Scatter Plot');
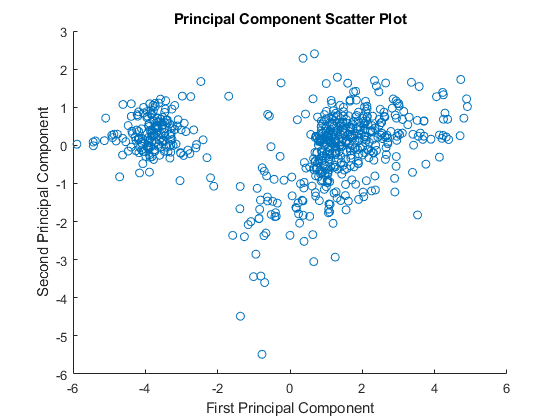
An alternative way to create a scatter plot is with the function gscatter from the Statistics and Machine Learning Toolbox. gscatter creates a grouped scatter plot where points from each group have a different color or marker. You can use clusterdata, or any other clustering function, to group the points.
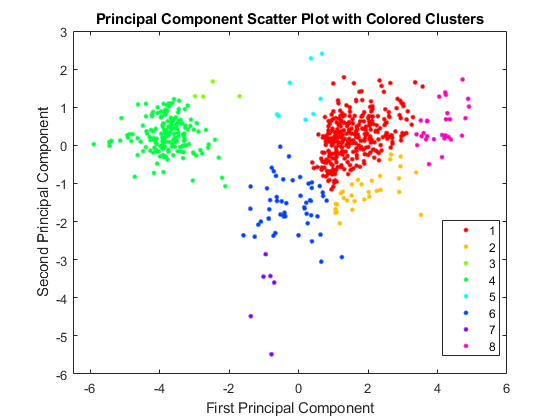
figure pcclusters = clusterdata(zscores(:,1:2),'maxclust',8,'linkage','av'); gscatter(zscores(:,1),zscores(:,2),pcclusters,hsv(8)) xlabel('First Principal Component'); ylabel('Second Principal Component'); title('Principal Component Scatter Plot with Colored Clusters');
Self-Organizing Maps
If you have the Deep Learning Toolbox™, you can use a self-organizing map (SOM) to cluster the data.
% Check to see if the Deep Learning Toolbox is installed if ~exist(which('selforgmap'),'file') disp('The Self-Organizing Maps section of this example requires the Deep Learning Toolbox.') return end
The selforgmap function creates a new SOM network object. This example will generate a SOM using the first two principal components.
P = zscores(:,1:2)'; net = selforgmap([4 4]);
Train the network using the default parameters.
net = train(net,P);
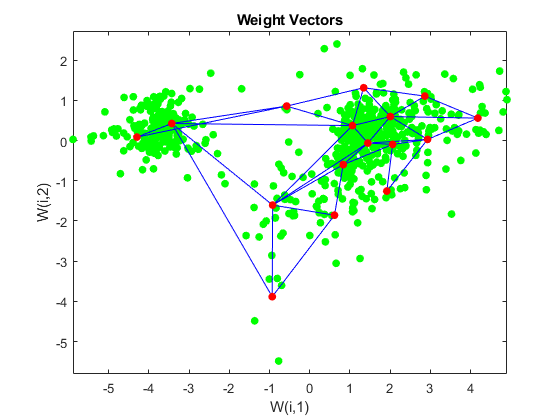
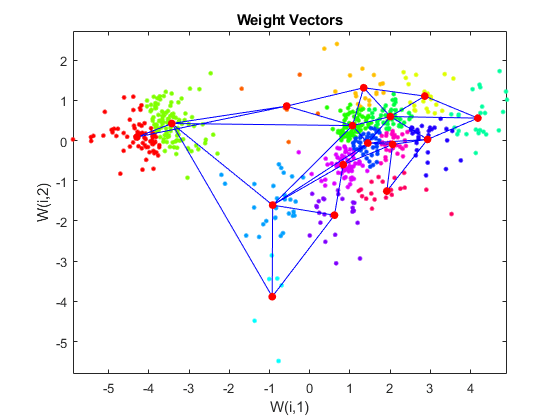
Use plotsom to display the network over a scatter plot of the data. Note that the SOM algorithm uses random starting points so the results will vary from run to run.
figure plot(P(1,:),P(2,:),'.g','markersize',20) hold on plotsom(net.iw{1,1},net.layers{1}.distances) hold off
You can assign clusters using the SOM by finding the nearest node to each point in the data set.
distances = dist(P',net.IW{1}');
[d,cndx] = min(distances,[],2); % cndx contains the cluster index
figure
gscatter(P(1,:),P(2,:),cndx,hsv(numel(unique(cndx)))); legend off;
hold on
plotsom(net.iw{1,1},net.layers{1}.distances);
hold off
Close all figures.
close('all');
delete(cgObj);
delete(h);
References
[1] DeRisi, J.L., Iyer, V.R. and Brown, P.O., "Exploring the metabolic and genetic control of gene expression on a genomic scale", Science, 278(5338):680-6, 1997.
