Raised Cosine Filtering
This example shows the intersymbol interference (ISI) rejection capability of the raised cosine filter, and how to split the raised cosine filtering between transmitter and receiver, using raised cosine transmit and receive filter System objects.
Raised Cosine Filter Specifications
The main parameter of a raised cosine filter is its roll-off factor, which indirectly specifies the bandwidth of the filter. Ideal raised cosine filters have an infinite number of taps. Therefore, practical raised cosine filters are windowed. The window length is controlled using the FilterSpanInSymbols property. In this example, you specify the window length as six symbol durations because the filter spans six symbol durations. Such a filter also has a group delay of three symbol durations. Raised cosine filters are used for pulse shaping, where the signal is upsampled. Therefore, we also need to specify the upsampling factor. These parameters are used to design the raised cosine filter for this example.
Nsym = 6; % Filter span in symbol durations beta = 0.5; % Roll-off factor sampsPerSym = 8; % Upsampling factor
Create a raised cosine transmit filter System object™ and set its properties to obtain the desired filter characteristics. Use impz to visualize filter characteristics.
rctFilt = comm.RaisedCosineTransmitFilter(... Shape='Normal', ... RolloffFactor=beta, ... FilterSpanInSymbols=Nsym, ... OutputSamplesPerSymbol=sampsPerSym)
rctFilt =
comm.RaisedCosineTransmitFilter with properties:
Shape: 'Normal'
RolloffFactor: 0.5000
FilterSpanInSymbols: 6
OutputSamplesPerSymbol: 8
Gain: 1
% Visualize the impulse response
impz(rctFilt.coeffs.Numerator)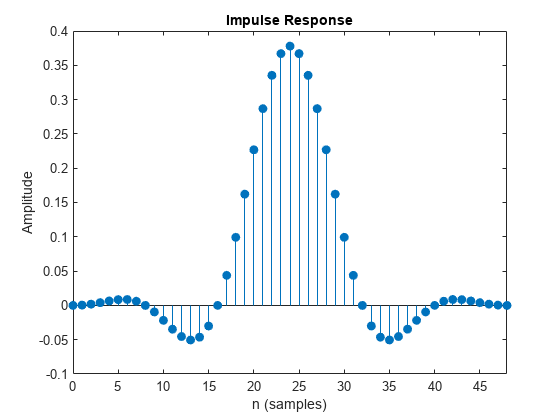
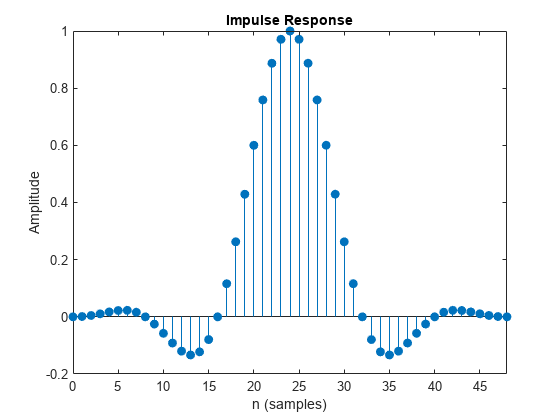
This object designs a direct-form polyphase FIR filter with unit energy. The filter has an order of Nsym*sampsPerSym, or Nsym*sampsPerSym+1 taps. You can utilize the Gain property to normalize the filter coefficients so that the filtered and unfiltered data matches when overlayed.
% Normalize to obtain maximum filter tap value of 1 b = coeffs(rctFilt); rctFilt.Gain = 1/max(b.Numerator); % Visualize the impulse response impz(rctFilt.coeffs.Numerator)
Pulse Shaping with Raised Cosine Filters
Generate a bipolar data sequence, and use the raised cosine filter to shape the waveform without introducing ISI.
% Parameters DataL = 20; % Data length in symbols R = 1000; % Data rate Fs = R * sampsPerSym; % Sampling frequency % Create a local random stream to be used by random number generators for % repeatability hStr = RandStream('mt19937ar',Seed=0); % Generate random data x = 2*randi(hStr,[0 1],DataL,1)-1; % Time vector sampled at symbol rate in milliseconds tx = 1000 * (0: DataL - 1) / R;
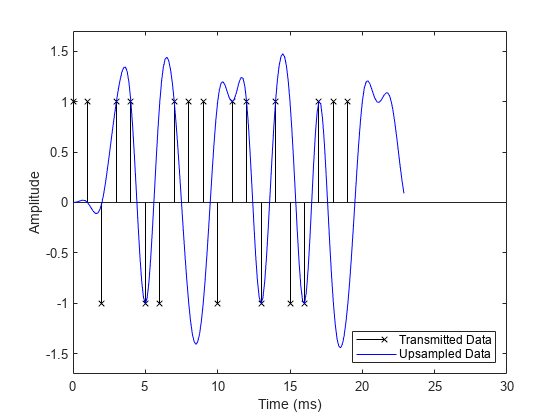
Compare the digital data and the interpolated signal in a plot. It is difficult to compare the two signals because the peak response of the filter is delayed by the group delay of the filter (Nsym/(2*R)). Note that we append Nsym/2 zeros at the end of input x to flush all the useful samples out of the filter.
% Filter yo = rctFilt([x; zeros(Nsym/2,1)]); % Time vector sampled at sampling frequency in milliseconds to = 1000 * (0: (DataL+Nsym/2)*sampsPerSym - 1) / Fs; % Plot data fig1 = figure; stem(tx, x, 'kx'); hold on; % Plot filtered data plot(to, yo, 'b-'); hold off; % Set axes and labels axis([0 30 -1.7 1.7]); xlabel('Time (ms)'); ylabel('Amplitude'); legend('Transmitted Data','Upsampled Data','Location','southeast')
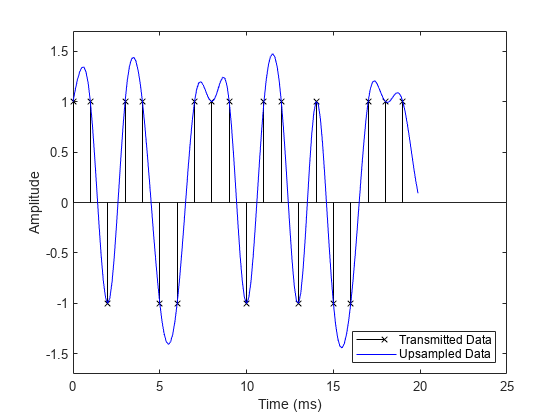
Compensate for the raised cosine filter group delay by delaying the input signal. Now it is easy to see how the raised cosine filter upsamples and filters the signal. The filtered signal is identical to the delayed input signal at the input sample times. This shows the raised cosine filter capability to band-limit the signal while avoiding ISI.
% Filter group delay, since raised cosine filter is linear phase and % symmetric. fltDelay = Nsym / (2*R); % Correct for propagation delay by removing filter transients yo = yo(fltDelay*Fs+1:end); to = 1000 * (0: DataL*sampsPerSym - 1) / Fs; % Plot data. stem(tx, x, 'kx'); hold on; % Plot filtered data. plot(to, yo, 'b-'); hold off; % Set axes and labels. axis([0 25 -1.7 1.7]); xlabel('Time (ms)'); ylabel('Amplitude'); legend('Transmitted Data','Upsampled Data','Location','southeast')
Roll-off Factor
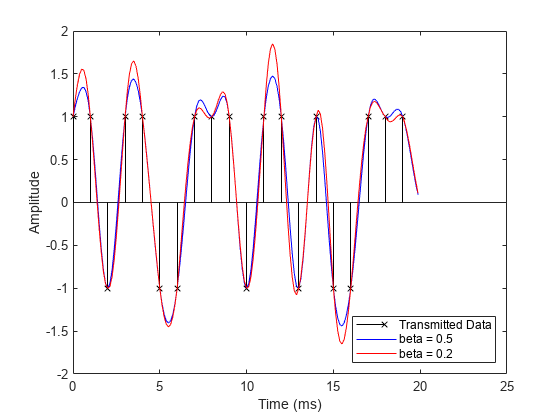
Show the effect that changing the roll-off factor from .5 (blue curve) to .2 (red curve) has on the resulting filtered output. The lower value for roll-off causes the filter to have a narrower transition band causing the filtered signal overshoot to be greater for the red curve than for the blue curve.
% Set roll-off factor to 0.2 rctFilt2 = comm.RaisedCosineTransmitFilter(... Shape='Normal', ... RolloffFactor=0.2, ... FilterSpanInSymbols=Nsym, ... OutputSamplesPerSymbol=sampsPerSym); % Normalize filter b = coeffs(rctFilt2); rctFilt2.Gain = 1/max(b.Numerator); % Filter yo1 = rctFilt2([x; zeros(Nsym/2,1)]); % Correct for propagation delay by removing filter transients yo1 = yo1(fltDelay*Fs+1:end); % Plot data stem(tx, x, 'kx'); hold on; % Plot filtered data plot(to, yo, 'b-',to, yo1, 'r-'); hold off; % Set axes and labels axis([0 25 -2 2]); xlabel('Time (ms)'); ylabel('Amplitude'); legend('Transmitted Data','beta = 0.5','beta = 0.2',... 'Location','southeast')
Square-Root Raised Cosine Filters
A typical use of raised cosine filtering is to split the filtering between transmitter and receiver. Both transmitter and receiver employ square-root raised cosine filters. The combination of transmitter and receiver filters is a raised cosine filter, which results in minimum ISI. We specify a square-root raised cosine filter by setting the shape as 'Square root'.
% Design raised cosine filter with given order in symbols rctFilt3 = comm.RaisedCosineTransmitFilter(... Shape='Square root', ... RolloffFactor=beta, ... FilterSpanInSymbols=Nsym, ... OutputSamplesPerSymbol=sampsPerSym);
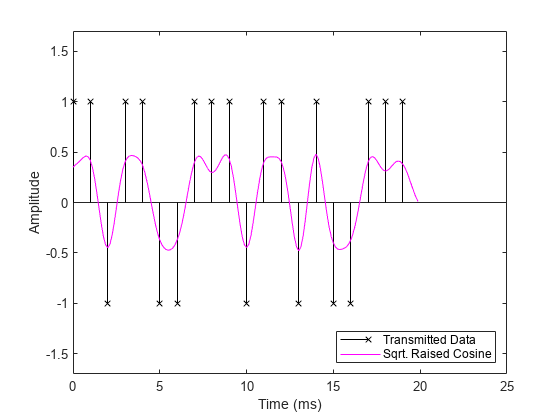
The data stream is upsampled and filtered at the transmitter using the designed filter. This plot shows the transmitted signal when filtered using the square-root raised cosine filter.
% Upsample and filter. yc = rctFilt3([x; zeros(Nsym/2,1)]); % Correct for propagation delay by removing filter transients yc = yc(fltDelay*Fs+1:end); % Plot data. stem(tx, x, 'kx'); hold on; % Plot filtered data. plot(to, yc, 'm-'); hold off; % Set axes and labels. axis([0 25 -1.7 1.7]); xlabel('Time (ms)'); ylabel('Amplitude'); legend('Transmitted Data','Sqrt. Raised Cosine','Location','southeast')
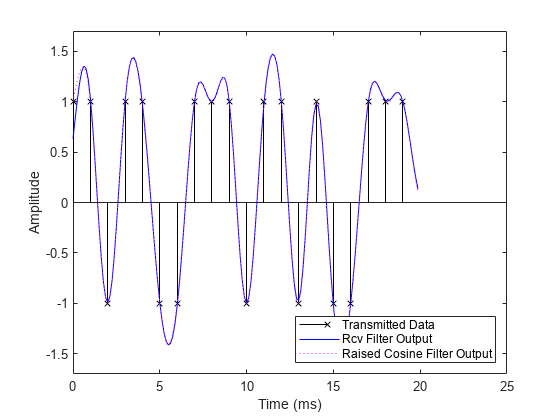
The transmitted signal (magenta curve) is then filtered at the receiver. We did not decimate the filter output to show the full waveform. The default unit energy normalization ensures that the gain of the combination of the transmit and receive filters is the same as the gain of a normalized raised cosine filter. The filtered received signal, which is virtually identical to the signal filtered using a single raised cosine filter, is depicted by the blue curve at the receiver.
% Design and normalize filter. rcrFilt = comm.RaisedCosineReceiveFilter(... 'Shape', 'Square root', ... 'RolloffFactor', beta, ... 'FilterSpanInSymbols', Nsym, ... 'InputSamplesPerSymbol', sampsPerSym, ... 'DecimationFactor', 1); % Filter at the receiver. yr = rcrFilt([yc; zeros(Nsym*sampsPerSym/2, 1)]); % Correct for propagation delay by removing filter transients yr = yr(fltDelay*Fs+1:end); % Plot data. stem(tx, x, 'kx'); hold on; % Plot filtered data. plot(to, yr, 'b-',to, yo, 'm:'); hold off; % Set axes and labels. axis([0 25 -1.7 1.7]); xlabel('Time (ms)'); ylabel('Amplitude'); legend('Transmitted Data','Rcv Filter Output', ... 'Raised Cosine Filter Output','Location','southeast')
Computational Cost
In the following table, we compare the computational cost of a polyphase FIR interpolation filter and polyphase FIR decimation filter.
C1 = cost(rctFilt3); C2 = cost(rcrFilt);
------------------------------------------------------------------------
Implementation Cost Comparison
------------------------------------------------------------------------
Multipliers Adders Mult/Symbol Add/Symbol
Multirate Interpolator 49 41 49 41
Multirate Decimator 49 48 6.125 6
