Binary-Input RS Encoder
Create Reed-Solomon code from binary vector data
Libraries:
Communications Toolbox /
Error Detection and Correction /
Block
Description
The Binary-Input RS Encoder block creates a Reed-Solomon code.
The symbols for the code are binary sequences of length M, corresponding to elements of the Galois field GF(2M). The first bit in each symbol is the most significant bit.
Suppose M = 3, N = 23-1 = 7, and K = 2. Then a message is a vector of length 2 whose entries are integers between 0 and 7. A corresponding codeword is a vector of length 7 whose entries are integers between 0 and 7. The following figure illustrates possible input and output signals to this block when codeword length N=7 and message word length K=2. Since N=2M–1, when N=7, the symbol length, M=3.
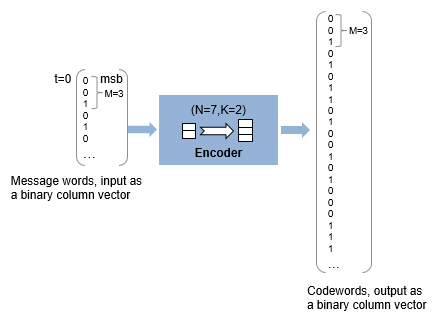
Each input message word is a binary vector of length 6, that represents 2 three-bit integers. Each corresponding output codeword is a binary vector of length 21 that represents 7 three-bit integers. For more information, see Input and Output Signal Length in RS Blocks.
Examples
Compute BER of Reed-Solomon Encoded Signal
Apply Reed-Solomon (RS) encoding and 2-FSK modulation to an integer-valued signal, pass the modulated signal through an AWGN channel. Compute the bit error rate (BER) of the signal after applying 2-FSK demodulation and binary output RS decoding.
The cm_binary_input_rs_encoder_output_decoder model includes the:
Random Integer Generator block — To generate an integer-valued signal
Data Type Conversion (Simulink) block — To convert data type to type expected for error rate computations
Binary-Input RS Encoder block — To RS encode the signal
M-FSK Modulator Baseband block — To 2-FSK-modulates the signal
AWGN Channel block — To add Gaussian white noise to the signal
M-FSK Demodulator Baseband block — To 2-FSK demodulate signal
Binary-Output RS Decoder block — To RS decode the signal
Two separate Error Rate Calculation blocks — To compute the error statistics for the signal before and after RS decoding

Compare the decoded and encoded error statistics to show error correction benefit for the received signal provided by the RS coding.
For an AWGN channel with SNR = -2 dB, the computed error rates are:
Decoded Encoded
_________ _______
BER 0.0004375 0.00235
Number of errors 21 141
Number of bits transmitted 48000 60000
Ports
Input
In — Message
binary column vector
Message in bits, specified as one of the following:
When there is no message shortening, a (NC×K×M)-by-1 binary column vector.
When there is message shortening, a (NC×S×M)-by-1 binary column vector.
NC is the number of message words, K is the Message length K (symbols), M is the number of bits per symbol, and S is the Shortened message length S (symbols).
Note
The number of decoded message words equals the number of codewords.
For more information, see Input and Output Signal Length in RS Blocks.
Data Types: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32 | Boolean | ufix(1)
Output
Out — Reed-Solomon codeword
binary column vector
Reed-Solomon codeword in bits, returned as an (NC×(N – K + S – P)×M)-by-1 binary column vector. NC is the number of codewords, N is the Codeword length N (symbols), K is the Message length K (symbols), S is the Shortened message length S (symbols), P is the number of punctures per codeword, and M is the number of bits per symbol.
For more information, see Input and Output Signal Length in RS Blocks.
Data Types: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32 | Boolean | ufix(1)
For more information, see Supported Data Types.
Parameters
To edit block parameters interactively, use the Property Inspector. From the Simulink® Toolstrip, on the Simulation tab, in the Prepare gallery, select Property Inspector.
Codeword length N (symbols) — Codeword length
7 (default) | integer
Codeword length in symbols, specified as an integer.
For more information, see Restrictions on the M and the Codeword Length N and Input and Output Signal Length in RS Blocks.
Message length K (symbols) — Message word length
3 (default) | integer
Message word length in symbols, specified as an integer in the range [1, N–2], where N is the codeword length.
Shortened message length S (symbols) — Shortened message word length
3 (default) | integer
Shortened message word length in symbols, specified as an integer, such that S ≤ K. When Shortened message length S (symbols) < Message length K (symbols), the Reed-Solomon code is shortened.
You still specify N and K values for the full-length (N, K) code but the decoding is shortened to an (N–K+S, S) code.
Dependencies
To enable this parameter, select Specify shortened message length.
Generator polynomial — Generator polynomial
rsgenpoly(7, 3, [], [],
'double') (default) | polynomial character vector | binary row vector | binary Galois row vector
Generator polynomial with values from 0 to 2M–1, in order of descending power, specified as one of the following:
A polynomial character vector. For more information, see Representation of Polynomials in Communications Toolbox.
An integer row vector that represents the coefficients of the generator polynomial in order of descending power.
An integer Galois row vector that represents the coefficients of the generator polynomial in order of descending power.
Each coefficient is an element of the Galois field defined by the primitive polynomial. For more information, see Specify the Generator Polynomial.
Example: [1 3 1 2 3], which is equivalent to
rsgenpoly(7,3)
Dependencies
To enable this parameter, select Specify generator polynomial.
Primitive polynomial — Primitive polynomial
'X^3 + X + 1' (default) | polynomial character vector | binary row vector
Primitive polynomial in order of descending power. This polynomial is of order M and defines the finite Galois field GF(2M) corresponding to the integers that form message words and codewords. Specify the primitive polynomial as one of the following:
A polynomial character vector. For more information, see Representation of Polynomials in Communications Toolbox.
A binary row vector that represents the coefficients of the generator polynomial.
For more information, see Restrictions on the M and the Codeword Length N.
Example: 'X^3 + X + 1', which is the primitive
polynomial used for a (7,3) code, ppoly = primpoly(3,'nodisplay');
int2bit(ppoly,ceil(log2(max(ppoly))))'
Dependencies
To enable this parameter, select Specify primitive polynomial.
Puncture vector — Puncture vector
[ones(2,1); zeros(2,1)] (default) | binary column vector
Puncture vector, specified as an
(N–K)-by-1 binary column vector.
Element indices with 1s represent data
symbol indices that pass through the block
unaltered. Element indices with 0s represent data
symbol indices that get punctured, or removed,
from the data stream. For more information, see Puncturing and Erasures.
Dependencies
To enable this parameter, select Puncture code.
Output data type — Output type of the block
Same as input (default) | boolean | double
Output type of the block, specified as Same as
input, boolean, or
double.
Block Characteristics
More About
Input and Output Signal Length in RS Blocks
The Reed-Solomon code has a message word length, K, or shortened message word length, S. The codeword length is N – K + S – P, where N is the full codeword length and P is the number of punctures per codeword. When there is no message shortening, the codeword length expression reduces to N – P, because K = S. If the decoder is processing multiple codewords per frame, then the same puncture pattern holds for all codewords.
This table provides expressions for the input and output signal lengths for the Reed-Solomon encoder and decoder.
The notation y = NC × x denotes that y is an integer multiple of x.
| Input, Erasure, and Output Vector Lengths | ||
|---|---|---|
| RS Block Coder | No Message Shortening Used | Message Shortening Used |
|
Binary-Input RS Encoder |
Input Length (bits): NC × K × M Output Length (bits): NC × (N–P) × M |
Input Length (bits): NC × S × M Output Length (bits): NC × (N–K+S–P) × M |
|
Binary-Output RS Decoder |
Input Length (bits): NC × (N–P) × M Erasures Length (symbols): NC × (N–P) Output Length (bits): NC × K × M |
Input Length (bits): NC × (N–K+S–P) × M Erasures Length (symbols): NC × (N–K+S–P) Output Length (bits): NC × S × M |
N is the codeword length.
K is the message word length.
S is the shortened message word length.
NC is the number of codewords (and message words).
P is the number of punctures per codeword, and is equal to the number of zeros in the puncture vector.
M is the degree of the primitive polynomial. Each group of M bits represents an integer between
0and2M–1that belongs to the finite Galois fieldGF(2M).
For more information on representing data for Reed-Solomon codes, see Integer Format (Reed-Solomon Only).
Restrictions on the M and the Codeword Length N
If you do not select Specify primitive polynomial, valid values for the codeword length, N, are from 7 to 65535. In this case, the block uses the default primitive polynomial of degree
M = ceil(log2(N+1)). You can display the default primitive polynomial by runningprimpoly(ceil(log2(N+1))).If you select Specify primitive polynomial, valid values for the primitive polynomial degree, M, are from 3 to 16. The valid values for N in this case are from 7 to 2M–1. Selecting Specify primitive polynomial enables you to specify the primitive polynomial that defines the finite field GF(2M), which corresponds to the values that form message words and codewords.
Specify the Generator Polynomial
Select Specify generator polynomial to enable the Generator polynomial parameter for specifying the generator polynomial of the Reed-Solomon code. Enter an integer row vector with element values from 0 to 2M-1. The vector represents a polynomial, in descending order of powers, whose coefficients are elements of GF(2M) represented in integer format. For more information about integer and binary format, see Integer Format (Reed-Solomon Only). The generator polynomial must be equal to a polynomial with this factored form:
g(x) = (x+αb)(x+αb+1)(x+αb+2)...(x+αb+N-K-1)
α is the primitive element of the Galois field over which the input message is defined, and b is an integer.
If you do not select Specify generator polynomial, the block uses the
default generator polynomial, corresponding to b=1, for Reed-Solomon
encoding. You can display the default generator polynomial by running rsgenpoly.
If you are using the default primitive polynomial (Specify primitive polynomial is not selected), the default generator polynomial is
rsgenpoly(N,K), whereN = 2M-1.If you are not using the default primitive polynomial (Specify primitive polynomial is selected) and you specify the primitive polynomial as
poly, the generator polynomial isrsgenpoly(N,K,poly).
Note
The degree of the generator polynomial is N − K, where N is the codeword length and K is the message word length.
Puncturing and Erasures
1s and 0s have
precisely opposite meanings for the puncture and erasure vectors.
In a puncture vector,
1means that the data symbol is passed through the block unaltered.0means that the data symbol is to be punctured, or removed, from the data stream.
In an erasure vector,
1means that the data symbol is to be replaced with an erasure symbol.0means that the data symbol is passed through the block unaltered.
These conventions apply to both the encoder and the decoder. For more information, see Shortening, Puncturing, and Erasures.
Supported Data Types
| Port | Supported Data Types |
|---|---|
| In |
|
| Out |
Algorithms
This object implements the algorithm, inputs, and outputs described in Algorithms for BCH and RS Errors-only Decoding.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
Version History
Introduced before R2006a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)