comm.Descrambler
Descramble input signal
Description
The comm.Descrambler
System object™ applies multiplicative descrambling to input data. It performs the inverse
operation of the comm.Scrambler object used in the transmitter.
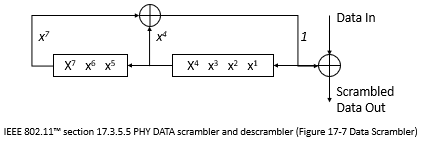
This schematic shows the multiplicative descrambler operation. The adders and subtracter operate modulo N, where N is the value specified by the CalculationBase property.

At each time step, the input causes the contents of the registers to shift sequentially.
Using the Polynomial property, you specify the on
or off state for each switch in the descrambler. To make the comm.Descrambler
object reverse the operation of the comm.Scrambler object, use the same property
settings in both objects. If there is no signal delay between the scrambler and the descrambler,
then the InitialConditions in the two
objects must be the same.
Note
To apply additive descrambling to input data, you can use the comm.PNSequence
System object and the xor function. For an example, see Additive Scrambling of Input Data.
To descramble an input signal:
Create the
comm.Descramblerobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Creation
Syntax
Description
descrambler = comm.Descrambler
descrambler = comm.Descrambler(base,poly,cond)base, the Polynomial property set to
poly, and the InitialConditions property set
to cond.
Example: comm.Descrambler(8,'1 + x^-2 + x^-3 + x^-5 + x^-7',[0 3 2 2 5 1
7]) sets the calculation base to 8, and the descrambler
polynomial and initial conditions as specified.
descrambler = comm.Descrambler(___,Name,Value)
Example: comm.Descrambler('CalculationBase',2)
Properties
Usage
Syntax
Description
descrambledOut = descrambler(signal)
descrambledOut = descrambler(signal,initcond)
This syntax applies when you set the InitialConditionsSource
property of the object to 'Input port'.
descrambledOut = descrambler(signal,reset)
This syntax applies when you set the InitialConditionsSource
property of the object to 'Property' and the ResetInputPort to
true.
Input Arguments
Output Arguments
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
Examples
Extended Capabilities
Version History
Introduced in R2012a