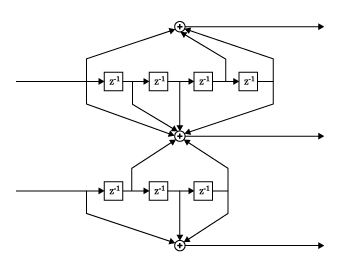
distspec
Compute distance spectrum of convolutional code
Description
spect = distspec(trellis,numcomp)
Examples
Input Arguments
Output Arguments
Algorithms
The function uses a tree search algorithm implemented with a stack, as described in [2].
References
[1] Bocharova, I.E., and B.D. Kudryashov. “Rational Rate Punctured Convolutional Codes for Soft-Decision Viterbi Decoding.” IEEE Transactions on Information Theory 43, no. 4 (July 1997): 1305–13. https://doi.org/10.1109/18.605600.
[2] Cedervall, M.L., and R. Johannesson. “A Fast Algorithm for Computing Distance Spectrum of Convolutional Codes.” IEEE Transactions on Information Theory 35, no. 6 (November 1989): 1146–59. https://doi.org/10.1109/18.45271.
[3] Chang J., D. Hwang, and M. Lin. “Some Extended Results on the Search for Good Convolutional Codes.” IEEE Transactions on Information Theory 43, no. 5 (September 1997): 1682–97. https://doi.org/10.1109/18.623175.
[4] Frenger, P.K., P. Orten, and T. Ottosson. “Comments and Additions to Recent Papers on New Convolutional Codes.” IEEE Transactions on Information Theory 47, no. 3 (March 2001): 1199–1201. https://doi.org/10.1109/18.915683.
Version History
Introduced before R2006a