M-PSK TCM Encoder
Convolutionally encode binary data and modulate using PSK method
Library
TCM, in Digital Baseband sublibrary of Modulation
Description
The M-PSK TCM Encoder block implements trellis-coded modulation (TCM) by convolutionally encoding the binary input signal and mapping the result to a PSK signal constellation.
The M-ary number parameter is the number of points in the signal constellation, which also equals the number of possible output symbols from the convolutional encoder. (That is, log2(M-ary number) is equal to n for a rate k/n convolutional code.)
Input Signals and Output Signals
If the convolutional encoder described by the trellis structure represents a rate k/n code, then the block input signal must be a binary column vector with a length of L*k for some positive integer L.
This block accepts a binary-valued input signal. The output signal is a complex column vector of length L.
Specifying the Encoder
To define the convolutional encoder, use the Trellis structure parameter. This parameter is a MATLAB® structure whose format is described in Trellis Description of a Convolutional Code. You can use this parameter field in two ways:
If you want to specify the encoder using its constraint length, generator polynomials, and possibly feedback connection polynomials, then use a
poly2trelliscommand within the Trellis structure field. For example, to use an encoder with a constraint length of 7, code generator polynomials of 171 and 133 (in octal numbers), and a feedback connection of 171 (in octal), set the Trellis structure parameter topoly2trellis(7,[171 133],171)If you have a variable in the MATLAB workspace that contains the trellis structure, then enter its name as the Trellis structure parameter. This way is faster because it causes Simulink® software to spend less time updating the diagram at the beginning of each simulation, compared to the usage in the previous bulleted item.
The encoder registers begin in the all-zeros state. You can configure the encoder
so that it resets its registers to the all-zeros state during the course of the
simulation. To do this, set the Operation mode to Reset
on nonzero input via port. The block then opens a second input port,
labeled Rst. The signal at the Rst port is a
scalar signal. When it is nonzero, the encoder resets before processing the data at
the first input port.
Signal Constellations
The trellis-coded modulation technique partitions the constellation into subsets called cosets, so as to maximize the minimum distance between pairs of points in each coset. This block internally forms a valid partition based on the value you choose for the M-ary number parameter.
The figure below shows the labeled set-partitioned signal constellation that the block uses when M-ary number is 8. For constellations of other sizes, see [1].
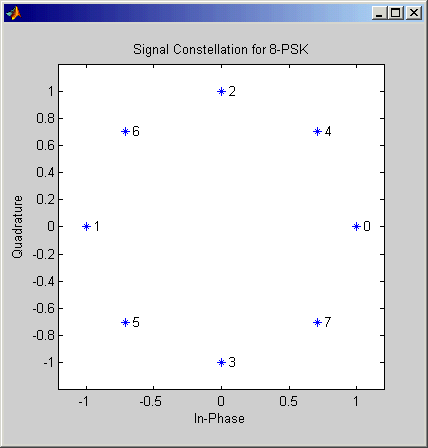
Coding Gains
Coding gains of 3 to 6 decibels, relative to the uncoded case can be achieved in the presence of AWGN with multiphase trellis codes [3].
Parameters
- Trellis structure
MATLAB structure that contains the trellis description of the convolutional encoder.
- Operation mode
In
Continuousmode (default setting), the block retains the encoder states at the end of each frame, for use with the next frame.In
Truncated (reset every frame)mode, the block treats each frame independently. I.e., the encoder states are reset to all-zeros state at the start of each frame.In
Terminate trellis by appending bitsmode, the block treats each frame independently. For each input frame, extra bits are used to set the encoder states to all-zeros state at the end of the frame. The output length is given by , where x is the number of input bits, and (or, in the case of multiple constraint lengths, s =sum(ConstraintLength(i)-1)). The block supports this mode for column vector input signals.In
Reset on nonzero input via portmode, the block has an additional input port, labeledRst. When theRstinput is nonzero, the encoder resets to the all-zeros state.- M-ary number
The number of points in the signal constellation.
- Output data type
The output type of the block can be specified as a
singleordouble. By default, the block sets this todouble.
Pair Block
References
[1] Biglieri, E., D. Divsalar, P. J. McLane and M. K. Simon, Introduction to Trellis-Coded Modulation with Applications, New York, Macmillan, 1991.
[2] Proakis, John G., Digital Communications, Fourth edition, New York, McGraw-Hill, 2001
[3] Ungerboeck, G., “Channel Coding with Multilevel/Phase Signals”, IEEE Trans. on Information Theory, Vol IT28, Jan. 1982, pp. 55–67.
Extended Capabilities
Version History
Introduced before R2006a
