Rectangular QAM Demodulator Baseband
Demodulate rectangular-QAM-modulated data
Libraries:
Communications Toolbox /
Modulation /
Digital Baseband Modulation /
AM
Communications Toolbox HDL Support /
Modulation /
AM
Description
The Rectangular QAM Demodulator Baseband block demodulates a signal that was modulated using M-ary quadrature amplitude modulation with a constellation on a rectangular lattice.
Note
All values of power assume a nominal impedance of 1 ohm.
Examples
Demodulate Noisy QAM Signal
Modulate and demodulate a noisy QAM signal.
Use the Open model button to open the QAM demodulation model.

Run the simulation. The results are saved to the base workspace, where the variable ErrorVec is a 1-by-3 row vector. The BER is found in the first element.
Display the error statistics. For the Eb/No provided, 2 dB, the resultant BER is approximately 0.1. Your results may vary slightly.
ans =
0.0947
Increase the Eb/No to 4 dB. Rerun the simulation, and observe that the BER has decreased.
ans =
0.0139
Ports
Input
In — QAM-modulated signal
scalar | vector
QAM-modulated signal, specified as a scalar or column vector. This
port is unnamed until the Var port is
enabled.
Data Types: double | single | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | Boolean | fixed point
Complex Number Support: Yes
Var — Noise Variance
positive scalar | vector of positive values
Noise variance, specified as a positive scalar or vector of positive values. When the noise variance or signal power result in computations involving extreme positive or negative magnitudes, see Soft Demodulation for demodulation decision type considerations.
Dependencies
To enable this parameter, set the Noise variance source
parameter to Port.
Data Types: double
Output
Out — Demodulated signal
scalar | vector
Demodulated signal, returned as a scalar, or vector. The dimensions of the demodulated signal depend on the specified Output type and Decision type. This port is unnamed on the block.
Parameters
To edit block parameters interactively, use the Property Inspector. From the Simulink® Toolstrip, on the Simulation tab, in the Prepare gallery, select Property Inspector.
Main
M-ary number — Modulation order
16 (default) | positive integer
Modulation order, specified as a positive integer power of two. The modulation order, M, specifies the number of points in the signal constellation. M must have the form 2K for some positive integer K. The block scales the signal constellation based on how you set the Normalization method parameter. For more information, see Constellation Size and Scaling.
Output type — Output type
Integer (default) | Bit
Determines whether the block produces integers or binary representations of integers.
When you set Output type to
Integer, the block produces integers in the range [0, (M – 1)] for each symbol. M is M-ary number.When you set Output type to
Bitand Decision type toHard decision, the block produces a group of K bits, called a binary word, for each symbol. K=log2(M).When you set Output type to
Bitand Decision type toLog-likelihood ratioorApproximate log-likelihood ratio, the block outputs bitwise LLR or approximate LLR, respectively.
Decision type — Demodulation decision type
Hard decision (default) | Log-likelihood ratio | Approximate log-likelihood ratio
Demodulation decision type, specified as Hard decision,
Log-likelihood ratio, or
Approximate log-likelihood ratio. For
algorithm selection considerations, see Hard- vs. Soft-Decision Demodulation.
Dependencies
This parameter appears when you set Output type to
Bit.
Noise variance source — Noise variance source
Dialog (default) | Port
Noise variance source, specified as Dialog
or Port.
When you select
Dialog, you must use theNoise varianceparameter to set the noise variance.When you select
Port, you must use theVarport to set the noise variance.
Dependencies
This parameter appears when you set Decision type to
Approximate log-likelihood ratio or
Log-likelihood ratio.
Noise variance — Noise Variance
1 (default) | positive scalar | vector of positive values
Noise variance, specified as a positive scalar or vector of positive values.
When you specify this parameters as a scalar, that value is used on all elements in the input signal.
When you specify this parameters as a vector, the vector length must be equal to the number of columns in the input signal. Each noise variance vector element is applied to its corresponding column in the input signal.
This parameter is tunable in normal mode, Accelerator mode and Rapid Accelerator mode.
If you use the Simulink Coder™ rapid simulation (RSIM) target to build an RSIM executable, then you can tune the parameter without recompiling the model. This is useful for Monte Carlo simulations in which you run the simulation multiple times (perhaps on multiple computers) with different amounts of noise.
The exact LLR algorithm computes exponentials using finite precision arithmetic. For computations involving very large positive or negative magnitudes, the exact LLR algorithm yields:
Infor-Infif the noise variance is a very large valueNaNif the noise variance and signal power are both very small values
The approximate LLR algorithm does not compute exponentials. You can avoid
Inf, -Inf, and NaN results by using
the approximate LLR algorithm.
Dependencies
To enable this parameter, set the Decision type parameter to either
Log-likelihood ratio or
Approximate log-likelihood ratio and
set the Noise variance source parameter to
Dialog.
Constellation ordering — Mapping order of symbols
Binary (default) | Gray | User-defined
Mapping order of the symbols, specified as Gray,
Binary, or
User-defined. This parameter determines
how the block maps each symbol to a group of output bits or
integer.
Constellation mapping — User-defined constellation mapping
[0:15] (default) | vector
Constellation mapping that you define, specified as an M-element containing unique integer values in the range [0, (M – 1)].
The first element of this vector corresponds to the top-leftmost point of the constellation, with subsequent elements running down column-wise, from left to right. The last element corresponds to the bottom-rightmost point.
Dependencies
This parameter appears when you set Constellation ordering to
User-defined.
Normalization method — Scaling method for constellation
Min. distance between
symbols (default) | Average Power | Peak Power
Scaling method for the constellation, specified as Min. distance between
symbols, Average Power, or
Peak Power. For more information, see
Constellation Size and Scaling
Minimum distance — Distance between two nearest constellation points
2 (default) | positive scalar
Distance between the two nearest constellation points, specified as a positive scalar.
Dependencies
This parameter appears when you set Normalization method to Min. distance
between symbols.
Average power, referenced to 1 ohm (watts) — Average power
1 (default) | positive scalar
Average power of the symbols in the constellation in watts, specified as a positive scalar. Power values assume a nominal impedance of 1 ohm.
Dependencies
This parameter appears when you set Normalization method to Average
Power.
Peak power, referenced to 1 ohm (watts) — Maximum power
1 (default) | positive scalar
Maximum power of the symbols in the constellation in watts, specified as a positive scalar. Power values assume a nominal impedance of 1 ohm.
Dependencies
This parameter appears when you set Normalization method to Peak
Power.
Phase offset (rad) — Rotation of signal constellation
0 (default) | numeric scalar
Rotation of the signal constellation in radians, specified as a numeric scalar.
Data Types
Output data type — Output data type
Inherit via internal
rule (default) | Smallest unsigned integer | double | single | int8 | uint8 | int16 | uint16 | int32 | uint32 | boolean
Output data type, specified as Inherit via internal rule,
Smallest unsigned integer,
double,
single, int8,
uint8, int16,
uint16, int32,
uint32, or
boolean.
When you select
Inherit via internal rule, the block inherits the data type based on an internal rule. For more information on this rule, see Inherit via Internal Rule. The output data type will be the same as the input data type if the input is of typesingleordouble. Otherwise, the output data type will be as if this parameter is set to'Smallest unsigned integer'.When the parameter is set to
'Smallest unsigned integer', the block sets the output data type based on the settings used in the Hardware Implementation pane of the Configuration Parameters dialog box of the model. IfASIC/FPGAis selected in the Hardware Implementation pane, the output data type is the ideal minimum size, i.e.,ufix(1)for bit outputs, andufix(ceil(log2(M)))for integer outputs. For all other selections, it is an unsigned integer with the smallest available word length large enough to fit the ideal minimum size, usually corresponding to the size of a char (e.g.,uint8).For integer outputs, this parameter can be set to
Smallest unsigned integer,int8,uint8,int16,uint16,int32,uint32,single, anddouble. For bit outputs, the options areSmallest unsigned integer,int8,uint8,int16,uint16,int32,uint32,boolean,single, ordouble.
Derotate factor — Derotate factor data type
Inherit: Same word length as
input (default) | fixdt(1,16) | <data type expression>
Specify the derotate factor data type as Inherit: Same word length as
input, fixdt(1,16), or
<data type expression>.
For information about specifying data types, see Data Type Assistant.
Dependencies
This parameter applies only when the input is fixed-point and Phase offset (rad) is not a multiple of π/2.
Denormalization factor — Denormalization factor data type
Inherit: Same word length as
input (default) | fixdt(1,16) | <data type expression>
Specify the denormalization factor data type as Inherit:
Same word length as input,
fixdt(1,16), or <data
type expression>. This scaling factor is derived from
Normalization method and other parameter
values in the block dialog. A best-precision fraction length is always
used.
For information about specifying data types, see Data Type Assistant.
Dependencies
This parameter applies only when the input is fixed-point and the derived denormalization factor is nonunity (not equal to 1).
Product output — Product output data type
Inherit: Inherit via internal
rule (default) | fixdt(1,16) | <data type expression>
Specify the product data type as Inherit: Inherit via internal
rule, fixdt(1,16), or
<data type expression>.
When you select Inherit: Inherit via internal rule, the block
computes the full-precision product word length and fraction length. For
information about the full-precision Product
output internal rule, see Internal Rule for
Product Data Types.
The block uses rounding mode when the result of a fixed-point calculation does not map exactly to a number representable by the data type and scaling storing the result. For more information, see Rounding Modes or Rounding Mode: Simplest (Fixed-Point Designer).
For information about specifying data types, see Data Type Assistant.
Dependencies
This parameter only applies when the input is a fixed-point signal and there is a nonunity (not equal to 1) denormalized factor.
Rounding mode — Rounding mode for fixed-point operations
Wrap (default) | Saturate
Specify the rounding mode for Product output fixed-point operations as
Wrap or
Saturate. The block uses rounding mode
when the result of a fixed-point calculation does not map exactly to a
number representable by the data type. For more information, see Rounding
Modes or Rounding Mode: Simplest (Fixed-Point Designer).
Dependencies
This parameter applies for Product output only.
Saturate on integer overflow — Option to saturate on integer overflow
off (default) | on
Select this check box to saturate on integer overflow.
Dependencies
This parameter applies for Product output only.
Sum — Sum data type
Inherit: Inherit via internal
rule (default) | Inherit: Same as product output | fixdt(1,16) | <data type expression>
Specify the sum data type as Inherit: Inherit via internal
rule, Inherit: Same as product
output, fixdt(1,16), or
<data type expression>.
When you select
Inherit: Inherit via internal rule, the block computes the full-precision sum word length and fraction length, based on the two inputs to the Sum in the fixed-point Hard Decision Algorithm signal flow diagram. The rule is the same as the fixed-point inherit rule of the internal Accumulator data type parameter in the Sum (Simulink) block.When you select
Inherit: Same as product outputand Product output is used, the block configures the data type of the Sum parameter to be the same as the Product output data type. If the Product output is not used, then this setting will be ignored, and theInherit: Inherit via internal ruleand the Sum parameter setting is used.
For information about specifying data types, see Data Type Assistant.
Dependencies
This parameter applies only when the input is a fixed-point signal.
Block Characteristics
More About
Data Type Assistant
The Data Type Assistant helps you set data
attributes. To use the Data Type Assistant, click Show data type
assistant
![]() . For more information, see Specify Data Types Using Data Type Assistant (Simulink).
. For more information, see Specify Data Types Using Data Type Assistant (Simulink).
Algorithms
For algorithm considerations, see Hard- vs. Soft-Decision Demodulation.
QAM Hard-Decision Demodulation
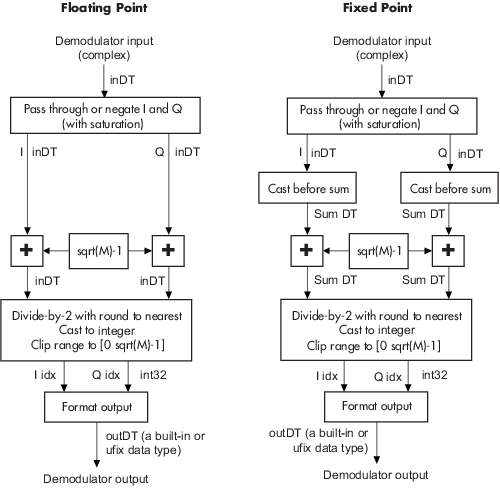
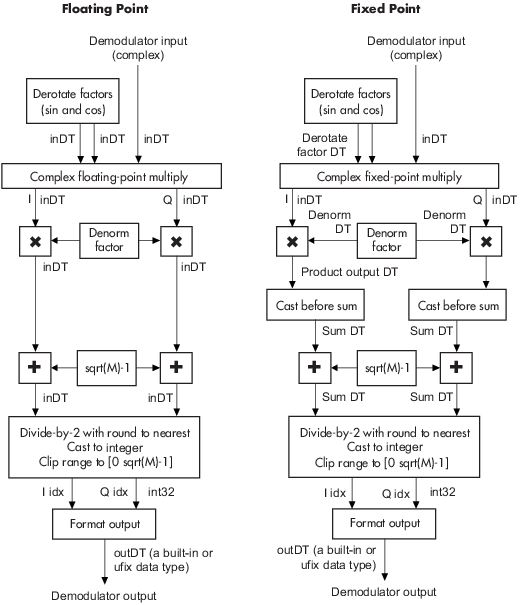
The demodulator algorithm maps received input signal constellation values to M-ary integer I and Q symbol indices in the range [0, ] and then maps these demodulated symbol indices to formatted output values. M is the M-ary number parameter value.
The integer symbol index computation is performed by first derotating and scaling the complex input signal constellation (possibly with noise) by a derotate factor and denormalization factor, respectively. These factors are derived from the Phase offset (rad), Normalization method, and related parameters. These derotated and denormalized values are added to to translate them into an approximate range of [0, (2×()+N)]. N is the added noise value. The resulting values are then rescaled via a divide-by-two (or, equivalently, a right-shift by one bit for fixed-point operation) to obtain a range of approximately [0, ( + N)] for I and Q. The noisy index values are rounded to the nearest integer and clipped, via saturation, and then mapped to integer symbol values in the range [0, M – 1]. Finally, based on other block parameters, the integer index is mapped to a symbol value that gets formatted and cast to the selected Output data type.
These figures signal flow diagrams for floating-point and fixed-point algorithm operation.
The floating-point diagrams apply when the input signal data type is
double or single. The fixed-point diagrams
apply when the input signal is a signed fixed-point data type. The diagram is
simplified when Phase offset (rad) is a multiple of π/2 or
the derived denormalization factor is 1.
Signal-Flow Diagrams with Trivial Phase Offset and Denormalization Factor Equal to 1
Signal-Flow Diagrams with Nontrivial Phase Offset and Nonunity Denormalization Factor
Soft Demodulation
For soft demodulation, two soft-decision log-likelihood ratio (LLR) algorithms are available: exact LLR and approximate LLR. The exact LLR algorithm is more accurate but has slower execution speed than the approximate LLR algorithm. For further description of these algorithms, see the Hard- vs. Soft-Decision Demodulation topic.
Note
The exact LLR algorithm computes exponentials using finite precision arithmetic. For computations involving very large positive or negative magnitudes, the exact LLR algorithm yields:
Infor-Infif the noise variance is a very large valueNaNif the noise variance and signal power are both very small values
The approximate LLR algorithm does not compute exponentials. You can avoid
Inf, -Inf, and NaN results by using
the approximate LLR algorithm.
Constellation Size and Scaling
The signal constellation has M points, where M is the M-ary number parameter. M must have the form 2K for some positive integer K. The block scales the signal constellation based on how you set the Normalization method parameter. The following table lists the possible scaling conditions.
| Value of Normalization Method Parameter | Scaling Condition |
|---|---|
Min. distance between symbols
| The nearest pair of points in the constellation is separated by the value of the Minimum distance parameter. |
Average Power
| The average power of the symbols in the constellation is the Average power, referenced to 1 ohm (watts) parameter. |
Peak Power
| The maximum power of the symbols in the constellation is the Peak power, referenced to 1 ohm (watts) parameter. |
References
[1] Smith, J. G., "Odd-Bit Quadrature Amplitude-Shift Keying," IEEE Transactions on Communications, Vol. COM-23, March 1975, pp. 385–389.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
HDL Code Generation
Generate VHDL, Verilog and SystemVerilog code for FPGA and ASIC designs using HDL Coder™.
HDL Coder™ provides additional configuration options that affect HDL implementation and synthesized logic.
This block has one default HDL architecture.
| ConstrainedOutputPipeline | Number of registers to place at
the outputs by moving existing delays within your design. Distributed
pipelining does not redistribute these registers. The default is
|
| InputPipeline | Number of input pipeline stages
to insert in the generated code. Distributed pipelining and constrained
output pipelining can move these registers. The default is
|
| OutputPipeline | Number of output pipeline stages
to insert in the generated code. Distributed pipelining and constrained
output pipelining can move these registers. The default is
|
The block does not support
singleordoubledata types for HDL code generation.HDL Coder supports the following Output type options:
IntegerBitis supported only if the Decision Type isHard decision.
You must set Normalization Method to
Minimum Distance Between Symbols, with a Minimum distance of 2.You must set Phase offset (rad) to a value that is a multiple of
pi/4.
Version History
Introduced before R2006a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)