Apply OFDM in MIMO Simulation
Use an OFDM modulator and demodulator in a simple, 2x2 single-user MIMO error rate simulation. The OFDM parameters are based on the 802.11n standard.
Create an OFDM modulator and demodulator pair with user-specified pilot indices, an inserted DC null, two transmit antennas, and two receive antennas. Specify pilot indices that vary across antennas.
ofdmMod = comm.OFDMModulator(FFTLength=128, ... PilotInputPort=true, ... NumSymbols=3, ... PilotCarrierIndices= ... cat(3,[12; 40; 54; 76; 90; 118],[13; 39; 55; 75; 91; 117]), ... InsertDCNull=true, ... NumTransmitAntennas=2); ofdmDemod = comm.OFDMDemodulator(ofdmMod); ofdmDemod.NumReceiveAntennas = 2;
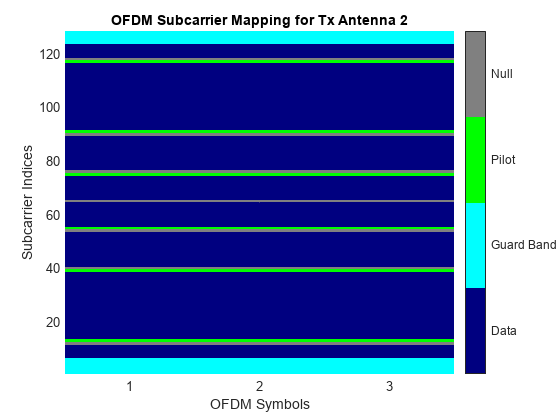
Show the resource mapping of pilot subcarriers for each transmit antenna. The gray lines in the figure denote the insertion of null subcarriers to minimize pilot signal interference.
showResourceMapping(ofdmMod)

Determine the dimensions of the OFDM modulator by using the info method.
ofdmModDim = info(ofdmMod); numDataSc = ofdmModDim.DataInputSize(1); % Number of data subcarriers numSym = ofdmModDim.DataInputSize(2); % Number of OFDM symbols numTxAnt = ofdmModDim.DataInputSize(3); % Number of transmit antennas
Set parameters to generate 100 OFDM frames using QPSK modulation.
nframes = 100;
M = 4; % Modulation order to QPSKCreate an error rate counter.
errorRate = comm.ErrorRate;
Simulate the OFDM system over 100 frames assuming a flat, 2x2, Rayleigh fading channel. Remove the effects of multipath fading using a simple, least squares solution, and demodulate the OFDM waveform and QPSK data. Generate error statistics by comparing the original data with the demodulated data.
for k = 1:nframes % Generate a frame of user data dataIn = randi([0 M-1],numDataSc*numSym*numTxAnt,1); % Split the user data into two different streams and map to QPSK % symbols streamDataOut = reshape(dataIn,numTxAnt,[]).'; mapperOut = pskmod(streamDataOut,M,pi/4); % Generate random OFDM pilot symbols pilotData = complex(rand(ofdmModDim.PilotInputSize), ... rand(ofdmModDim.PilotInputSize)); % Reshape the modulated data streams to match the OFDM modulator % requirements and modulate the symbols using OFDM ofdmModData = reshape(mapperOut,numDataSc,numSym,numTxAnt); dataOFDM = ofdmMod(ofdmModData,pilotData); % Create flat, i.i.d., Rayleigh fading channel 2-by-2 channel chGain = complex(randn(2,2),randn(2,2))/sqrt(2); % Pass OFDM signal through Rayleigh and AWGN channels receivedSignal = awgn(dataOFDM*chGain,30); % Apply least squares solution to remove effects of fading channel rxSigMF = chGain.' \ receivedSignal.'; % Demodulate OFDM data receivedOFDMData = ofdmDemod(rxSigMF.'); % Form the received streams receivedOFDMStreams = reshape(receivedOFDMData,[],numTxAnt); % Demodulate QPSK data receivedStreams = pskdemod(receivedOFDMStreams,M,pi/4); % Demap the data from each rx stream back to the user data receivedData = reshape(receivedStreams.',[],1); % Compute error statistics errors = errorRate(dataIn,receivedData); end
Display the error statistics.
fprintf('\nSymbol error rate = %d from %d errors in %d symbols\n',errors)Symbol error rate = 8.996795e-02 from 5614 errors in 62400 symbols
