Reed-Solomon Coding with Erasures, Punctures, and Shortening in Simulink
This model shows how to configure Reed-Solomon (RS) codes to perform block coding with erasures, punctures, and shortening.
RS decoders can correct both errors and erasures. The erasures can be generated by a receiver that identifies the most unreliable symbols in a given codeword. When a receiver erases a symbol, it replaces the symbol with a zero and passes a flag to the decoder indicating that the symbol is an erasure, not a valid code symbol.
In addition, an encoder can generate punctures for which specific parity symbols are always removed from its output. The decoder, which knows the puncture pattern, inserts zeros in the puncture positions and treats those symbols as erasures. The decoder treats encoder-generated punctures and receiver-generated erasures in exactly the same way when it decodes.
Puncturing has the added benefit of making the code rate a bit more flexible, at the expense of some error correction capability. Shortened codes achieve the same code rate flexibility without degrading the error correction performance, given the same demodulator input Eb/N0. Note that puncturing is the removal of parity symbols from a codeword, and shortening is the removal of message symbols from a codeword.
Decoding with Receiver Generated Erasures
This example shows a (63,53) RS code operating in concert with a 64-QAM modulation scheme. Since the code can correct (63-53)/2 = 5 errors, it can alternatively correct (63-53) = 10 erasures. For each demodulated codeword, the receiver determines the six least reliable symbols by finding the symbols within a decision region that are nearest to a decision boundary. It then erases those symbols. The RSCodingErasuresExample model is shown here.
model_e = 'RSCodingErasuresExample';
open_system(model_e);



Simulation and Visualization with Erasures Only
Define system simulation parameters:
RS_TsUncoded = 1; % Sample time (s) RS_n = 63; % Codeword length RS_k = 53; % Message length RS_MQAM = 64; % QAM order RS_numBitsPerSymbol = ... % 6 bits per symbol log2(RS_MQAM); RS_sigPower = 42; % Assume points at +/-1, +/-3, +/-5, +/-7 RS_numErasures = 6; % Number of erasures RS_EbNoUncoded = 15; % In dB
The system is simulated at an uncoded Eb/N0 of 15 dB. However, the coded Eb/N0 is reduced because of the redundant symbols added by the RS Encoder. Also, the period of each frame in the model remains constant at 53 seconds, corresponding to a sample time of 1 second at the output of the Random Integer Generator. Moreover, the symbol time at the output of the RS Encoder is reduced by a factor of the code rate, because 63 symbols are output over the frame time of 53 seconds. The AWGN Channel block accounts for this by using these parameters:
RS_EbNoCoded = RS_EbNoUncoded + 10*log10(RS_k/RS_n); RS_TsymCoded = RS_TsUncoded * (RS_k/RS_n);
The receiver determines which symbols to erase by finding the 64-QAM symbols, per codeword, that are closest to a decision boundary. It deletes the six least reliable code symbols, which still allows the RS Decoder to correct (10-6)/2 = 2 errors per codeword.
Run the simulation and show the received symbols and those symbols that were erased.
sim(model_e) open_system([model_e,'/Received Signal Scatter Plot']) open_system([model_e,'/Erased Signal Scatter Plot']) %


BER Performance with Erasures Only
Examine the BER performance at the output of the decoder. We set the stop time of the simulation to inf, then simulate until 100 bit errors are collected out of the RS Decoder. Display the total number of corrected errors, 64-QAM BER, and RS BER.
fprintf('Total number of corrected errors with\n') fprintf('erasures: %d\n',totCorrErrors_e(1)) fprintf('64-QAM BER with\n') fprintf('erasures: %s\n',channelBER_e(1)) fprintf('RS BER with\n') fprintf('erasures: %s\n',codedBER_e(1))
Total number of corrected errors with erasures: 9595 64-QAM BER with erasures: 1.702468e-03 RS BER with erasures: 1.851795e-06
Simulation with Erasures and Punctures
In addition to decoding receiver-generated erasures, the RS Decoder can correct encoder-generated punctures. The decoding algorithm is identical for the two cases, but the per-codeword sum of the punctures and erasures cannot exceed twice the error-correcting capability of the code. Consider the following model that performs decoding for both erasures and punctures.
The same puncture vector is specified in both the encoder and decoder blocks. This example punctures two symbols from each codeword. Vector values of "1" indicate nonpunctured symbols, while values of "0" indicate punctured symbols. In the erasures vector, however, values of "1" indicate erased symbols, while values of "0" indicate nonerased symbols.
Several of the parameters for the AWGN Channel block are now slightly different, because the length of the codeword is now different from the previous example. The block accounts for the size difference with the following code:
RS_numPuncs = 2; RS_EbNoCoded = RS_EbNoUncoded + 10*log10(RS_k / (RS_n - RS_numPuncs)); RS_TsymCoded = RS_TsUncoded * (RS_k / (RS_n - RS_numPuncs));
We simulate the model, RSCodingErasuresPunctExample.mdl, collecting 1000 errors out of the RS Decoder block. Due to puncturing, the signal dimensions out of the encoder are 61-by-1, rather than 63-by-1 in the model with no puncturing. The Create Erasures Vector subsystem must also account for the size differences as it creates a 61-by-1 erasures vector. The RSCodingErasuresPunctExample model is shown here.
model_ep = 'RSCodingErasuresPunctExample';
open_system(model_ep);

sim(model_ep)
BER Performance with Erasures and Punctures
Compare the BERs for erasures decoding with and without puncturing.
The BER out of the 64-QAM Demodulator is slightly better in the punctured case, because the Eb/N0 into the demodulator is slightly higher. However, the BER out of the RS Decoder is much worse in the punctured case, because the two punctures reduce the error correcting capability of the code by one, leaving it able to correct only (10-6-2)/2 = 1 error per codeword. Display the total number of corrected errors, 64-QAM BER, and RS BER for the RS codes with erasures and punctures.
fprintf('Total number of corrected errors with\n') fprintf(' erasures: %d\n',totCorrErrors_e(1)) fprintf('erasures and punctures: %d\n',totCorrErrors_ep(1)) fprintf('64-QAM BER with\n') fprintf(' erasures: %s\n',channelBER_e(1)) fprintf('erasures and punctures: %s\n',channelBER_ep(1)) fprintf('RS BER with\n') fprintf(' erasures: %s\n',codedBER_e(1)) fprintf('erasures and punctures: %s\n',codedBER_ep(1))
Total number of corrected errors with
erasures: 9595
erasures and punctures: 2578
64-QAM BER with
erasures: 1.702468e-03
erasures and punctures: 1.471001e-03
RS BER with
erasures: 1.851795e-06
erasures and punctures: 4.289038e-05
Specifying a Shortened Code
Shortening a block code removes symbols from its message portion, where puncturing removes symbols from its parity portion. You can incorporate both techniques with the RS encoder and decoder blocks.
For example, to shorten a (63,53) code to a (53,43) code, you can simply enter 63, 53 and 43 for n, k, and s respectively, in the encoder and decoder block masks. The RSCodingErasuresPunctShortExample model is shown here.
model_eps = 'RSCodingErasuresPunctShortExample';
open_system(model_eps);
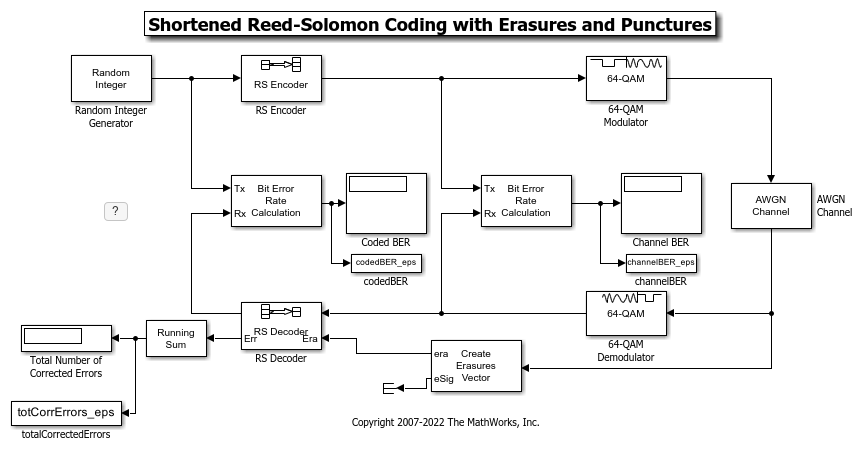
Simulation with Erasures, Punctures, and Shortening
Because shortening alters the code rate much like puncturing does, the AWGN parameters must be changed again. The AWGN Channel block accounts for this with the following code:
RS_EbNoCoded = RS_EbNoUncoded + ...
10*log10(RS_s / (RS_n - RS_k + RS_s - RS_numPuncs));
RS_TsymCoded = RS_TsUncoded * RS_s / (RS_n - RS_k + RS_s - RS_numPuncs);
We simulate the model, once again collecting 1000 errors out of the RS Decoder block. Note that the signal dimensions out of the RS Encoder are 26x1, due to 35 symbols of shortening and 2 symbols of puncturing. Once again, the Create Erasures Vector subsystem must also account for the size difference caused by the shortened code.
sim(model_eps)
BER Performance with Erasures, Punctures, and Shortening
Compare the BER performance for decoding with erasures only, with erasures and punctures, and with erasures, punctures, and shortening.
The BER out of the 64-QAM Demodulator is worse with shortening than it is without shortening. This is because the code rate of the shortened code is much lower than the code rate of the non-shortened code and therefore the coded Eb/N0 into the demodulator is worse with shortening. A shortened code has the same error correcting capability as non-shortened code for the same Eb/N0, but the reduction in Eb/N0 manifests in the form of a higher BER out of the RS Decoder with shortening than without. Compare the total number of corrected errors, 64-QAM BER, and RS BER for the RS codes with erasures, punctures, and shortening.
fprintf('Total number of corrected errors\n') fprintf( ... ' erasures: %d\n',totCorrErrors_e(1)) fprintf( ... ' erasures and punctures: %d\n',totCorrErrors_ep(1)) fprintf( ... 'erasures, punctures, and shortening: %d\n',totCorrErrors_eps(1)) fprintf('64-QAM BER with\n') fprintf(' erasures: %s\n',channelBER_e(1)) fprintf(' erasures and punctures: %s\n',channelBER_ep(1)) fprintf('erasures, punctures, and shortening: %s\n',channelBER_eps(1)) fprintf('RS BER with\n') fprintf(' erasures: %s\n',codedBER_e(1)) fprintf(' erasures and punctures: %s\n',codedBER_ep(1)) fprintf('erasures, punctures, and shortening: %s\n',codedBER_eps(1))
Total number of corrected errors
erasures: 9595
erasures and punctures: 2578
erasures, punctures, and shortening: 3120
64-QAM BER with
erasures: 1.702468e-03
erasures and punctures: 1.471001e-03
erasures, punctures, and shortening: 3.632517e-03
RS BER with
erasures: 1.851795e-06
erasures and punctures: 4.289038e-05
erasures, punctures, and shortening: 1.028213e-04
Further Exploration
You can experiment with these systems by running them over a loop of Eb/N0 values and generating a BER curve for them. You can then compare their performance against a theoretical 64-QAM/RS system without erasures, punctures, or shortening. Use BERTool to generate the theoretical BER curves.
close_system(model_e,0); close_system(model_ep,0); close_system(model_eps,0);
See Also
Binary-Input RS Encoder | Integer-Input RS Encoder | Binary-Output RS Decoder | Integer-Output RS Decoder
