Numeric Model of SISO Feedback Loop
This example shows how to interconnect numeric LTI models representing multiple system components to build a single numeric model of a closed-loop system, using model arithmetic and interconnection commands.
Construct a model of the following single-loop control system.
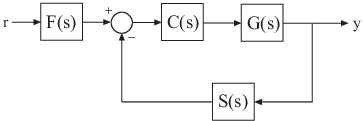
The feedback loop includes a plant G(s), a controller C(s), and a representation of sensor dynamics, S(s). The system also includes a prefilter F(s).
Create model objects representing each of the components.
G = zpk([],[-1,-1],1); C = pid(2,1.3,0.3,0.5); S = tf(5,[1 4]); F = tf(1,[1 1]);
The plant G is a zero-pole-gain (
zpk) model with a double pole at s = –1. Model object C is a PID controller. The models F and S are transfer functions.Connect the controller and plant models.
H = G*C;
To combine models using the multiplication operator
*, enter the models in reverse order compared to the block diagram.Construct the unfiltered closed-loop response .
T = feedback(H,S);
Caution
Do not use model arithmetic to construct
Talgebraically:T = H/(1+H*S)
This computation duplicates the poles of
H, which inflates the model order and might lead to computational inaccuracy.Construct the entire closed-loop system response from r to y.
T_ry = T*F;
T_ry is a Numeric LTI Model representing
the aggregate closed-loop system. T_ry does not
keep track of the coefficients of the components G, C, F,
and S.
You can operate on T_ry with any Control System Toolbox™ control
design or analysis commands.
See Also
connect | feedback | series | parallel
Related Examples
- Control System Model with Both Numeric and Tunable Components
- Multi-Loop Control System
- MIMO Control System with Fixed and Tunable Components
