Making Quality Measurements
What Do You Measure?
For most data acquisition applications, you need to measure the signal produced by a sensor at a specific rate.
In many cases, the sensor signal is a voltage level that is proportional to the physical phenomena of interest (for example, temperature, pressure, or acceleration). If you are measuring slowly changing (quasi-static) phenomena like temperature, a slow sampling rate usually suffices. If you are measuring rapidly changing (dynamic) phenomena like vibration or acoustic measurements, a fast sampling rate is required.
To make high-quality measurements, you should follow these rules:
Maximize the precision and accuracy
Minimize the noise
Match the sensor range to the A/D range
Accuracy and Precision
Whenever you acquire measured data, you should make every effort to maximize its accuracy and precision. The quality of your measurement depends on the accuracy and precision of the entire data acquisition system, and can be limited by such factors as board resolution or environmental noise.
In general terms, the accuracy of a measurement determines how close the measurement comes to the true value. Therefore, it indicates the correctness of the result. The precision of a measurement reflects how exactly the result is determined without reference to what the result means. The relative precision indicates the uncertainty in a measurement as a fraction of the result.
For example, suppose you measure a table top with a meter stick and find its length to be 1.502 meters. This number indicates that the meter stick (and your eyes) can resolve distances down to at least a millimeter. Under most circumstances, this is considered to be a fairly precise measurement with a relative precision of around 1/1500. However, suppose you perform the measurement again and obtain a result of 1.510 meters. After careful consideration, you discover that your initial technique for reading the meter stick was faulty because you did not read it from directly above. Therefore, the first measurement was not accurate.
Precision and accuracy are illustrated below.
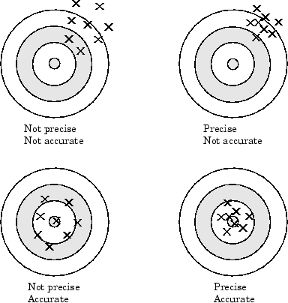
For analog input subsystems, accuracy is usually limited by calibration errors while precision is usually limited by the A/D converter. Accuracy and precision are discussed in more detail below.
Accuracy
Accuracy is defined as the agreement between a measured quantity and the true value of that quantity. Every component that appears in the analog signal path affects system accuracy and performance. The overall system accuracy is given by the component with the worst accuracy.
For data acquisition hardware, accuracy is often expressed as a percent or a fraction of the least significant bit (LSB). Under ideal circumstances, board accuracy is typically ±0.5 LSB. Therefore, a 12 bit converter has only 11 usable bits.
Many boards include a programmable gain amplifier, which is located just before the converter input. To prevent system accuracy from being degraded, the accuracy and linearity of the gain must be better than that of the A/D converter. The specified accuracy of a board is also affected by the sampling rate and the settling time of the amplifier. The settling time is defined as the time required for the instrumentation amplifier to settle to a specified accuracy. To maintain full accuracy, the amplifier output must settle to a level given by the magnitude of 0.5 LSB before the next conversion, and is on the order of several tenths of a millisecond for most boards.
Settling time is a function of sampling rate and gain value. High rate, high gain configurations require longer settling times while low rate, low gain configurations require shorter settling times.
Precision
The number of bits used to represent an analog signal determines the precision (resolution) of the device. The more bits provided by your board, the more precise your measurement will be. A high precision, high resolution device divides the input range into more divisions thereby allowing a smaller detectable voltage value. A low precision, low resolution device divides the input range into fewer divisions thereby increasing the detectable voltage value.
The overall precision of your data acquisition system is usually determined by the A/D converter, and is specified by the number of bits used to represent the analog signal. Most boards use 12 or 16 bits. The precision of your measurement is given by:
The precision in volts is given by:
For example, if you are using a 12 bit A/D converter configured for a 10 volt range, then
This means that the converter can detect voltage differences at the level of 0.00244 volts (2.44 mV).
How Are Range, Gain, and Measurement Precision Related?
When you configure the input range and gain of your analog input subsystem, the end result should maximize the measurement resolution and minimize the chance of an overrange condition. The actual input range is given by the formula:
The relationship between gain, actual input range, and precision for a unipolar and bipolar signal having an input range of 10 V is shown below.
Relationship Between Input Range, Gain, and Precision
Input Range | Gain | Actual Input Range | Precision (12 Bit A/D) |
|---|---|---|---|
0 to 10 V | 1.0 | 0 to 10 V | 2.44 mV |
2.0 | 0 to 5 V | 1.22 mV | |
5.0 | 0 to 2 V | 0.488 mV | |
10.0 | 0 to 1 V | 0.244 mV | |
-5 to 5 V | 0.5 | -10 to 10 V | 4.88 mV |
1.0 | -5 to 5 V | 2.44 mV | |
2.0 | -2.5 to 2.5 V | 1.22 mV | |
5.0 | -1.0 to 1.0 V | 0.488 mV | |
10.0 | -0.5 to 0.5 V | 0.244 mV |
As shown in the table, the gain affects the precision of your measurement. If you select a gain that decreases the actual input range, then the precision increases. Conversely, if you select a gain that increases the actual input range, then the precision decreases. This is because the actual input range varies but the number of bits used by the A/D converter remains fixed.
Note
With Data Acquisition Toolbox™ software, you do not have to specify the range and gain. Instead, you simply specify the actual input range desired.
Noise
Noise is considered to be any measurement that is not part of the phenomena of interest. Noise can be generated within the electrical components of the input amplifier (internal noise), or it can be added to the signal as it travels down the input wires to the amplifier (external noise). Techniques that you can use to reduce the effects of noise are described below.
Removing Internal Noise
Internal noise arises from thermal effects in the amplifier. Amplifiers typically generate a few microvolts of internal noise, which limits the resolution of the signal to this level. The amount of noise added to the signal depends on the bandwidth of the input amplifier.
To reduce internal noise, you should select an amplifier with a bandwidth that closely matches the bandwidth of the input signal.
Removing External Noise
External noise arises from many sources. For example, many data acquisition experiments are subject to 60 Hz noise generated by AC power circuits. This type of noise is referred to as pick-up or hum, and appears as a sinusoidal interference signal in the measurement circuit. Another common interference source is fluorescent lighting. These lights generate an arc at twice the power line frequency (120 Hz).
Noise is added to the acquisition circuit from these external sources because the signal leads act as aerials picking up environmental electrical activity. Much of this noise is common to both signal wires. To remove most of this common-mode voltage, you should
Configure the input channels in differential mode. Refer to Channel Configuration for more information about channel configuration.
Use signal wires that are twisted together rather than separate.
Keep the signal wires as short as possible.
Keep the signal wires as far away as possible from environmental electrical activity.
Filtering
Filtering also reduces signal noise. For many data acquisition applications, a low-pass filter is beneficial. As the name suggests, a low-pass filter passes the lower frequency components but attenuates the higher frequency components. The cut-off frequency of the filter must be compatible with the frequencies present in the signal of interest and the sampling rate used for the A/D conversion.
A low-pass filter that's used to prevent higher frequencies from introducing distortion into the digitized signal is known as an antialiasing filter if the cut-off occurs at the Nyquist frequency. That is, the filter removes frequencies greater than one-half the sampling frequency. These filters generally have a sharper cut-off than the normal low-pass filter used to condition a signal. Antialiasing filters are specified according to the sampling rate of the system and there must be one filter per input signal.
Matching the Sensor Range and A/D Converter Range
When sensor data is digitized by an A/D converter, you must be aware of these two issues:
The expected range of the data produced by your sensor. This range depends on the physical phenomena you are measuring and the output range of the sensor.
The range of your A/D converter. For many devices, the hardware range is specified by the gain and polarity.
You should select the sensor and hardware ranges such that the maximum precision is obtained, and the full dynamic range of the input signal is covered.
For example, suppose you are using a microphone with a dynamic range of 20 dB to 140 dB and an output sensitivity of 50 mV/Pa. If you are measuring street noise in your application, then you might expect that the sound level never exceeds 80 dB, which corresponds to a sound pressure magnitude of 200 mPa and a voltage output from the microphone of 10 mV. Under these conditions, you should set the input range of your data acquisition card for a maximum signal amplitude of 10 mV, or a little more.
How Fast Should a Signal Be Sampled?
Whenever a continuous signal is sampled, some information is lost. The key objective is to sample at a rate such that the signal of interest is well characterized and the amount of information lost is minimized.
If you sample at a rate that is too slow, then signal aliasing can occur. Aliasing can occur for both rapidly varying signals and slowly varying signals. For example, suppose you are measuring temperature once a minute. If your acquisition system is picking up a 60-Hz hum from an AC power supply, then that hum will appear as constant noise level if you are sampling at 30 Hz.
Aliasing occurs when the sampled signal contains frequency components greater than one-half the sampling rate. The frequency components could originate from the signal of interest in which case you are undersampling and should increase the sampling rate. The frequency components could also originate from noise in which case you might need to condition the signal using a filter. The rule used to prevent aliasing is given by the Nyquist theorem, which states that
An analog signal can be uniquely reconstructed, without error, from samples taken at equal time intervals.
The sampling rate must be equal to or greater than twice the highest frequency component in the analog signal. A frequency of one-half the sampling rate is called the Nyquist frequency.
However, if your input signal is corrupted by noise, then aliasing can still occur.
For example, suppose you configure your A/D converter to sample at a rate of 4 samples per second (4 S/s or 4 Hz), and the signal of interest is a 1 Hz sine wave. Because the signal frequency is one-fourth the sampling rate, then according to the Nyquist theorem, it should be completely characterized. However, if a 5 Hz sine wave is also present, then these two signals cannot be distinguished. In other words, the 1 Hz sine wave produces the same samples as the 5 Hz sine wave when the sampling rate is 4 S/s. The following diagram illustrates this condition.
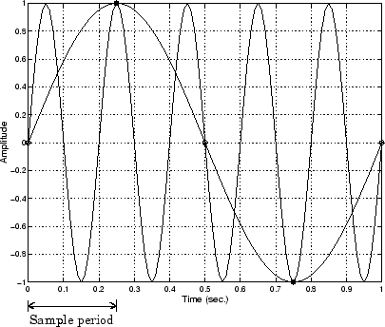
In a real-world data acquisition environment, you might need to condition the signal by filtering out the high frequency components.
Even though the samples appear to represent a sine wave with a frequency of one-fourth the sampling rate, the actual signal could be any sine wave with a frequency of:
where n is zero or any positive integer. For this example, the actual signal could be at a frequency of 3 Hz, 5 Hz, 7 Hz, 9 Hz, and so on. The relationship 0.25 × (sampling rate) is called the alias of a signal that might be at another frequency. In other words, aliasing occurs when one frequency assumes the identity of another frequency.
If you sample the input signal at least twice as fast as the highest frequency component, then that signal might be uniquely characterized, but this rate would not mimic the waveform very closely. As shown below, to get an accurate picture of the waveform, you need a sampling rate of roughly 10 to 20 times the highest frequency.
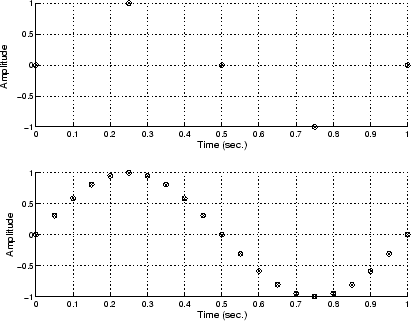
As shown in the top figure, the low sampling rate produces a sampled signal that appears to be a triangular waveform. As shown in the bottom figure, a higher fidelity sampled signal is produced when the sampling rate is higher. In the latter case, the sampled signal actually looks like a sine wave.
How Can Aliasing Be Eliminated?
The primary considerations involved in antialiasing are the sampling rate of the A/D converter and the frequencies present in the sampled data. To eliminate aliasing, you must
Establish the useful bandwidth of the measurement.
Select a sensor with sufficient bandwidth.
Select a low-pass antialiasing analog filter that can eliminate all frequencies exceeding this bandwidth.
Sample the data at a rate at least twice that of the filter's upper cutoff frequency.
