Wavelet Reconstruction and Noise Reduction
This example uses the Dyadic Analysis Filter Bank and Dyadic Synthesis Filter Bank blocks to show both the perfect reconstruction property of wavelets and an application for noise reduction.
Open the Operation block dialog and select either Remove noise or Perfect reconstruction. The selection will enable the corresponding enabled subsystem.
Wavelet Reconstruction subsystem shows an Analysis Filter Bank followed by the Wavelet Reconstruction subsystem. The net effect of these two operations is perfect reconstruction of the input signal.
Opening the Noise Reduction subsystem shows the same wavelet blocks but with a soft threshold applied to the transformed signal bands. By attenuating the higher frequency bands, the high frequency noise is reduced. You can adjust the threshold levels to see the effects of attenuation on the denoising characteristics of the system.
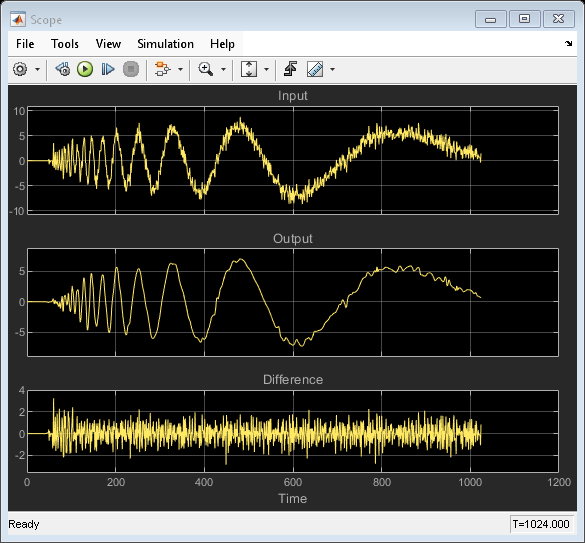
Run the example to view the input and output signals and the difference between them. Note that for perfect reconstruction, the difference appears to be zero. However, due to numerical effects, there is a small difference that can be seen in the display of the running RMS display.

For floating-point sample-based version, open dspwaveletModel.slx. For floating-point frame-based version, open dspwavelet_frameModel.slx. For fixed-point sample-based version, open dspwavelet_fixptModel.slx. To find these models, open this example in MATLAB®, click on the Open Script button in the example. The example script opens and you can find all the models in the current working directory of MATLAB.
