dsp.Interpolator
(Removed) Linear or polyphase FIR interpolation
dsp.Interpolator has been removed. Use dsp.FIRInterpolator, interp1 instead. For more information, see
Compatibility Considerations.
Description
The dsp.Interpolator
System object™ interpolates values between real-valued input samples using linear or polyphase
FIR interpolation. Specify which values to interpolate by providing a vector of interpolation
points. An interpolation point of 1 refers to the first sample in the input. To interpolate
the value halfway between the second and third sample in the input, specify an interpolation
point of 2.5. Interpolation points that are not within the valid range are replaced with the
closest value in the valid range.
To interpolate a real-valued input signal:
Create the
dsp.Interpolatorobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Creation
Description
interp = dsp.Interpolatorinterp, to interpolate values between real-valued
input samples using linear interpolation.
interp = dsp.Interpolator(Name,Value)interp, with each specified property set to the
specified value. Enclose each property name in single quotes.
Example: interp = dsp.Interpolator('InterpolationPointsSource','Input port')
Properties
Unless otherwise indicated, properties are nontunable, which means you cannot change their
values after calling the object. Objects lock when you call them, and the
release function unlocks them.
If a property is tunable, you can change its value at any time.
For more information on changing property values, see System Design in MATLAB Using System Objects.
InterpolationPointsSource — Source of interpolation points
'Property' (default) | 'Input port'
Method to specify the interpolation points, specified as one of the following:
'Property'— Specify the interpolation points through the InterpolationPoints property.'Input port'— Pass the interpolation points as an input to the System object algorithm.
InterpolationPoints — Interpolation points
[1.1;4.8;2.67;1.6;3.2] (default) | vector | matrix | N-D array
Interpolation points, specified as a vector, matrix, or an N-D
array. The valid range of the values in the interpolation vector is from 1 to the number
of samples in each channel of the input. If you specify interpolation points outside the
valid range, the object clips the point to the nearest point in the
valid range. For example, if the input is [2;3.1;-2.1], the valid
range of interpolation points is from 1 to 3. If
you specify a [-1;1.5;2;2.5;3;3.5] vector of interpolation points,
the interpolator object clips -1 to 1 and
3.5 to 3. This clipping results in the
interpolation points [1 1.5 2 2.5 3 3].
For details on the dimension of the interpolation points array and how that influences the dimension of the output, see the tables in the ipts input of the System object.
Tunable: Yes
Dependencies
This property applies only when you set the InterpolationPointsSource property to
'Property'.
Method — Interpolation method
'Linear' (default) | 'FIR'
Interpolation method, specified as one of the following:
'Linear'–– The object interpolates data values by assuming that the data varies linearly between samples taken at adjacent sample times.'FIR'–– The object uses polyphase interpolation to replace filtering (convolution) at the upsampled rate with a series of convolutions at the lower rate. If the input has insufficient low-rate samples to perform FIR interpolation, the interpolator object performs linear interpolation. For more details, see the FilterHalfLength property.
FilterHalfLength — Half-length of interpolation filter
3 (default) | integer scalar greater than 0
For a filter half-length of P, the polyphase FIR subfilters have length 2P. FIR interpolation always requires 2P low-rate samples for every interpolation point.
If the interpolation point does not correspond to a low-rate sample, FIR interpolation requires P low-rate samples below and P low-rate samples above the interpolation point.
If the interpolation point corresponds to a low-rate sample, the 2P-sample requirement includes the low-rate sample.
If the input has less than 2P neighboring low-rate samples, the interpolator object uses linear interpolation.
For example, for an input [1 4 1 4 1 4 1 4], upsampling by a
factor of 4 results in equally spaced interpolation points, InterP =
[1:0.25:8]. The points InterP(9:12) are [3.0
3.25 3.5 3.75]. If you set FilterHalfLength to 2,
interpolating at these points uses the 4 low-rate samples from the input with indices
(2,3,4,5). If you set FilterHalfLength to 4,
the interpolator object uses linear interpolation, because the input does not have
enough low-rate samples to perform FIR interpolation.
The longer the FilterHalfLength property, the better the
quality of the interpolation. However, increasing the filter half-length increases
computation time and requires more low-rate samples below and above the interpolation
point. In general, setting the FilterHalfLength property between 4
and 6 provides a reasonably accurate interpolation.
Dependencies
This property applies only when you set the Method property to 'FIR'.
InterpolationPointsPerSample — Upsampling factor
3 (default) | integer scalar greater than 0
Upsampling factor, specified as an integer scalar greater than 0. An upsampling
factor of L inserts L – 1 zeros between low-rate
samples. Interpolation results from filtering the upsampled sequence with a lowpass
anti-imaging filter. The interpolator object uses a polyphase FIR implementation with
InterpolationPointsPerSample subfilters of length
2P, where P is the value you specify in the
FilterHalfLength property. For nL
low-rate samples in the upsampled input, where n=1,2,..., the
interpolator object uses exactly one of the
InterpolationPointsPerSample subfilters to interpolate at the
points nL+i/L, where i = 0, 1, 2, …,
L – 1.
If you specify interpolation points that do not correspond to a polyphase
subfilter, the object rounds the point down to the nearest interpolation point
associated with a polyphase subfilter. Suppose you set the
InterpolationPointsPerSample property to 4 and interpolate at the
points [3 3.2 3.4 3.6 3.8]. The interpolator object uses the first
polyphase subfilter for the points [3.0 3.2], the second subfilter
for the point 3.4, the third subfilter for the point
3.6, and the fourth subfilter for the point
3.8.
Dependencies
This property applies only when you set the Method property to 'FIR'.
Bandwidth — Normalized input bandwidth
0.5 (default) | real scalar greater than 0 and less than or equal to 1
Bandwidth to which the interpolated output samples must be constrained, specified as
a real scalar greater than 0 and less than or equal to 1. A value of 1 equals the
Nyquist frequency, or half the sampling frequency, Fs. Use this
property to take advantage of the bandlimited frequency content of the input. For
example, if the input signal does not have frequency content above
Fs/4, you can specify a value of 0.5 for the
Bandwidth property.
Dependencies
This property applies only when you set the Method property to 'FIR'.
Usage
Description
interpOut = interp(input)interpOut, of the input vector or
matrix input, as specified in the InterpolationPoints property. Each column of
input is treated as an independent channel of the input.
interpOut = interp(input,ipts)ipts.
To specify the interpolation points, set the InterpolationPointsSource property to 'Input
port'.
t = 0:.0001:.0511; x = sin(2*pi*20*t); x1 = x(1:50:end); ipts = 1:0.1:length(x1); interp = dsp.Interpolator('InterpolationPointsSource','Input port'); interpOut = interp(x1',ipts');
Input Arguments
input — Data input
vector | matrix | N-D array
Input that is interpolated by the object, specified as a vector, matrix, or N-D array.
Example: t = 0:0.0001:0.0511; input = sin(2*pi*20*t);
Data Types: single | double
ipts — Interpolation points
vector | matrix | N-D array
Interpolation array IPts, specified as a vector, matrix, or N-D array. The interpolation array represents the points in time at which to interpolate values of the input signal. An entry of 1 in IPts refers to the first sample of the input, an entry of 2.5 refers to the sample halfway between the second and third input sample, and so on. In most cases, when IPts is a vector, it can be of any length.
Valid values in the interpolation array
IPts range from 1 to the number of samples
in each channel of the input. For instance, given a length-5 input vector
D, all entries of IPts
must range from 1 to 5. IPts cannot contain
entries such as 7 or –9, because D does not have a seventh or ninth
entry.
The algorithm replaces any out-of-range values in IPts with the closest value in the valid range (from 1 to the number of input samples). Then it performs the interpolation using the clipped version of IPts.
Consider the following input data and interpolation points vector:
D = [11 22 33 44]'IPts = [10 2.6 -3]'
Because D has four samples, valid interpolation points range
from 1 to 4. The algorithm clips interpolation point 10 down to to 4 and the point –3
up to 1. The result is the clipped interpolation vector
IPtsClipped = [4 2.6 1]'.
Depending on the dimension of the input and the dimension of IPts, the algorithm applies IPts to the input in one of the following ways:
If IPts is an array, the object applies IPts across the first dimension of an N-D array, resulting in an N-D array output.
If IPts is a vector, the object applies IPts to each input vector (as if the input vector were a single channel), resulting in a vector output with the same orientation as the input (row or column).
The following tables summarize how the object applies the interpolation array IPts to all the possible types of inputs. The table also shows the resulting output dimensions.
This table describes the behavior when
InterpolationPointsSource is set to
'Property'.
| Input Dimensions | Valid Dimensions of Interpolation Array IPts | How Object Applies IPts to Input | Output Dimensions |
|---|---|---|---|
M-by-N-by-K matrix | P-by-1 column | Applies IPts to the first dimension of the input | P-by-N-by-K array |
P-by-N-by-K matrix | Applies each column element of IPts to the corresponding column of the input matrix | P-by-N-by-K array | |
M-by-N matrix | 1-by-N row | Applies each column element of IPts to the corresponding column of the input matrix | 1-by-N row |
P-by-1 column | Applies IPts to each input column | P-by-N matrix | |
P-by-N matrix | Applies the columns of IPts to the corresponding columns of the input matrix | ||
M-by-1 column | 1-by-P row (the algorithm treats IPts as a column) | Applies IPts to the input column | P-by-1 column |
P-by-1 column | |||
1-by-N row (not recommended) | 1-by-N row | Not applicable. Object copies input vector. | 1-by-N row, a copy of the input vector |
P-by-1 column | P-by-N matrix, where each row is a copy of the input vector | ||
P-by-N matrix |
This table describes the behavior when
InterpolationPointsSource is set to 'Input
port'.
| Input Dimensions | Valid Dimensions of Interpolation Array IPts | How Object Applies IPts to Input | Output Dimensions |
|---|---|---|---|
M-by-N-by-K matrix | Column vector of length P | Applies IPts to the first dimension of the input | P-by-N-by-K array |
P-by-N-by-K matrix | Applies each column element of IPts to the corresponding column of the input matrix | P-by-N-by-K array | |
M-by-N matrix | 1-by-N row | Applies each column element of IPts to the corresponding column of the input matrix | 1-by-N row |
P-by-1 column | Applies IPts to each input column | P-by-N matrix | |
P-by-N matrix | Applies the columns of IPts to the corresponding columns of the input matrix | ||
M-by-1 column | 1-by-P row | Applies IPts to the input column | P-by-1 column |
P-by-1 column | |||
1-by-N row (not recommended) | 1-by-N row | Not applicable. Object copies input vector. | 1-by-N row, a copy of the input vector |
P-by-1 column | P-by-N matrix, where each row is a copy of the input vector | ||
P-by-N matrix |
Example: ipts = [1:10];
Data Types: single | double
Output Arguments
interpOut — Interpolated sequence
vector | matrix | N-D array
Interpolated sequence, returned as a vector, matrix, or N-D array. The dimension of the output depends on the dimensions of the input and the interpolation points array. For more details on the dimensions, see the tables in ipts.
Data Types: single | double
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
Examples
Interpolate a Sum of Sinusoids
Interpolate a sum of sinusoids with FIR interpolation, and with 'Input port' as the source of interpolation points.
Fs = 1000; t = 0:(1/Fs):0.1-(1/Fs); x = cos(2*pi*50*t)+0.5*sin(2*pi*100*t); x1 = x(1:4:end); I = 1:(1/4):length(x1); interp = dsp.Interpolator('Method','FIR',... 'FilterHalfLength',3,'InterpolationPointsSource','Input Port'); y = interp(x1',I'); stem(I,y,'r'); hold on; axis([0 25 -2 2]); stem(x1,'b','linewidth',2); legend('Interpolated Signal','Original',... 'Location','Northeast');
Algorithms
Linear Interpolation Mode
In the linear interpolation mode, the algorithm interpolates data values by assuming that the data varies linearly between samples taken at adjacent sample times.
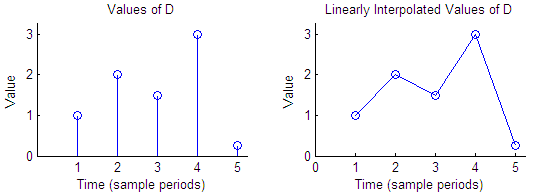
Suppose the input signal is D = [1 2 1.5 3 0.25]' . The left plot
shows the samples in D and the right plot shows the linearly interpolated
values between the samples in D.
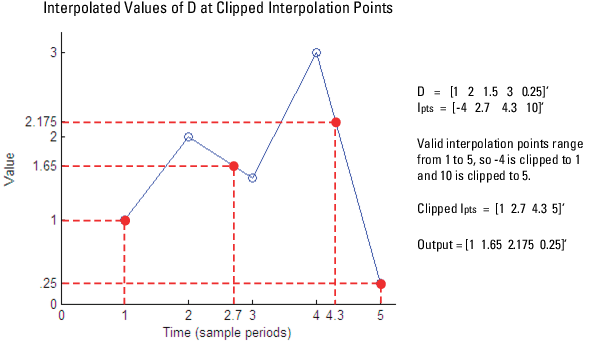
When the interpolation points are out of range, the algorithm clips the invalid
interpolation points. Consider an input signal, D = [1 2 1.5 3 0.25]' ,
and an interpolation vector, IPts = [-4 2.7 4.3
10]'. The interpolated output is given by [1 1.65 2.175
0.25]'.
FIR Interpolation Mode
In the FIR interpolation mode, the algorithm interpolates data values using an FIR interpolation filter. The FIR filter is implemented using a polyphase structure. A polyphase implementation splits the lowpass FIR filter impulse response into a number of different subfilters.
Let L represent the number of interpolation points per sample, or the upsampling factor. Let P represent the half length of the polyphase subfilters. Indexing from zero, if h(n) is the impulse response of the FIR filter, the kth subfilter is:
The table describes the decomposition of an 18-coefficient FIR filter into 3 polyphase subfilters of length 6, the defaults for the FIR interpolator object.
| Coefficients | Polyphase Subfilter |
|---|---|
| h(0),h(3),h(6), ..., h(15) | h0(n) |
| h(1),h(4),h(7), ..., h(16) | h1(n) |
| h(2),h(5),h(8), ..., h(17) | h2(n) |
An upsampling factor of L inserts L – 1 zeros between low-rate samples. Interpolation results from filtering the upsampled sequence with a lowpass anti-imaging filter.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
Usage notes and limitations:
See System Objects in MATLAB Code Generation (MATLAB Coder).
Version History
Introduced in R2012aR2023a: dsp.Interpolator
System object has been removed
The dsp.Interpolator
System object has been removed. Use dsp.FIRInterpolator, interp1 instead.
Update Code
This table shows how to update existing code to use the replacement features.
| Discouraged Usage | Replacement using dsp.FIRInterpolator |
|---|---|
Linear interpolation Create the input signal. n = 0:11; x = sin(2*pi*n/length(n)); Create
the L = 10; t = (n(1):1/L:n(end)+1-1/L)+1/L; interpolator = dsp.Interpolator(InterpolationPoints=t'); y = interpolator(x'); | Linear interpolation Create a triangle interpolation filter. This filter yields a linear interpolation template. Apply this filter to the input signal. hLin = triang(2*L-1); firInterpolator = dsp.FIRInterpolator(L,hLin); yf = firInterpolator(x'); Plot and compare the interpolated outputs. scatter(t,y); hold on; scatter(t,yf,'+'); hold off; legend('dsp.Interpolator','dsp.FIRInterpolator'); |
FIR interpolation Create the input signal. n = 1:60; x = sin(10*pi*n/length(n))'; Create
the L = 5; P = 6; t = 1:1/L:length(x); intr = dsp.Interpolator(Method='FIR',... FilterHalfLength=P,... InterpolationPoints=t',... InterpolationPointsPerSample=L); y_int = intr(x); | FIR interpolation Determine
the FIR coefficients of the interpolator to use with
FIRcoeffs = intfilt(L,P,0.5); hFIR = [zeros(2*L-mod(length(FIRcoeffs),2*L),1); FIRcoeffs(:)]; Create
a firintr = dsp.FIRInterpolator(L,hFIR); y_firint = firintr(x); Plot and compare the input signal and the interpolated outputs. i0 = floor(length(hFIR)/2); % Latency tfir = (1:1/L:length(x)+1-1/L) - i0/L; figure; hold on; scatter(n,x,50,'filled','Dk') scatter(t,y_int,50,'red'); scatter(tfir,y_firint,50,'bx'); legend('Low rate input','dsp.Interpolator',... 'dsp.FIRInterpolator','Location','Northeast'); |
| Discouraged Usage | Replacement using interp1 |
|---|---|
Create the input signal. n = (1:60); x = sin(10*pi*n/length(n))'; For
uniformly spaced interpolation points, use this t = 1:1/10:60; For
nonuniformly spaced interpolation points, use this t = sort(n(1)+(n(end)-n(1))*rand(1,500)); Create
the intr = dsp.Interpolator(Method='Linear',InterpolationPoints=t');
y_int = intr(x);
| Pass the input signal to the y_interp1 = interp1(n,x,t); Plot and compare the input signal and the interpolated outputs. figure; hold on; scatter(1+(0:length(x)-1),x,50,'filled','Dk') scatter(t,y_int,50,'red'); scatter(t,y_interp1,50,'blue','x'); legend('Low rate input','dsp.Interpolator',... 'interp1','Location','Northeast'); |
R2021b: dsp.Interpolator System object will be removed
dsp.Interpolator
System object will be removed in a future release. Use dsp.FIRInterpolator, interp1 instead.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)