Fast Block LMS Filter
Compute output, error, and weights using least mean squares (LMS) adaptive algorithm
Libraries:
DSP System Toolbox /
Filtering /
Adaptive Filters
Description
The Fast Block LMS Filter block implements an adaptive least mean squares (LMS) filter, where the adaptation of the filter weights occurs once for every block of data samples. The block estimates the filter weights (also known as the coefficients) needed to minimize the error e(n) between the output signal y(n) and the desired signal d(n).
The Fast Block LMS Filter block uses the Block LMS Filter equations to estimate the filter weights. For more information, see Algorithms. The Fast Block LMS Filter block implements the convolution operation involved in the calculations of the filtered output and the weight update function in the frequency domain using the FFT algorithm used in the Frequency-Domain FIR Filter block.
For more information on adaptive filters, see Overview of Adaptive Filters and Applications.
Ports
Input
Input — Input signal
scalar | column vector
Specify the input signal you want to filter as a scalar or a column vector.
The input signal and the desired signal must have the same size, data type, and complexity.
The input frame length (number of rows in the input) must be an integer multiple of the value you specify in the Block size parameter.
Data Types: single | double
Complex Number Support: Yes
Desired — Desired signal
scalar | column vector
Specify the signal you want to model as a scalar or a column vector. The LMS filter adapts its coefficients to minimize the error and converge the input signal to the desired signal as closely as possible.
The input signal and the desired signal must have the same size, data type, and complexity.
Data Types: single | double
Complex Number Support: Yes
Step-size — Adaptation step size
nonnegative scalar
Specify the adaptation step size as a nonnegative scalar. The data type of the step size input must match the data type of the input signal and the desired signal.
A small step size ensures a small steady state error between the output signal and the desired signal. If the step size is small, the convergence speed of the filter decreases. To improve the convergence speed, increase the step size. Note that if the step size is large, the filter can become unstable.
Dependencies
To enable this port, set Specify step size
via to 'Input
port'.
Data Types: single | double
Adapt — Specify the block to update filter weights
scalar
Specify the block to update filter weights. If the value of this input is nonzero, the block continuously updates the filter weights. If the value of this input is zero, the filter weights remain at their current values.
Dependencies
To enable this port, select the Adapt port check box.
Data Types: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32 | Boolean
Reset — Reset signal
scalar
Specify the reset signal as a scalar signal. When you want to reset the value of the filter weights to their initial values, use the Reset port parameter. The block resets the filter weights whenever a reset event is detected at the Reset port. The reset signal rate must be the same rate as the data signal input.
To enable the Reset port, select one of the following from the Reset port list:
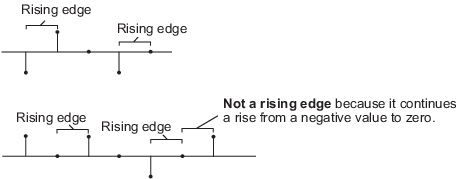
Rising edge— Triggers a reset operation when the Reset input does one of the following:Rises from a negative value to a positive value or zero
Rises from zero to a positive value, where the rise is not a continuation of a rise from a negative value to zero
See the following figure:
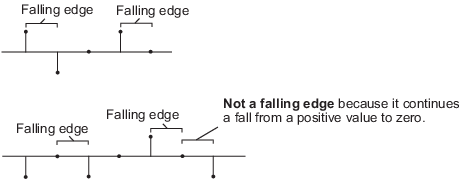
Falling edge— Triggers a reset operation when the Reset input does one of the following:Falls from a positive value to a negative value or zero
Falls from zero to a negative value, where the fall is not a continuation of a fall from a positive value to zero
See the following figure:
Either edge— Triggers a reset operation when the Reset input is aRising edgeorFalling edgeNon-zero sample— Triggers a reset operation at each sample time that the Reset input is not zero
To disable the reset port, set Reset port to
None.
Dependencies
To enable this port, set Reset port to any
option other than None.
Data Types: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32 | Boolean
Output
Output — Filtered signal
scalar | column vector
Filtered signal, returned as a scalar or a column vector. The block adapts its filter coefficients to converge the input signal to match the desired signal. The filter outputs the converged signal.
Data Types: single | double
Complex Number Support: Yes
Error — Difference between output and desired signal
scalar | column vector
Difference between the filtered signal and the desired signal, returned as a scalar or a column vector. The objective of the LMS filter is to minimize this error. The block adapts its coefficients to converge towards optimal filter coefficients that produce an output signal that matches closely with the desired signal.
Data Types: single | double
Complex Number Support: Yes
Wts — Adaptive filter weights
scalar | column vector
Weights of the LMS filter, returned as a column vector of length equal to the value you specify in the Filter length parameter. For each iteration, the block outputs the current updated filter weights from this port.
The data type of the filter weights matches the data type of the filtered signal.
Dependencies
To enable this port, select the Output filter weights check box.
Data Types: single | double
Complex Number Support: Yes
Parameters
Filter length — Length of FIR filter coefficients vector
32 (default) | positive integer
Specify the length of the FIR filter coefficients vector as a positive integer. The sum of filter length and block length must be a power of 2.
Block size — Number of samples acquired before weight adaptation
32 (default) | positive integer
Specify the number of samples of the input signal to acquire before the block updates the filter weights as a positive integer. The input frame length (number of rows in the input) must be an integer multiple of the value you specify in this parameter. The sum of filter length and block length must be a power of 2.
Specify step size via — Source of adaptation step size
Dialog (default) | Input port
Specify the adaptation step size through:
Dialog–– Use the Step size (mu) parameter to specify the step size in the block dialog box.Input port–– Use the Step-size input port to specify the step size.
Step-size (mu) — Step-size
0.008 (default) | nonnegative integer
Specify the adaptation step size µ as a nonnegative integer. You can specify the step size using the input port, Step-size, or enter a value in this parameter.
A small step size ensures a small steady state error between the output signal and the desired signal. If the step size is small, the convergence speed of the filter decreases. To improve the convergence speed, increase the step size. Note that if the step size is large, the filter can become unstable.
Tunable: Yes
Dependencies
To enable this parameter, set the Specify step size
via parameter to
Dialog.
Leakage factor (0 to 1) — Leakage factor used in leaky LMS algorithm
1.0 (default) | scalar in the range [0, 1]
Specify the leakage factor used in the leaky LMS algorithm shown below as
a scalar in the range [0, 1], .
When the value is less than 1, the block implements a leaky LMS algorithm.
The default is 1, providing no leakage in the adapting
algorithm.
Tunable: Yes
Initial value of filter weights — Initial value of filter weights
0 (default) | scalar | vector
Specify initial values of the filter weights as a scalar or a vector of length equal to the filter length. When you specify a scalar, the block uses the scalar value to create a vector of filter weights. This vector has length equal to the filter length and all of its values are equal to the scalar value.
Adapt port — Enable Adapt port
off (default) | on
Select this check box to enable the Adapt input port. Through this port, you can specify the block to update its filter weights or to keep them at the current level. For more information, see the description of the Adapt input port.
Reset port — Enable Reset port
None (default) | Rising Edge | Falling Edge | Either Edge | Non-zero sample
Select this check box to enable the Reset input port. For more information on each of the reset options, see the description for the Reset input port.
Output filter weights — Output filter weights
on (default) | off
Select this check box to export the filter weights from the Wts port.
Block Characteristics
Data Types |
|
Direct Feedthrough |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
Zero-Crossing Detection |
|
References
[1] Hayes, M.H. Statistical Digital Signal Processing and Modeling. New York: John Wiley & Sons, 1996.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
Generated code relies on the memcpy or
memset function (string.h) under certain
conditions.
Version History
Introduced before R2006a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)
