fdesign.bandpass
Bandpass filter design specification object
Syntax
Description
The fdesign.bandpass function returns a
bandpass filter design specification object that contains
specifications for a filter such as passband frequency, stopband frequency, passband
ripple, and filter order. Use the design function to design the filter from the filter design
specifications object.
For more control options, see Filter Design Procedure. For a complete workflow, see Design a Filter in Fdesign — Process Overview.
bandpassSpecs = fdesign.bandpass
First stopband frequency set to 0.35.
First passband frequency set to 0.45.
Second passband frequency set to 0.55.
Second stopband frequency set to 0.65.
First stopband attenuation set to 60 dB.
Passband ripple set to 1dB.
Second stopband attenuation set to 60 dB.
bandpassSpecs = fdesign.bandpass(spec,value1,...,valueN)spec. After
the expression, specify a value for each option. If you do not specify values after
the spec argument, the function assumes the default
values.
bandpassSpecs = fdesign.bandpass(___,Fs)Fs
must be specified as a scalar trailing the other numerical values provided. In this
case, all frequencies in the specifications are in Hz as well.
The design specification
fdesign.bandpass('Fst1,Fp1,Fp2,Fst2,Ast1,Ap,Ast2',.4,.5,.6,.7,60,1,80)
designs the same filter as
fdesign.bandstop('Fst1,Fp1,Fp2,Fst2,Ast1,Ap,Ast2',1600,2000,2400,2800,60,1,80,8000)
bandpassSpecs = fdesign.bandpass(___,magunits)magunits can be
one of the following: 'linear', 'dB', or
'squared'. If this argument is omitted, the object assumes
the units of magnitude specification to be 'dB'. The magnitude
specifications are always converted and stored in decibels regardless of how they
were specified. If Fs is provided, magunits
must follow Fs in the input argument list.
Examples
Design Equiripple FIR Bandpass Filter
Design a constrained-band FIR equiripple filter of order 100 with a passband of [1, 1.4] kHz. Both stopband attenuation values are constrained to 60 dB. The sample rate is 10 kHz.
Create a bandpass filter design specification object using the fdesign.bandpass function and specify these design parameters.
bandpassSpecs = fdesign.bandpass('N,Fst1,Fp1,Fp2,Fst2,C',100,800,1e3,1.4e3,1.6e3,1e4);Constrain the two stopbands with a stopband attenuation of 60 dB.
bandpassSpecs.Stopband1Constrained = true; bandpassSpecs.Astop1 = 60; bandpassSpecs.Stopband2Constrained = true; bandpassSpecs.Astop2 = 60;
Design the bandpass filter using the design function. The resulting filter is a dsp.FIRFilter System object™. For details on how to apply this filter on streaming data, refer to dsp.FIRFilter.
bandpassFilt = design(bandpassSpecs,Systemobject=true)
bandpassFilt =
dsp.FIRFilter with properties:
Structure: 'Direct form'
NumeratorSource: 'Property'
Numerator: [5.5055e-04 5.4751e-05 -2.2052e-05 6.5244e-05 3.6129e-04 5.7237e-04 1.9824e-04 -9.8650e-04 -0.0025 -0.0030 -0.0014 0.0023 0.0062 0.0075 0.0040 -0.0034 -0.0109 -0.0135 -0.0082 0.0031 0.0142 0.0181 0.0119 -0.0012 ... ] (1x101 double)
InitialConditions: 0
Use get to show all properties
Visualize the frequency response of the designed filter.
filterAnalyzer(bandpassFilt)
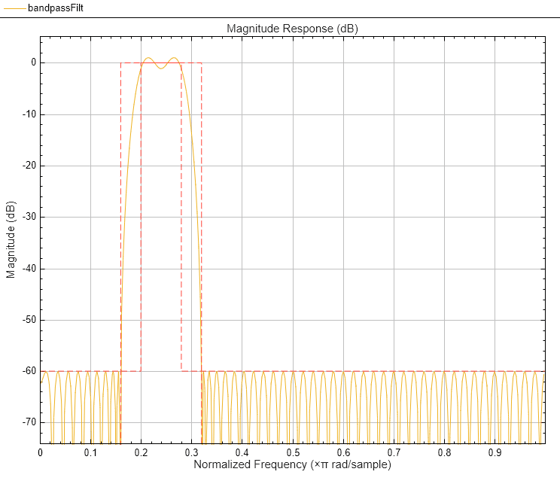
Measure the frequency response characteristics of the filter using measure. The passband ripple is slightly over 2 dB. Because the design constrains both stopbands, you cannot constrain the passband ripple.
measure(bandpassFilt)
ans = Sample Rate : 10 kHz First Stopband Edge : 800 Hz First 6-dB Point : 946.7621 Hz First 3-dB Point : 975.1807 Hz First Passband Edge : 1 kHz Second Passband Edge : 1.4 kHz Second 3-dB Point : 1.4248 kHz Second 6-dB Point : 1.4533 kHz Second Stopband Edge : 1.6 kHz First Stopband Atten. : 60.0614 dB Passband Ripple : 2.1443 dB Second Stopband Atten. : 60.0399 dB First Transition Width : 200 Hz Second Transition Width : 200 Hz
Design Butterworth IIR Bandpass Filter
Design a Butterworth IIR bandpass filter. The filter design procedure is:
Specify the filter design specifications using a
fdesignfunction.Pick a design method provided by the
designmethodsfunction.To determine the available design options to choose from, use the
designoptionsfunction.Design the filter using the
designfunction.
Construct a default bandpass filter design specification object using fdesign.bandpass.
bandpassSpecs = fdesign.bandpass
bandpassSpecs =
bandpass with properties:
Response: 'Bandpass'
Specification: 'Fst1,Fp1,Fp2,Fst2,Ast1,Ap,Ast2'
Description: {7x1 cell}
NormalizedFrequency: 1
Fstop1: 0.3500
Fpass1: 0.4500
Fpass2: 0.5500
Fstop2: 0.6500
Astop1: 60
Apass: 1
Astop2: 60
Determine the available designmethods using the designmethods function. To design a Butterworth filter, pick butter.
designmethods(bandpassSpecs,'Systemobject',true)Design Methods that support System objects for class fdesign.bandpass (Fst1,Fp1,Fp2,Fst2,Ast1,Ap,Ast2): butter cheby1 cheby2 ellip equiripple kaiserwin
When designing the filter, you can specify additional design options. View a list of options using the designoptions function. The function also shows the default design options the filter uses.
designoptions(bandpassSpecs,'butter')ans = struct with fields:
FilterStructure: {'df1sos' 'df2sos' 'df1tsos' 'df2tsos' 'cascadeallpass' 'cascadewdfallpass'}
SOSScaleNorm: 'ustring'
SOSScaleOpts: 'fdopts.sosscaling'
MatchExactly: {'passband' 'stopband'}
SystemObject: 'bool'
DefaultFilterStructure: 'df2sos'
DefaultMatchExactly: 'stopband'
DefaultSOSScaleNorm: ''
DefaultSOSScaleOpts: [1x1 fdopts.sosscaling]
DefaultSystemObject: 0
Use the design function to design the filter. Pass 'butter' and the specifications given by variable bandpassSpecs, as input arguments. Specify the 'matchexactly' design option to 'passband'.
bpFilter = design(bandpassSpecs,'butter','matchexactly','passband','SystemObject',true)
bpFilter =
dsp.SOSFilter with properties:
Structure: 'Direct form II'
CoefficientSource: 'Property'
Numerator: [7x3 double]
Denominator: [7x3 double]
HasScaleValues: true
ScaleValues: [0.1657 0.1657 0.1561 0.1561 0.1504 0.1504 0.1485 1]
Use get to show all properties
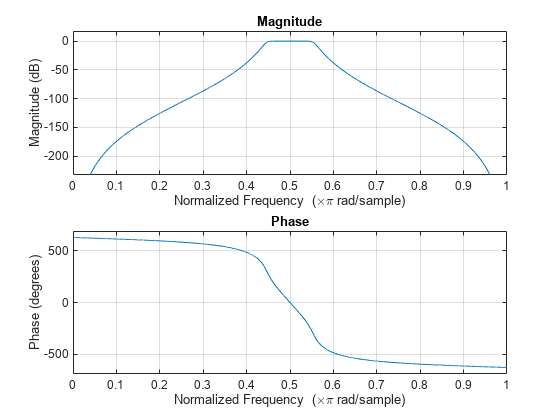
Visualize the frequency response of the designed filter.
freqz(bpFilter)
Bandpass Filtering of Sinusoids
Bandpass filter a discrete-time sine wave signal which consists of three sinusoids at frequencies, 1 kHz, 10 kHz, and 15 kHz.
Design an FIR Equiripple bandpass filter by first creating a bandpass filter design specifications object, and then designing a filter using these specifications.
Design Bandpass Filter
Create a bandpass filter design specifications object using fdesign.bandpass.
bandpassSpecs = fdesign.bandpass('Fst1,Fp1,Fp2,Fst2,Ast1,Ap,Ast2', ... 1/4,3/8,5/8,6/8,60,1,60);
List the available design methods for this object.
designmethods(bandpassSpecs)
Design Methods for class fdesign.bandpass (Fst1,Fp1,Fp2,Fst2,Ast1,Ap,Ast2): butter cheby1 cheby2 ellip equiripple kaiserwin
To design an Equiripple filter, pick 'equiripple'.
bpFilter = design(bandpassSpecs,'equiripple',Systemobject=true)bpFilter =
dsp.FIRFilter with properties:
Structure: 'Direct form'
NumeratorSource: 'Property'
Numerator: [-0.0043 -3.0812e-15 0.0136 3.7820e-15 -0.0180 -4.2321e-15 7.1634e-04 4.0993e-15 0.0373 -4.1057e-15 -0.0579 3.7505e-15 0.0078 -3.4246e-15 0.1244 2.4753e-15 -0.2737 -8.6287e-16 0.3396 -8.6287e-16 -0.2737 ... ] (1x37 double)
InitialConditions: 0
Use get to show all properties
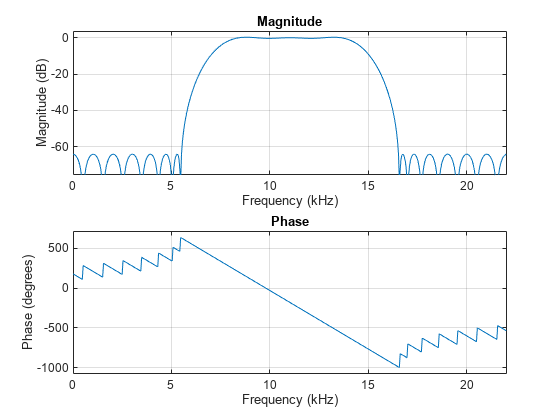
Visualize the frequency response of the designed filter.
freqz(bpFilter,[],44100)
Create Sinusoidal Signal
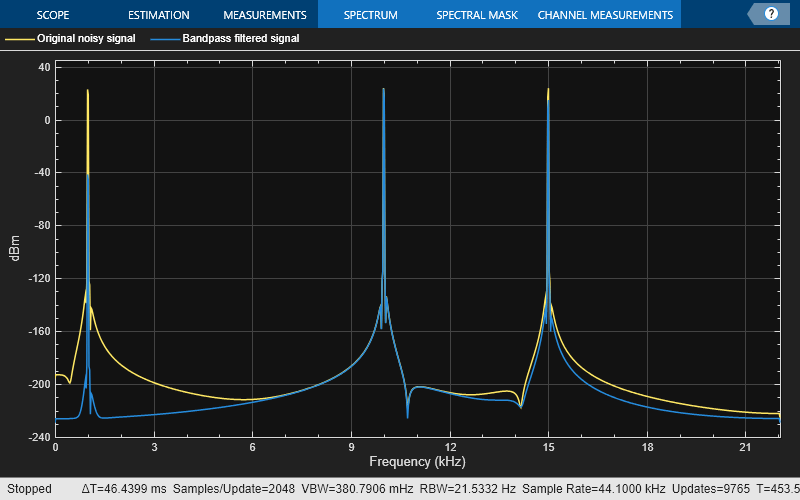
Create a signal that is a sum of three sinusoids with frequencies at 1 kHz, 10 kHz, and 15 kHz. Initialize spectrum analyzer to view the original signal and the filtered signal.
Sine1 = dsp.SineWave(Frequency=1e3,SampleRate=44.1e3,SamplesPerFrame=4000); Sine2 = dsp.SineWave(Frequency=10e3,SampleRate=44.1e3,SamplesPerFrame=4000); Sine3 = dsp.SineWave(Frequency=15e3,SampleRate=44.1e3,SamplesPerFrame=4000); SpecAna = spectrumAnalyzer(PlotAsTwoSidedSpectrum=false, ... SampleRate=Sine1.SampleRate, ... ShowLegend=true, ... YLimits=[-240,45]); SpecAna.ChannelNames = {'Original noisy signal','Bandpass filtered signal'};
Filter Sinusoidal Signal
Filter the sinusoidal signal using the bandpass filter that has been designed. View the original signal and the filtered signal in the spectrum analyzer. The tone at 1 kHz is filtered out and attenuated. The tone at 10 kHz is unaffected, and the tone at 15 kHz is mildly attenuated because it appears in the transition band of the filter.
for i = 1:5000 x = Sine1()+Sine2()+Sine3(); y = bpFilter(x); SpecAna(x,y); end release(SpecAna)
Input Arguments
spec — Specification
'Fst1,Fp1,Fp2,Fst2,Ast1,Ap,Ast2' (default) | 'N,F3dB1,F3dB2' | 'N,F3dB1,F3dB2,Ap' | ...
Specification expression, specified as one of these character vectors:
'Fst1,Fp1,Fp2,Fst2,Ast1,Ap,Ast2'(default)'N,F3dB1,F3dB2''N,F3dB1,F3dB2,Ap''N,F3dB1,F3dB2,Ast''N,F3dB1,F3dB2,Ast1,Ap,Ast2''N,F3dB1,F3dB2,BWp''N,F3dB1,F3dB2,BWst''N,Fc1,Fc2''N,Fc1,Fc2,Ast1,Ap,Ast2''N,Fp1,Fp2,Ap''N,Fp1,Fp2,Ast1,Ap,Ast2''N,Fst1,Fp1,Fp2,Fst2''N,Fst1,Fp1,Fp2,Fst2,C''N,Fst1,Fp1,Fp2,Fst2,Ap''N,Fst1,Fst2,Ast''Nb,Na,Fst1,Fp1,Fp2,Fst2'
This table describes each option that can appear in the expression.
| Specification option | Description |
|---|---|
Ap | Amount of ripple allowed in passband, specified as
Apass in dB. |
Ast | Stopband attenuation (dB), specified using
Astop. |
Ast1 | Attenuation in the first stopband (dB), specified using
Astop1. |
Ast2 | Attenuation in the second stopband (dB), specified using
Astop2. |
BWp | Bandwidth of the filter passband, specified as
BWpass in normalized frequency
units. |
BWst | Frequency width between the two stopband frequencies,
specified as BWstop in normalized
frequency units. |
F3dB1 | Frequency of the 3 dB point below the passband value for the first cutoff, specified in normalized frequency units. Applies to IIR filters. |
F3dB2 | Frequency of the 3 dB point below the passband value for the second cutoff, specified in normalized frequency units. Applies to IIR filters. |
Fc1 | First cutoff frequency (normalized frequency units),
specified using Fcutoff1. Applies to
FIR filters. |
Fc2 | Second cutoff frequency (normalized frequency units),
specified using Fcutoff1. Applies to
FIR filters. |
Fp1 | Frequency at the edge of the start of the passband,
specified as Fpass1 in normalized
frequency units. |
Fp2 | Frequency at the edge of the end of the passband,
specified as Fpass2 in normalized
frequency units. |
Fst1 | Frequency at the edge of the end of the first stop band,
specified as Fstop1 in normalized
frequency units. |
Fst2 | Frequency at the edge of the start of the second stop
band, specified as Fstop2 in normalized
frequency units. |
N | Filter order for FIR filters. Or both the numerator and
denominator orders for IIR filters when
Na and Nb are not
provided. Specified using
FilterOrder. |
Nb | Numerator order for IIR filters, specified using the
NumOrder property. |
Na | Denominator order for IIR filters, specified using the
DenOrder property. |
C | Constrained band flag. This enables you to specify passband ripple or stopband attenuation for fixed-order designs in one or two of the three bands. For more details, see |
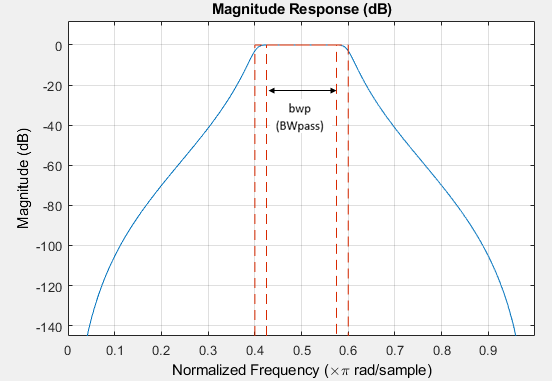
Graphically, the filter specifications look similar to those shown in this figure.
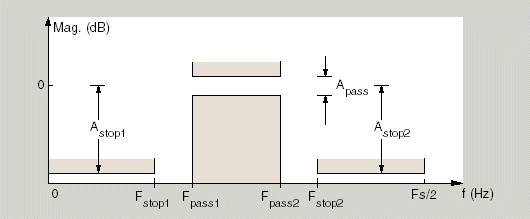
Regions between specification values like Fst1 and
Fp1 are transition regions where the filter response
is not explicitly defined.
The design methods available for designing the filter depend on the
specification expression. You can obtain these methods using the designmethods function. This
table lists each specification expression supported by
fdesign.bandpass and the available corresponding
design methods.
| Specification expression | Supported design methods |
|---|---|
'Fst1,Fp1,Fp2,Fst2,Ast1,Ap,Ast2' | butter, cheby1,
cheby2, ellip,
equiripple,
kaiserwin |
'N,F3dB1,F3dB2' | butter |
'N,F3dB1,F3dB2,Ap' | cheby1 |
'N,F3dB1,F3dB2,Ast' | cheby2,
ellip |
'N,F3dB1,F3dB2,Ast1,Ap,Ast2' | ellip |
'N,F3dB1,F3dB2,BWp' | cheby1 |
'N,F3dB1,F3dB2,BWst' | cheby2 |
'N,Fc1,Fc2' | window |
'N,Fc1,Fc2,Ast1,Ap,Ast2' | fircls |
'N,Fp1,Fp2,Ap' | cheby1 |
'N,Fp1,Fp2,Ast1,Ap,Ast2' | ellip |
'N,Fst1,Fp1,Fp2,Fst2' | iirlpnorm,
equiripple,
firls |
'N,Fst1,Fp1,Fp2,Fst2,C' | equiripple |
'N,Fst1,Fp1,Fp2,Fst2,Ap' | ellip |
'N,Fst1,Fst2,Ast' | cheby2 |
'Nb,Na,Fst1,Fp1,Fp2,Fst2' | iirlpnorm |
To design the filter, call the design function with one of
these design methods as an input. You can choose the type of filter response
by passing 'FIR' or 'IIR' to the
design function. For more details, see design. Enter
help(bandpassSpecs,'method') at the MATLAB® command line to obtain detailed help on the design options for
a given design method.
value1,...,valueN — Specification values
comma-separated list of values
Specification values, specified as a comma-separated list of values.
Specify a value for each option in spec in the same
order that the options appear in the expression.
Example: bandpassSpecs =
fdesign.bandpass('N,Fc1,Fc2,Ast1,Ap,Ast2',n,fc1,fc2,ast1,ap,ast2)
The input arguments below provide more details for each option in the expression.
n — Filter order
positive integer
Filter order for FIR filters, specified as a positive integer.
In the case of an IIR filter design, if nb
and na are not provided, this value is
interpreted as both the numerator order and the denominator
order.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
nb — Numerator order for IIR filters
nonnegative integer
Numerator order for IIR filters, specified as a nonnegative integer.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
na — Denominator order for IIR filters
positive integer
Denominator order for IIR filters, specified as a positive integer.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
c — Constrained band flag
logical
This enables you to specify passband ripple or stopband attenuation for fixed-order designs in one or two of the three bands.
In the specification
'N,Fst1,Fp1,Fp2,Fst2,C', you cannot
specify constraints for all three bands (two stopbands and one
passband) simultaneously. You can specify constraints in any one
or two bands.
Consider the following bandpass design specification where both the stopbands are constrained to the default value 60 dB.
Example: spec =
fdesign.bandpass('N,Fst1,Fp1,Fp2,Fst2,C',100,800,1e3,1.4e3,1.6e3,1e4);
spec.Stopband1Constrained=true;
spec.Stopband2Constrained=true;
ap — Passband ripple
positive scalar
Passband ripple, specified as a positive scalar in dB. If
magunits is 'linear'
or 'squared', the passband ripple is
converted and stored in dB by the function regardless of how it
has been specified.
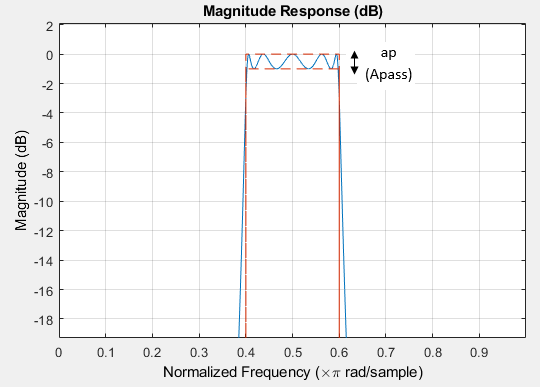
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
ast — Stopband attenuation
positive scalar
Stopband attenuation, specified as a positive scalar in dB. If
magunits is 'linear'
or 'squared', the stopband attenuation is
converted and stored in dB by the function regardless of how it
has been specified.
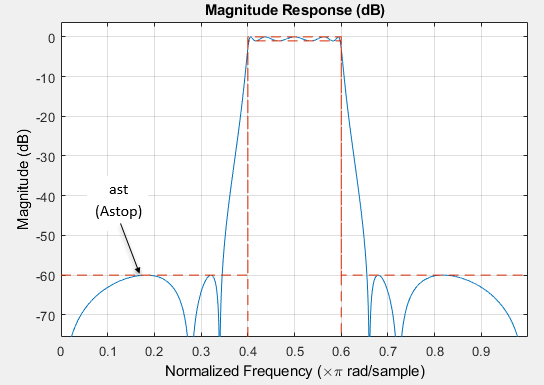
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
ast1 — First stopband attenuation
positive scalar
Attenuation in the first stopband, specified as a positive
scalar in dB. If magunits is
'linear' or 'squared',
the first stopband attenuation is converted and stored in dB by
the function regardless of how it has been specified.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
ast2 — Second stopband attenuation
positive scalar
Attenuation in the second stopband, specified as a positive
scalar in dB. If magunits is
'linear' or 'squared',
the second stopband attenuation is converted and stored in dB by
the function regardless of how it has been specified.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
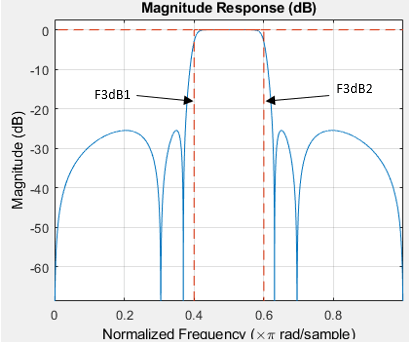
F3dB1 — First 3 dB frequency
positive scalar
First 3 dB frequency, specified as positive scalar in normalized frequency units.
This is the frequency of the 3 dB point below the passband value for the first cutoff. This input argument applies to IIR filters only.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
F3dB2 — Second 3 dB frequency
positive scalar
Second 3 dB frequency, specified as positive scalar in normalized frequency units.
This is the frequency of the 3 dB point below the passband value for the second cutoff. This input argument applies to IIR filters only.

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
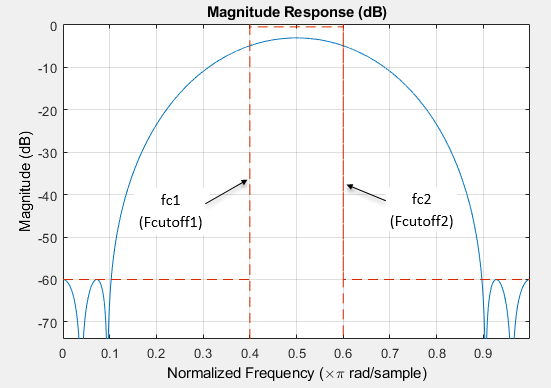
fc1 — First cutoff frequency
positive scalar
First cutoff frequency, specified as positive scalar in normalized frequency units.
This input argument applies to FIR filters only.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
fc2 — Second cutoff frequency
positive scalar
Second cutoff frequency, specified as positive scalar in normalized frequency units.
This input argument applies to FIR filters only.

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
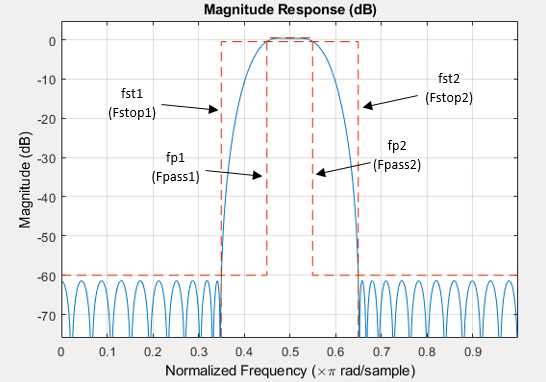
fst1 — First stopband frequency
positive scalar
First stopband frequency, specified as positive scalar in normalized frequency units.
This is the frequency at the edge of the end of the first stopband.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
fst2 — Second stopband frequency
positive scalar
Second stopband frequency, specified as a positive scalar in normalized frequency units.
This is the frequency at the edge of the start of the second stopband.

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
fp1 — First passband frequency
positive scalar
First passband frequency, specified as positive scalar in normalized frequency units.
This is the frequency at the edge of the start of the first passband.

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
fp2 — Second passband frequency
positive scalar
Second passband frequency, specified as positive scalar in normalized frequency units.
This is the frequency at the edge of the end of the passband.

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
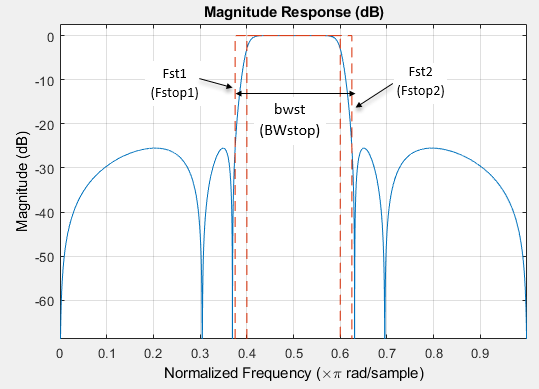
bwst — Frequency width between stopband frequencies
positive scalar
Frequency width between the two stopband frequencies, specified as a positive scalar in normalized frequency units.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Fs — Sample rate
scalar
Sample rate of the signal to be filtered, specified as a scalar in Hz.
Specify the sample rate as a scalar trailing the other numerical values
provided. When Fs is provided, Fs
is assumed to be in Hz, as are all other frequency values. Note that you do
not have to change the specification string.
The following design has the specification string set to
'Fst1,Fp1,Fp2,Fst2,Ast1,Ap,Ast2', and sample rate set
to 8000 Hz.
bandpassSpecs =
fdesign.bandpass('Fst1,Fp1,Fp2,Fst2,Ast1,Ap,Ast2',1600,2000,2400,2800,60,1,80,8000);
filt = design(bandpassSpecs,'Systemobject',true);
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
magunits — Magnitude units
'dB' (default) | 'linear' | 'squared'
Magnitude specification units, specified as 'dB',
'linear', or 'squared'. If this
argument is omitted, the object assumes the units of magnitude to be
'dB'. Note that the magnitude specifications are
always converted and stored in dB regardless of how they were specified. If
Fs is one of the input arguments,
magunits must be specified after
Fs in the input argument list.
Output Arguments
bandpassSpecs — Bandpass filter design specification object
bandpass
bandpassBandpass filter design specification object, returned as a
bandpass object. The fields of the object depend on the
spec input character vector.
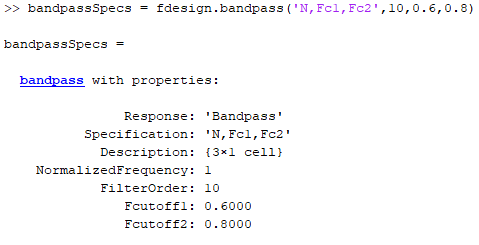
Consider an example where the spec argument is set to
'N,Fc1,Fc2', and the corresponding values are set to
10, 0.6, and
0.8, respectively. The bandpass
filter design specification object is populated with the following fields:
Version History
Introduced in R2009a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)