fdesign.pulseshaping
(Removed) Pulse-shaping filter specification object
The fdesign.pulseshaping filter specification object has been
removed. Use rcosdesign or gaussdesign instead. For more information on how to update your existing
code, see Compatibility Considerations.
Syntax
D = fdesign.pulseshaping
D = fdesign.pulseshaping(sps)
D = fdesign.pulseshaping(sps,shape)
d = fdesign.pulseshaping(sps,shape,spec,value1,value2,...)
d = fdesign.pulseshaping(...,fs)
d = fdesign.pulseshaping(...,magunits)
Description
D = fdesign.pulseshaping constructs a specification object
D, which can be used to design a minimum-order raised cosine
filter object with a default stop band attenuation of 60 dB and a rolloff factor of
0.25.
D = fdesign.pulseshaping(sps) constructs a minimum-order raised
cosine filter specification object d with a positive integer-valued
oversampling factor, SamplesPerSymbol.
D = fdesign.pulseshaping(sps,shape) constructs
d where shape specifies the
PulseShape property. Valid entries for shape
are:
'Raised Cosine''Square Root Raised Cosine''Gaussian'
d = fdesign.pulseshaping(sps,shape,spec,value1,value2,...)
constructs d where spec defines the
Specification properties. The entries for
spec specify various properties of the filter, including the
order and frequency response. Valid entries for spec depend upon the
shape property. For 'Raised Cosine' and
'Square Root Raised Cosine' filters, the valid entries for
spec are:
'Ast,Beta'(minimum order; default)'Nsym,Beta''N,Beta'
The filter specifications are defined as follows:
Ast—stopband attenuation (in dB). The default stopband attenuation for a raised cosine filter is 60 dB. The default stopband attenuation for a square root raised cosine filter is 30 dB. IfAstis specified, the minimum-order filter is returned.Beta—rolloff factor expressed as a real-valued scalar ranging from 0 to 1. Smaller rolloff factors result in steeper transitions between the passband and stopband of the filter.Nsym—filter order in symbols. The length of the impulse response is given byNsym*SamplesPerSymbol+1. The productNsym*SamplesPerSymbolmust be even.N—filter order (must be even). The length of the impulse response isN+1.
If the shape property is specified as
'Gaussian', the valid entries for spec are:
'Nsym,BT'(default)
The filter specifications are defined as follows:
Nsym—filter order in symbols.Nsymdefaults to 6. The length of the filter impulse response isNsym*SamplesPerSymbol+1. The productNsym*SamplesPerSymbolmust be even.BT—the 3 dB bandwidth-symbol time product.BTis a positive real-valued scalar, which defaults to 0.3. Larger values ofBTproduce a narrower pulse width in time with poorer concentration of energy in the frequency domain.
d = fdesign.pulseshaping(...,fs) specifies the
sampling frequency of the signal to be filtered. fs must be specified
as a scalar trailing the other numerical values provided. For this case,
fs is assumed to be in Hz and is used for analysis and
visualization.
d = fdesign.pulseshaping(...,magunits)
specifies the units for any magnitude specification you provide in the input arguments.
Valid entries for magunits are:
linear— specify the magnitude in linear unitsdB— specify the magnitude in dB (decibels)squared— specify the magnitude in power units
When you omit the magunits argument, fdesign
assumes that all magnitudes are in decibels. Note that fdesign stores
all magnitude specifications in decibels (converting to decibels when necessary)
regardless of how you specify the magnitudes.
After creating the specification object d, you can use the
design function to create a filter object
such as h in the following
example:
d = fdesign.pulseshaping(8,'Raised Cosine','Nsym,Beta',6,0.25); h = design(d);
Normally, the Specification property of the specification object
also determines which design methods you can use when you create the filter object.
Currently, regardless of the Specification property, the
design function uses the window design method
with all fdesign.pulseshaping specification objects. The
window method creates an FIR filter with a windowed impulse
response.
Examples
Pulse-shaping can be used to change the waveform of transmitted pulses so the signal bandwidth matches that of the communication channel. This helps to reduce distortion and intersymbol interference (ISI).
This example shows how to design a minimum-order raised cosine filter that provides a stop band attenuation of 60 dB, rolloff factor of 0.50, and 8 samples per symbol.
h = fdesign.pulseshaping(8,'Raised Cosine','Ast,Beta',60,0.50);
Hd = design(h);
fvtool(Hd)
This code generates the following figure.

This example shows how to design a raised cosine filter that spans 8 symbol durations (i.e., of order 8 symbols), has a rolloff factor of 0.50, and oversampling factor of 10.
h = fdesign.pulseshaping(10,'Raised Cosine','Nsym,Beta',8,0.50);
Hd = design(h);
fvtool(Hd, 'impulse')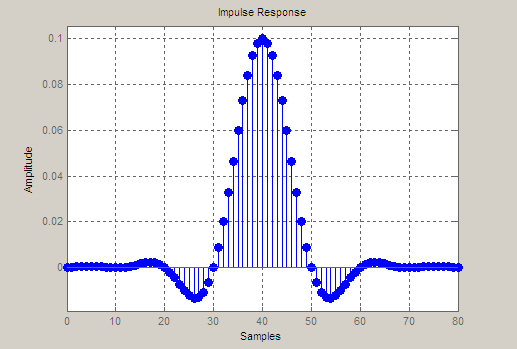
This example shows how to design a square root raised cosine filter of order 42, rolloff factor of 0.25, and 10 samples per symbol.
h = fdesign.pulseshaping(10,'Square Root Raised Cosine','N,Beta',42);
Hd = design(h);
fvtool(Hd, 'impulse')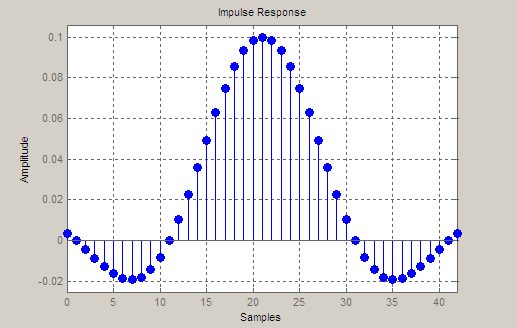
The following example demonstrates how to create a Gaussian pulse-shaping filter with an oversampling factor (sps) of 10, a bandwidth-time symbol product of 0.2, and 8 symbol periods. The sampling frequency is specified as 10 kHz.

