filter
1-D digital filter
Description
y = filter(b,a,x)x using a rational transfer function defined
by the numerator and denominator coefficients b and a.
If a(1) is not equal to 1,
then filter normalizes the filter coefficients
by a(1). Therefore, a(1) must
be nonzero.
If
xis a vector, thenfilterreturns the filtered data as a vector of the same size asx.If
xis a matrix, thenfilteracts along the first dimension and returns the filtered data for each column.If
xis a multidimensional array, thenfilteracts along the first array dimension whose size does not equal 1.
Examples
Moving-Average Filter
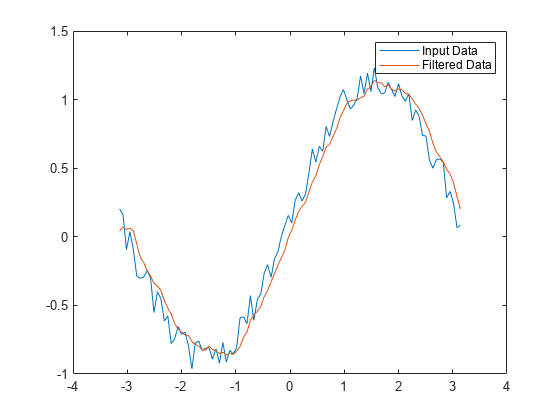
A moving-average filter is a common method used for smoothing noisy data. This example uses the filter function to compute averages along a vector of data.
Create a 1-by-100 row vector of sinusoidal data that is corrupted by random noise.
t = linspace(-pi,pi,100); rng default %initialize random number generator x = sin(t) + 0.25*rand(size(t));
A moving-average filter slides a window of length along the data, computing averages of the data contained in each window. The following difference equation defines a moving-average filter of a vector :
For a window size of 5, compute the numerator and denominator coefficients for the rational transfer function.
windowSize = 5; b = (1/windowSize)*ones(1,windowSize); a = 1;
Find the moving average of the data and plot it against the original data.
y = filter(b,a,x); plot(t,x) hold on plot(t,y) legend('Input Data','Filtered Data')
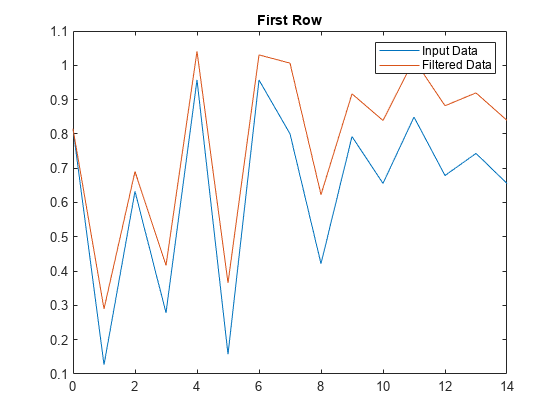
Filter Matrix Rows
This example filters a matrix of data with the following rational transfer function.
Create a 2-by-15 matrix of random input data.
rng default %initialize random number generator x = rand(2,15);
Define the numerator and denominator coefficients for the rational transfer function.
b = 1; a = [1 -0.2];
Apply the transfer function along the second dimension of x and return the 1-D digital filter of each row. Plot the first row of original data against the filtered data.
y = filter(b,a,x,[],2); t = 0:length(x)-1; %index vector plot(t,x(1,:)) hold on plot(t,y(1,:)) legend('Input Data','Filtered Data') title('First Row')
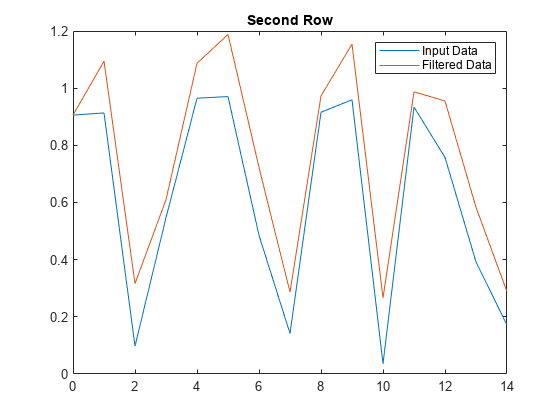
Plot the second row of input data against the filtered data.
figure plot(t,x(2,:)) hold on plot(t,y(2,:)) legend('Input Data','Filtered Data') title('Second Row')
Specify Initial Conditions
Define a moving-average filter with a window size of 3.
windowSize = 3; b = (1/windowSize)*ones(1,windowSize); a = 1;
Find the 3-point moving average of a 1-by-6 row vector of data.
x = [2 1 6 2 4 3]; y = filter(b,a,x)
y = 1×6
0.6667 1.0000 3.0000 3.0000 4.0000 3.0000
By default, the filter function initializes the filter delays as zero, assuming that both past inputs and outputs are zero. In this case, the first two elements of y are the 3-point moving average of the first element and the first two elements of x, respectively. In other words, the first element 0.6667 is the 3-point average of 2, and the second element 1 is the 3-point average of 2 and 1.
To include additional past inputs and outputs in your data, specify the initial conditions as the filter delays. These initial conditions for the present inputs are the final conditions that are obtained from applying the same transfer function to the past inputs (and past outputs). For example, include past inputs of [1 3]. Without filter delays, the past outputs are (0+0+1)/3 and (0+1+3)/3.
x_past = [1 3]; y_past = filter(b,a,x_past)
y_past = 1×2
0.3333 1.3333
However, you can continue applying the same transfer function to generate further nonzero outputs, assuming that the tails of these past inputs are zero. These further outputs are (1+3+0)/3 and (3+0+0)/3, which represent the final conditions obtained from the past inputs. To compute these final conditions, specify the second output argument of the filter function.
[y_past,zf] = filter(b,a,x_past)
y_past = 1×2
0.3333 1.3333
zf = 2×1
1.3333
1.0000
To include the past inputs in the present data, specify the filter delays by using the fourth input argument of the filter function. Use the final conditions from the past data as the initial conditions for the present data.
y = filter(b,a,x,zf)
y = 1×6
2.0000 2.0000 3.0000 3.0000 4.0000 3.0000
In this case, the first element of y becomes the 3-point moving average of 1, 3, and 2, which is 2, and the second element of y becomes the moving average of 3, 2, and 1, which is 2.
Filter Data in Sections
Use initial and final conditions for filter delays to filter data in sections, especially if memory limitations are a consideration.
Generate a large random data sequence and split it into two segments, x1 and x2.
x = randn(10000,1); x1 = x(1:5000); x2 = x(5001:end);
The whole sequence, x, is the vertical concatenation of x1 and x2.
Define the numerator and denominator coefficients for the rational transfer function,
b = [2,3]; a = [1,0.2];
Filter the subsequences x1 and x2 one at a time. Output the final conditions from filtering x1 to store the internal status of the filter at the end of the first segment.
[y1,zf] = filter(b,a,x1);
Use the final conditions from filtering x1 as initial conditions to filter the second segment, x2.
y2 = filter(b,a,x2,zf);
y1 is the filtered data from x1, and y2 is the filtered data from x2. The entire filtered sequence is the vertical concatenation of y1 and y2.
Filter the entire sequence simultaneously for comparison.
y = filter(b,a,x); isequal(y,[y1;y2])
ans = logical
1
Input Arguments
b — Numerator coefficients of rational transfer function
vector
Numerator coefficients of the rational transfer function, specified as a vector.
Data Types: double | single | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical
Complex Number Support: Yes
a — Denominator coefficients of rational transfer function
vector
Denominator coefficients of the rational transfer function, specified as a vector.
Data Types: double | single | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical
Complex Number Support: Yes
x — Input data
vector | matrix | multidimensional array
Input data, specified as a vector, matrix, or multidimensional array.
Data Types: double | single | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical
Complex Number Support: Yes
zi — Initial conditions for filter delays
[] (default) | vector | matrix | multidimensional array
Initial conditions for filter delays, specified as a vector, matrix, or multidimensional array.
If
ziis a vector, then its length must bemax(length(a),length(b))-1.If
ziis a matrix or multidimensional array, then the size of the leading dimension must bemax(length(a),length(b))-1. The size of each remaining dimension must match the size of the corresponding dimension ofx. For example, consider usingfilteralong the second dimension (dim = 2) of a 3-by-4-by-5 arrayx. The arrayzimust have size[max(length(a),length(b))-1]-by-3-by-5.
The default value, specified by [], initializes
all filter delays to zero.
Data Types: double | single | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical
Complex Number Support: Yes
dim — Dimension to operate along
positive integer scalar
Dimension to operate along, specified as a positive integer scalar. If you do not specify the dimension, then the default is the first array dimension of size greater than 1.
Consider a two-dimensional input array, x.
If
dim = 1, thenfilter(b,a,x,zi,1)operates along the columns ofxand returns the filter applied to each column.
If
dim = 2, thenfilter(b,a,x,zi,2)operates along the rows ofxand returns the filter applied to each row.
If dim is greater than ndims(x), then
filter considers x as if it has
additional dimensions up to dim with sizes of 1. For
example, if x is a matrix with a size of 2-by-3 and
dim = 3, then filter operates
along the third dimension of x as if it has the size of
2-by-3-by-1.
Data Types: double | single | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical
Output Arguments
y — Filtered data
vector | matrix | multidimensional array
Filtered data, returned as a vector, matrix, or multidimensional
array of the same size as the input data, x.
If x is of type single,
then filter natively computes in single precision,
and y is also of type single.
Otherwise, y is returned as type double.
Data Types: double | single
zf — Final conditions for filter delays
vector | matrix | multidimensional array
Final conditions for filter delays, returned as a vector, matrix, or multidimensional array.
If
xis a vector, thenzfis a column vector of lengthmax(length(a),length(b))-1.If
xis a matrix or multidimensional array, thenzfis an array of column vectors of lengthmax(length(a),length(b))-1, such that the number of columns inzfis equivalent to the number of columns inx. For example, consider usingfilteralong the second dimension (dim = 2) of a 3-by-4-by-5 arrayx. The arrayzfhas size[max(length(a),length(b))-1]-by-3-by-5.
Data Types: double | single
More About
Rational Transfer Function
The input-output description of the filter operation on a
vector in the Z-transform domain is a rational transfer function. A rational
transfer function is of the form
which handles both finite impulse response (FIR) and infinite impulse response (IIR) filters [1]. Here, X(z) is the Z-transform of the input signal x, Y(z) is the Z-transform of the output signal y, na is the feedback filter order, and nb is the feedforward filter order. Due to normalization, assume a(1) = 1.
For a discrete signal with L elements, you can also express the rational transfer function as the difference equation
Furthermore, you can represent the rational transfer function using its direct-form II
transposed implementation, as in the following diagram of an IIR digital filter. In
the diagram, na = nb =
n–1. If your feedback and feedforward filter orders are different, or na ≠
nb, then you can treat the higher-order terms as 0. For example, for
a filter with a = [1,2] and b = [2,3,2,4], you
can assume a = [1,2,0,0].

The operation of filter at a sample point m is given
by the time-domain difference equations
By default, the filter function initializes the filter delays
as zero, where wk(0) =
0. This initialization assumes both past inputs and outputs to be
zero. To include nonzero past inputs in the present data, specify the initial
conditions of the present data as the filter delays. You can consider the filter
delays to be the final conditions that are obtained from applying the same transfer
function to the past inputs (and past outputs). You can specify the fourth input
argument zi when using filter to set the
filter delays, where wk(0) =
zi(k). You can also specify the second output
argument zf when using filter to access the
final conditions, where wk(L)
= zf(k).
Tips
To use the
filterfunction with thebcoefficients from an FIR filter, usey = filter(b,1,x).If you have Signal Processing Toolbox™, use
y = filter(d,x)to filter an input signalxwith adigitalFilter(Signal Processing Toolbox) objectd. To generatedbased on frequency-response specifications, usedesignfilt(Signal Processing Toolbox).See Digital Filtering (Signal Processing Toolbox) for more on filtering functions.
References
[1] Oppenheim, Alan V., Ronald W. Schafer, and John R. Buck. Discrete-Time Signal Processing. Upper Saddle River, NJ: Prentice-Hall, 1999.
Extended Capabilities
Tall Arrays
Calculate with arrays that have more rows than fit in memory.
Usage notes and limitations:
The two-output syntax [y,zf] = filter(___) is not supported when dim > 1.
For more information, see Tall Arrays.
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
Usage notes and limitations:
If supplied,
dimmust be a constant.See Variable-Sizing Restrictions for Code Generation of Toolbox Functions (MATLAB Coder).
GPU Code Generation
Generate CUDA® code for NVIDIA® GPUs using GPU Coder™.
Usage notes and limitations:
If supplied,
dimmust be a constant.See Variable-Sizing Restrictions for Code Generation of Toolbox Functions (MATLAB Coder).
Thread-Based Environment
Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.
This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.
GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.
Usage notes:
y = filter(d,x)is supported fordigitalFilterobjectdandgpuArrayinputx. For IIR filters,digitalFilterobjects store filter coefficients as a matrix of second-order sections (SOS). For agpuArrayinput, it is not necessary to convert the SOS matrix to agpuArray.
For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Distributed Arrays
Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.
This function fully supports distributed arrays. For more information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox).
Version History
Introduced before R2006a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)