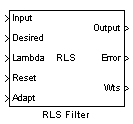
RLS Filter
Compute filtered output, filter error, and filter weights for given input and desired signal using RLS adaptive filter algorithm
Libraries:
DSP System Toolbox /
Filtering /
Adaptive Filters
Description
The RLS Filter block recursively computes the least squares estimate (RLS) of the FIR filter weights. The block estimates the filter weights (also known as the coefficients) needed to minimize the error e(n) between the output signal y(n) and the desired signal d(n). For more information, see Algorithms. For more information on adaptive filters, see Overview of Adaptive Filters and Applications.
Examples
Ports
Input
Output
Parameters
Block Characteristics
Data Types |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
Algorithms
The RLS filter is expressed in matrix form as
where λ−1 denotes the reciprocal of the exponential weighting factor.
The variables are as follows:
| Variable | Description |
|---|---|
n | The current time index |
u(n) | The vector of buffered input samples at step n |
P(n) | The inverse covariance matrix at step n |
k(n) | The gain vector at step n |
The vector of filter-tap estimates at step n | |
y(n) | The filtered output at step n |
e(n) | The estimation error at step n |
d(n) | The desired response at step n |
λ | The forgetting factor |
The implementation of the algorithm in the block is optimized by exploiting the symmetry of the inverse covariance matrix P(n). This decreases the total number of computations by a factor of two.
References
[1] Hayes, M.H. Statistical Digital Signal Processing and Modeling. New York: John Wiley & Sons, 1996.
Extended Capabilities
Version History
Introduced before R2006a