Variance
Variance of input or sequence of inputs
Libraries:
DSP System Toolbox /
Statistics
Description
The Variance block computes the unbiased variance of each row or column of the input, or along vectors of a specified dimension of the input. It can also compute the variance of the entire input. You can specify the dimension using the Find the variance value over parameter. The Variance block can also track the variance in a sequence of inputs over a period of time. To track the variance in a sequence of inputs, select the Running variance parameter.
Note
The Running mode in the Variance block will be removed in a future release. To compute the running variance in Simulink®, use the Moving Variance block instead.
Ports
Input
In — Data input
vector | matrix | N-D array
The block accepts real-valued or complex-valued multichannel and multidimensional inputs.
This port is unnamed until you select the Running
variance parameter and set the Reset
port parameter to any option other than
None.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | fixed point
Complex Number Support: Yes
Rst — Reset port
scalar
Specify the event that causes the block to reset the running variance. The sample time of the Rst input must be a positive integer multiple of the input sample time.
Dependencies
To enable this port, select the Running
variance parameter and set the Reset
port parameter to any option other than
None.
Data Types: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32 | Boolean
Output
Port_1 — Variance along the specified dimension
scalar | vector | matrix | N-D array
When you do not select the Running variance
parameter, the block computes the variance in each row or column of the
input, or along vectors of a specified dimension of the input. It can
also compute the variance of the entire input at each individual sample
time. Each element in the output array y is the
variance of the corresponding column, row, or entire input. The output
array y depends on the setting of the Find
the variance value over parameter.
Consider a three-dimensional input signal of size M-by-N-by-P. When you set Find the variance value over to:
Entire input— The output at each sample time is a scalar that contains the variance of the M-by-N-by-P input matrix.Each row— The output at each sample time consists of an M-by-1-by-P array, where each element contains the variance of each vector over the second dimension of the input. For an M-by-N matrix input, the output at each sample time is an M-by-1 column vector.Each column— The output at each sample time consists of a 1-by-N-by-P array, where each element contains the variance of each vector over the first dimension of the input. For an M-by-N matrix input, the output at each sample time is a 1-by-N row vector.In this mode, the block treats length-M unoriented vector inputs as M-by-1 column vectors.
Specified dimension— The output at each sample time depends on the value of the Dimension parameter. If you set the Dimension to1, the output is the same as when you selectEach column. If you set the Dimension to2, the output is the same as when you selectEach row. If you set the Dimension to3, the output at each sample time is an M-by-N matrix containing the variance of each vector over the third dimension of the input.
When you select Running variance, the block tracks the variance of each channel in a time sequence of inputs. In this mode, you must also specify a value for the Input processing parameter. When you set Input processing to:
Elements as channels (sample based)— The block treats each element of the input as a separate channel. For a three-dimensional input signal of size M-by-N-by-P, the block outputs an M-by-N-by-P array. Each element yijk of the output contains the variance of the element uijk for all inputs since the last reset.When a reset event occurs, the running variance yijk in the current frame is reset to the element uijk.
Columns as channels (frame based)— The block treats each column of the input as a separate channel. This option does not support input signals with more than two dimensions. For a two-dimensional input signal of size M-by-N, the block outputs an M-by-N matrix. Each element yij of the output contains the variance of the elements in the jth column of all inputs since the last reset, up to and including the element uij of the current input.When a reset event occurs, the running variance for each channel becomes the variance of all the samples in the current input frame, up to and including the current input sample.
The data type of the output matches the data type of the input.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | fixed point
Parameters
Main Tab
Running variance — Option to select running variance
off (default) | on
When you select the Running variance parameter, the block tracks the variance value of each channel in a time sequence of inputs.
Find the variance value over — Dimension over which variance is computed
Each column (default) | Entire input | Each row | Specified dimension
Each column— The block outputs the variance over each column.Each row— The block outputs the variance over each row.Entire input— The block outputs the variance over the entire input.Specified dimension— The block outputs the variance over the dimension specified in the Dimension parameter.
Dependencies
To enable this parameter, clear the Running variance parameter.
Dimension — Custom dimension
1 (default) | scalar
Specify the dimension (one-based value) of the input signal over which the variance is computed. The value of this parameter must be greater than 0 and less than or equal to the number of dimensions in the input signal.
Dependencies
To enable this parameter, set Find the variance value
over to Specified
dimension.
Input processing — Method to process the input in running mode
Columns as channels (frame
based) (default) | Elements as channels (sample
based)
Columns as channels (frame based)— The block treats each column of the input as a separate channel. This option does not support input signals with more than two dimensions. For a two-dimensional input signal of size M-by-N, the block outputs an M-by-N matrix. Each element yij of the output contains the variance of the elements in the jth column of all inputs since the last reset, up to and including the element uij of the current input.When a reset event occurs, the running variance for each channel becomes the variance of all the samples in the current input frame, up to and including the current input sample.
Elements as channels (sample based)— The block treats each element of the input as a separate channel. For a three-dimensional input signal of size M-by-N-by-P, the block outputs an M-by-N-by-P array. Each element yijk of the output contains the variance of the element uijk for all inputs since the last reset.When a reset event occurs, the running variance yijk in the current frame is reset to the element uijk.
Variable-Size Inputs
When your inputs are of variable size, and you select the Running variance parameter, then:
If you set the Input processing parameter to
Elements as channels (sample based), the state is reset.If you set the Input processing parameter to
Columns as channels (frame based), then:When the input size difference is in the number of channels (number of columns), the state is reset.
When the input size difference is in the length of channels (number of rows), the state is not reset, and the running operation is carried out as usual.
Dependencies
To enable this parameter, select the Running variance parameter.
Reset port — Reset event
None (default) | Rising edge | Falling edge | Either edge | Non-zero sample
The block resets the running variance whenever a reset event is detected at the optional Rst port. The reset sample time must be a positive integer multiple of the input sample time.
When a reset event occurs while the Input
processing parameter is set to Elements as
channels (sample based), the running variance for each
channel is initialized to the value in the corresponding channel of the
current input. Similarly, when the Input processing
parameter is set to Columns as channels (frame
based), the running variance for each channel becomes
the variance of all the samples in the current input frame, up to and
including the current input sample.
Use this parameter to specify the reset event.
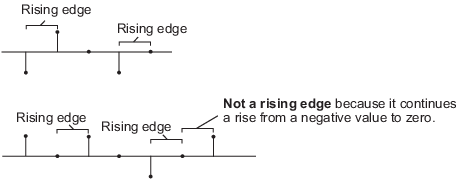
None— Disables the Rst port.Rising edge— Triggers a reset operation when the Rst input does one of the following:Rises from a negative value to either a positive value or zero.
Rises from zero to a positive value, where the rise is not a continuation of a rise from a negative value to zero.
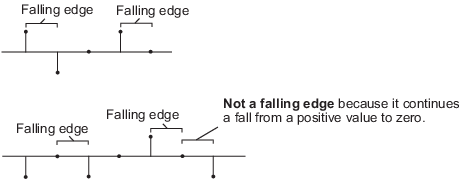
Falling edge— Triggers a reset operation when the Rst input does one of the following:Falls from a positive value to a negative value or zero.
Falls from zero to a negative value, where the fall is not a continuation of a fall from a positive value to zero.
Either edge— Triggers a reset operation when the Rst input is aRising edgeorFalling edge.Non-zero sample— Triggers a reset operation at each sample time, when the Rst input is not zero.
Note
When running simulations in the Simulink multitasking mode, reset signals have a one-sample latency. Therefore, when the block detects a reset event, there is a one-sample delay at the reset port rate before the block applies the reset. For more information on latency and the Simulink tasking modes, see Excess Algorithmic Delay (Tasking Latency) and Time-Based Scheduling and Code Generation (Simulink Coder).
Dependencies
To enable this parameter, select the Running variance parameter.
Data Types Tab
Note
To use these parameters, the data input must be fixed point. For all other inputs, the parameters on the Data Types tab are ignored.
Rounding mode — Method of rounding operation
Floor (default) | Ceiling | Convergent | Nearest | Round | Simplest | Zero
Specify the rounding mode for fixed-point operations. For more details, see rounding mode.
Saturate on integer overflow — Method of overflow action
off (default) | on
When you select this parameter, the block saturates the result of its
fixed-point operation. When you clear this parameter, the block wraps
the result of its fixed-point operation. For details on
saturate and wrap, see overflow
mode for fixed-point operations.
Input-squared product output — Data type of the input-squared term
Same as input (default) | Binary point scaling
The squares of the input elements are stored in the Input-squared product output data type. If the input is complex, the squares of the real and imaginary parts of the input are stored in this data type. For more details, see Fixed-Point Data Types.
You can set this parameter to:
Inherit: Same as input— The data type is same as the input data type.Binary point scaling— The Input-squared product output data type uses binary point scaling. If you select this option, the block displays the fields to specify the Word length and Fraction length. The Signedness is inherited from the input.
Input-sum-squared product — Data type of the input-sum-squared term
Same as input-squared
product (default) | Binary point scaling
The squares of the sum of the input elements are stored in the Input-sum-squared product data type. If the input is complex, the squares of the sum of the real parts and the squares of the sum of the imaginary parts are stored in this data type. For more details, see Fixed-Point Data Types.
You can set this parameter to:
Same as input-squared product— The data type is the same as the input squared-product data type.Binary point scaling— The Input-sum-squared product data type uses binary point scaling. If you select this option, the block displays the fields to specify the Word length and Fraction length. The Signedness is inherited from the input.
Accumulator — Accumulator data type
Same as input-squared
product (default) | Same as input | Binary point scaling
Accumulator specifies the data type of the output of an accumulation operation in the Variance block. See Fixed-Point Data Types for illustrations depicting the use of the accumulator data type in this block.
You can set this parameter to:
Same as input-squared product— The accumulator data type is the same as the input-squared product data type.Same as input— The accumulator data type is the same as the input data type.Binary point scaling— The Accumulator data type uses binary point scaling. If you select this option, the block displays the fields to specify the Word length and Fraction length. The Signedness is inherited from the input.
Output — Output data type
Same as input-squared
product (default) | Same as accumulator | Same as input | Binary point scaling
Output specifies the data type of the output of the Variance block. See Fixed-Point Data Types for information about the use of the output data type in this block. You can set it to:
Same as input-squared product— The output data type is the same as the input-squared product data type.Same as accumulator— The output data type is the same as the accumulator data type.Same as input— The output data type is the same as the input data type.Binary point scaling— The Output data type uses binary point scaling. If you select this option, the block displays the fields to specify the Word length and Fraction length. The Signedness is inherited from the input.
Lock data type settings against changes by the fixed-point tools — Prevent fixed-point tools from overriding data types
off (default) | on
Select this parameter to prevent the fixed-point tools from overriding the data types you specify on the block.
Block Characteristics
Data Types |
|
Direct Feedthrough |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
Zero-Crossing Detection |
|
More About
Variance
The variance of a discrete-time signal is the square of the standard deviation of the signal. Variance gives a measure of deviation of the signal from its mean value.
For purely real or imaginary input, u, of size M-by-N, the variance is given by:
where,
uij is the input data element at indices i, j.
M is the length of the jth column.
N is the number of columns.
For complex inputs, the variance is given by the following equation:
where,
σRe2 is the variance of the real part of the complex input.
σIm2 is the variance of the imaginary part of the complex input.
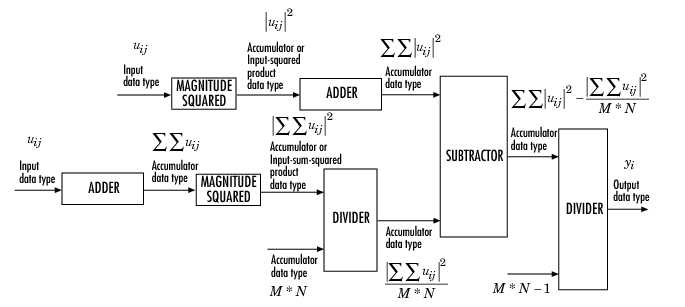
Fixed-Point Data Types
The following diagram shows the data types used within the Variance block when the input is fixed-point.
For complex inputs, the variance is given by the following equation:
Algorithms
Variance
When you clear the Running variance parameter in the block
and specify a dimension, the block produces results identical to the MATLAB®
var function when it is called as y =
var(u,0,D), where,
uis the data input.Dis the dimension.yis the variance along the specified dimension.
When this block calculates the variance along the entire input, the result is
identical to calling the var function as y =
var(u(:)).
For a complex input signal, the variance is the sum of the variances of the real and imaginary parts.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
Version History
Introduced before R2006a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)