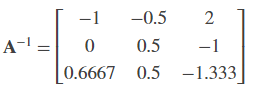Linear Algebra and Least Squares
Linear Algebra Blocks
The Matrices and Linear Algebra library provides three large sublibraries containing blocks for linear algebra; Linear System Solvers, Matrix Factorizations, and Matrix Inverses. A fourth library, Matrix Operations, provides other essential blocks for working with matrices.
Linear System Solvers
The Linear System Solvers library provides the following blocks for solving the system of linear equations AX = B:
Some of the blocks offer particular strengths for certain classes of problems. For example, the Cholesky Solver block is adapted for a square Hermitian positive definite matrix A, whereas the Backward Substitution block is suited for an upper triangular matrix A.
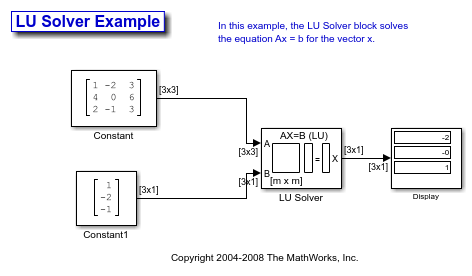
Solve AX=B Using the LU Solver Block
Open the ex_lusolver_tut model. The LU Solver block solves the equation Ax = b, where
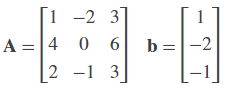
and finds x to be the vector [-2 0 1]'.
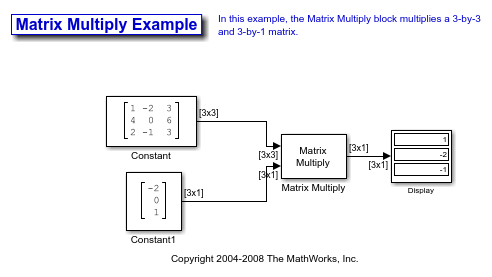
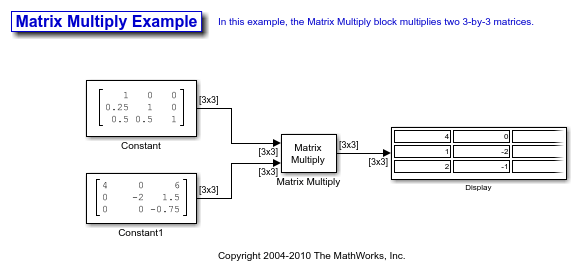
You can verify the solution by using the Matrix Multiply block to perform the multiplication Ax, as shown in the following ex_matrixmultiply_tut1 model.
Matrix Factorizations
The Matrix Factorizations library provides the following blocks for factoring various kinds of matrices:
Some of the blocks offer particular strengths for certain classes of problems. For example, the Cholesky Factorization block is suited to factoring a Hermitian positive definite matrix into triangular components, whereas the QR Factorization is suited to factoring a rectangular matrix into unitary and upper triangular components.
Factor a Matrix into Upper and Lower Submatrices Using the LU Factorization Block
Open the ex_lufactorization_tut model. The LU Factorization block factors a matrix Ap into upper and lower triangular submatrices U and L, where Ap is row equivalent to input matrix A, where
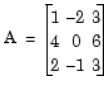
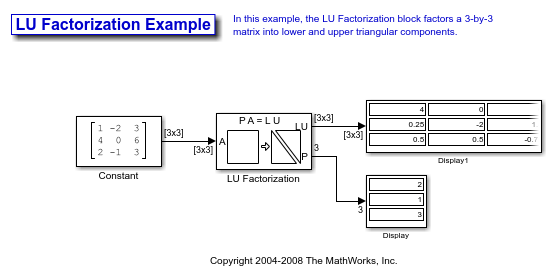
The lower output of the LU Factorization P is the permutation index vector, which indicates that the factored matrix Ap is generated from A by interchanging the first and second rows.
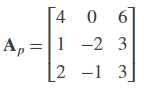
The upper output of the LU Factorization LU is a composite matrix containing the two submatrix factors U and L whose product LU is equal to Ap.
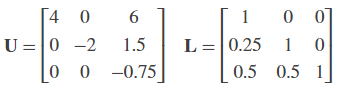
You can check that LU = Ap with the Matrix Multiply block, as shown in the following ex_matrixmultiply_tut2 model.
Matrix Inverses
The Matrix Inverses library provides the following blocks for inverting various kinds of matrices:
Find the Inverse of a Matrix Using the LU Inverse Block
Open the ex_luinverse_tut model. The LU Inverse block computes the inverse of input matrix A, where
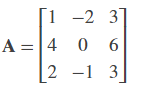
and then forms the product inv(A)*A, which yields the identity matrix of order 3, as expected.
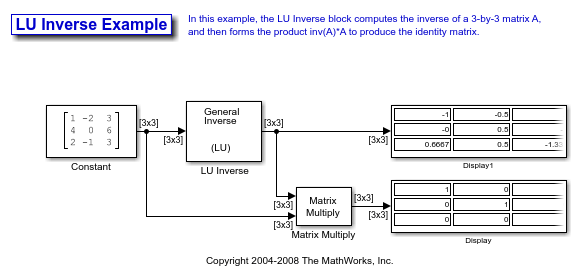
As shown above, the computed inverse is