Specify Fixed-Point Attributes for Blocks
Fixed-Point Block Parameters
Toolbox blocks that have fixed-point support usually allow you to specify fixed-point characteristics through block parameters. By specifying data type and scaling information for these fixed-point parameters, you can simulate your target hardware more closely.
Note
Floating-point inheritance takes precedence over the settings discussed in this section. When the block has floating-point input, all block data types match the input.
You can find most fixed-point parameters on the Data Types pane of toolbox blocks. The following figure shows a typical Data Types pane.

All toolbox blocks with fixed-point capabilities share a set of common parameters, but each block can have a different subset of these fixed-point parameters. The following table provides an overview of the most common fixed-point block parameters.
| Fixed-Point Data Type Parameter | Description |
|---|---|
Rounding Mode | Specifies the rounding mode for the block to use when the specified data type and scaling cannot exactly represent the result of a fixed-point calculation. See Rounding Modes for more information on the available options. |
Saturate on integer overflow | When you select this parameter, the block saturates the result of its fixed-point operation. When you clear this parameter, the block wraps the result of its fixed-point operation. For details on saturate and wrap, see Overflow Handling for fixed-point operations. |
Intermediate Product | Specifies the data type and scaling of the intermediate product for fixed-point blocks. Blocks that feed multiplication results back to the input of the multiplier use the intermediate product data type. See the reference page of a specific block to learn about the intermediate product data type for that block. |
Product Output | Specifies the data type and scaling of the product output for fixed-point blocks that must compute multiplication results. See the reference page of a specific block to learn about the product output data type for that block. For or complex-complex multiplication, the multiplication result is in the accumulator data type. See Multiplication Data Types for more information on complex fixed-point multiplication in toolbox software. |
Accumulator | Specifies the data type and scaling of the accumulator (sum) for fixed-point blocks that must hold summation results for further calculation. Most such blocks cast to the accumulator data type before performing the add operations (summation). See the reference page of a specific block for details on the accumulator data type of that block. |
Output | Specifies the output data type and scaling for blocks. |
Using the Data Type Assistant
The Data Type Assistant is an interactive graphical tool available on the Data Types pane of some Fixed-Point Designer™ blocks.
To learn more about using the Data Type Assistant to help you specify block data type parameters, see Specify Data Types Using Data Type Assistant (Simulink).
Checking Signal Ranges
Some Fixed-Point Designer blocks have Minimum and Maximum parameters on the Data Types pane. When a fixed-point data type has these parameters, you can use them to specify appropriate minimum and maximum values for range checking purposes.
To learn how to specify signal ranges and enable signal range checking, see Specify Signal Ranges (Simulink).
Specify System-Level Settings
You can monitor and control fixed-point settings for Fixed-Point Designer blocks at a system or subsystem level with the Fixed-Point Tool. For more information, see Fixed-Point Tool (Fixed-Point Designer).
Logging
The Fixed-Point Tool logs overflows, saturations, and simulation minimums and
maximums for Fixed-Point Designer blocks. The Fixed-Point Tool does not log overflows and saturations
when the Data overflow line in the Diagnostics >
Data Integrity pane of the Configuration Parameters dialog box is
set to None.
Autoscaling
You can use the Fixed-Point Tool autoscaling feature to set the scaling for toolbox fixed-point data types.
Data type override
toolbox blocks obey the Use local settings,
Double, Single, and
Off modes of the Data type
override parameter in the Fixed-Point Tool. The
Scaled double mode is also supported for
toolboxes source and byte-shuffling blocks, and for some arithmetic blocks such as
Difference and Normalization.
Scaled double is a double data type that retains fixed-point scaling information. Using the data type override, you can convert your fixed-point data types to scaled doubles. You can then simulate to determine the ideal floating-point behavior of your system. After you gather that information, you can turn data type override off to return to fixed-point data types, and your quantities still have their original scaling information because it was held in the scaled double data types.
Inherit via Internal Rule
Selecting appropriate word lengths and scalings for the fixed-point parameters in your
model can be challenging. To aid you, an Inherit via internal
rule choice is often available for fixed-point block data type
parameters, such as the Accumulator and Product
output signals. The following sections describe how the word and fraction
lengths are selected for you when you choose Inherit via internal
rule for a fixed-point block data type parameter in toolbox
software:
Note
In the equations in the following sections, WL = word length and FL = fraction length.
Internal Rule for Accumulator Data Types
The internal rule for accumulator data types first calculates the ideal, full-precision result. Where N is the number of addends:
For example, consider summing all the elements of a vector of length 6 and data type sfix10_En8. The ideal, full-precision result has a word length of 13 and a fraction length of 8.
The accumulator can be real or complex. The preceding equations are used for both the real and imaginary parts of the accumulator. For any calculation, after the full-precision result is calculated, the final word and fraction lengths set by the internal rule are affected by your particular hardware. See The Effect of the Hardware Implementation Pane on the Internal Rule for more information.
Internal Rule for Product Data Types
The internal rule for product data types first calculates the ideal, full-precision result:
For example, multiplying together the elements of a real vector of length 2 and data type sfix10_En8. The ideal, full-precision result has a word length of 20 and a fraction length of 16.
For real-complex multiplication, the ideal word length and fraction length is used for both the complex and real portion of the result. For complex-complex multiplication, the ideal word length and fraction length is used for the partial products, and the internal rule for accumulator data types described above is used for the final sums. For any calculation, after the full-precision result is calculated, the final word and fraction lengths set by the internal rule are affected by your particular hardware. See The Effect of the Hardware Implementation Pane on the Internal Rule for more information.
Internal Rule for Output Data Types
A few toolbox blocks have an Inherit via internal rule
choice available for the block output. The internal rule used in these cases is
block-specific, and the equations are listed in the block reference page.
As with accumulator and product data types, the final output word and fraction lengths set by the internal rule are affected by your particular hardware, as described in The Effect of the Hardware Implementation Pane on the Internal Rule.
The Effect of the Hardware Implementation Pane on the Internal Rule
The internal rule selects word lengths and fraction lengths that are appropriate for your hardware. To get the best results using the internal rule, you must specify the type of hardware you are using on the Hardware Implementation pane of the Configuration Parameters dialog box. To open this dialog box, click Modeling > Model Settings in the Simulink® toolstrip.

ASIC/FPGA. On an ASIC/FPGA target, the ideal, full-precision word length and fraction length calculated by the internal rule are used. If the calculated ideal word length is larger than the largest allowed word length, you receive an error.
Other targets. For all targets other than ASIC/FPGA, the ideal, full-precision word length calculated by the internal rule is rounded up to the next available word length of the target. The calculated ideal fraction length is used, keeping the least-significant bits.
If the calculated ideal word length for a product data type is larger than the largest word length on the target, you receive an error. If the calculated ideal word length for an accumulator or output data type is larger than the largest word length on the target, the largest target word length is used.
The largest word length allowed for Simulink and toolbox software on any target is 128 bits.
Internal Rule Examples
The following sections show examples of how the internal rule interacts with the Hardware Implementation pane to calculate accumulator data types and product data types.
Accumulator Data Types
Open the ex_internalRule_accumExp model.
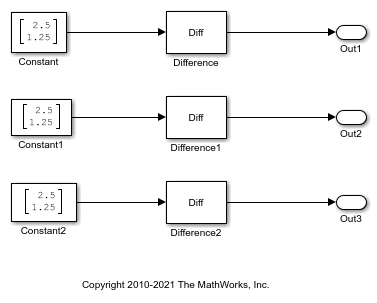
In the Difference blocks, the Accumulator parameter is set to Inherit: Inherit via internal rule, and the Output parameter is set to Inherit: Same as accumulator. Therefore, you can see the accumulator data type calculated by the internal rule on the output signal in the model.
In the preceding model, the Device type parameter in the Hardware Implementation pane of the Configuration Parameters dialog box is set to ASIC/FPGA. Therefore, the accumulator data type used by the internal rule is the ideal, full-precision result.
Calculate the full-precision word length for each of the Difference blocks in the model.

Calculate the full-precision fraction length, which is the same for each Matrix Sum block in this example:
Now change the Device type parameter in the Hardware Implementation pane of the Configuration Parameters dialog box to 32-bit Embedded Processor, by changing the parameters as shown in the following figure.
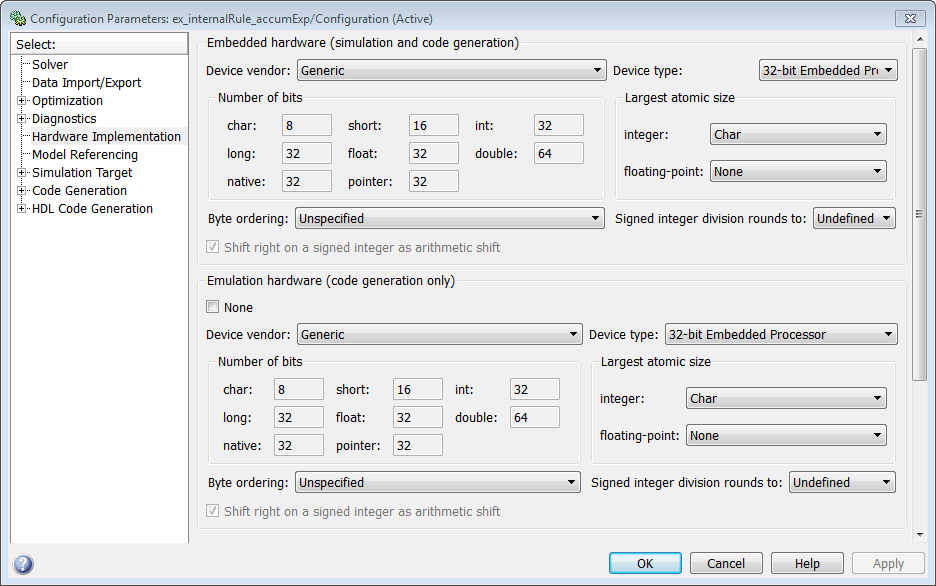
As you can see in the dialog box, this device has 8-, 16-, and 32-bit word lengths available. Therefore, the ideal word lengths of 10, 17, and 128 bits calculated by the internal rule cannot be used. Instead, the internal rule uses the next largest available word length in each case. You can see this if you rerun the model, as shown in the following figure.
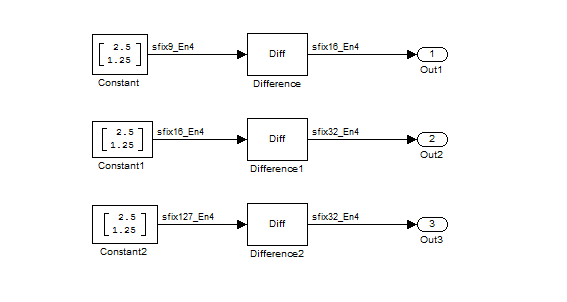
Product Data Types
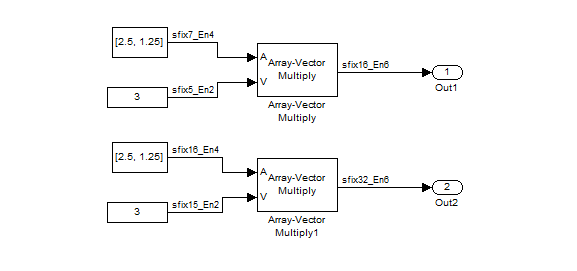
Open the ex_internalRule_prodExp model.
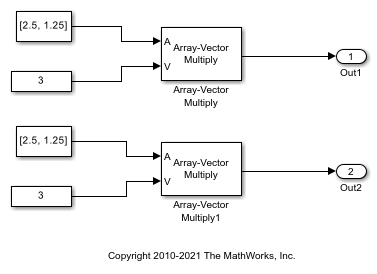
In the Array-Vector Multiply blocks, the Product Output parameter is set to Inherit: Inherit via internal rule, and the Output parameter is set to Inherit: Same as product output. Therefore, you can see the product output data type calculated by the internal rule on the output signal in the model. The setting of the Accumulator parameter does not matter because this example uses real values.
For the preceding model, the Device type parameter in the Hardware Implementation pane of the Configuration Parameters dialog box is set to ASIC/FPGA. Therefore, the product data type used by the internal rule is the ideal, full-precision result.
Calculate the full-precision word length for each of the Array-Vector Multiply blocks in the model.
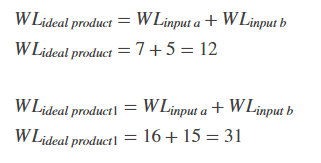
Calculate the full-precision fraction length, which is the same for each Array-Vector Multiply block in this example.
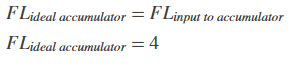
Now change the Device type parameter in the Hardware Implementation pane of the Configuration Parameters dialog box to 32-bit Embedded Processor, as shown in the following figure.
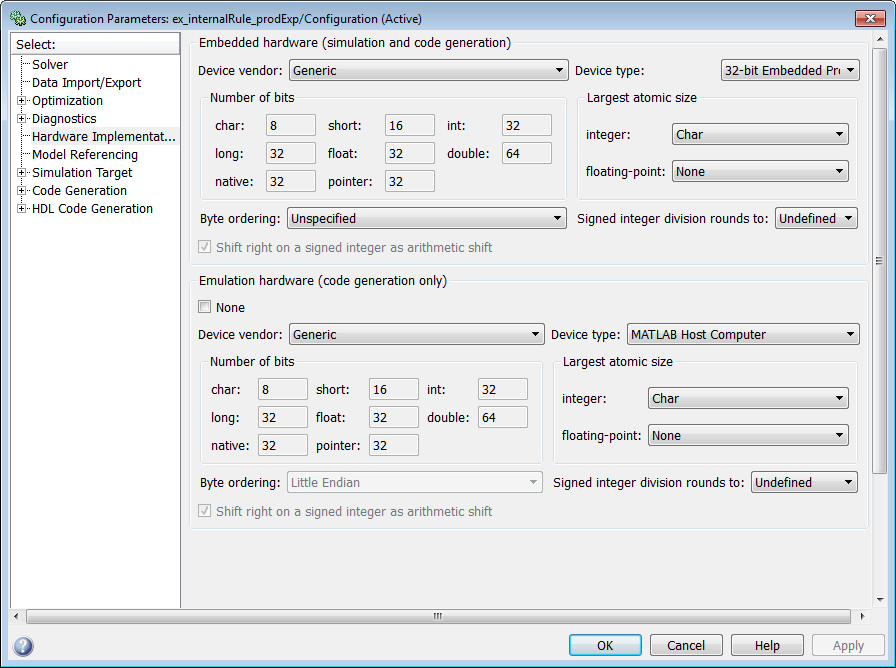
As you can see in the dialog box, this device has 8-, 16-, and 32-bit word lengths available. Therefore, the ideal word lengths of 12 and 31 bits calculated by the internal rule cannot be used. Instead, the internal rule uses the next largest available word length in each case. You can see this if you rerun the model, as shown in the following figure.
Specify Data Types for Fixed-Point Blocks
The following sections show you how to use the Fixed-Point Tool to select appropriate
data types for fixed-point blocks in the ex_fixedpoint_tut
model:
Prepare the Model
Open the ex_fixedpoint_tut model.
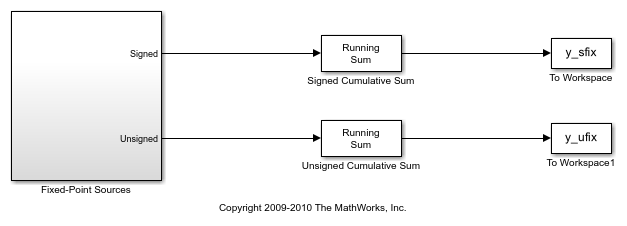
This model uses the Cumulative Sum block to sum the input coming from the Fixed-Point Sources subsystem. The Fixed-Point Sources subsystem outputs two signals with different data types:
The Signed source has a word length of 16 bits and a fraction length of 15 bits.
The Unsigned source has a word length of 16 bits and a fraction length of 16 bits.
Run the model to check for overflow. MATLAB displays the following warnings at the command line:
Warning: Overflow occurred. This originated from 'ex_fixedpoint_tut/Signed Cumulative Sum'. Warning: Overflow occurred. This originated from 'ex_fixedpoint_tut/Unsigned Cumulative Sum'.
According to these warnings, overflow occurs in both Cumulative Sum blocks.
To investigate the overflows in this model, use the Fixed-Point Tool. You can open the Fixed-Point Tool by selecting Tools > Fixed-Point > Fixed-Point Tool from the model menu. Turn on logging for all blocks in your model by setting the Fixed-point instrumentation mode parameter to Minimums, maximums and overflows.
Now that you have turned on logging, rerun the model by clicking the Simulation button.
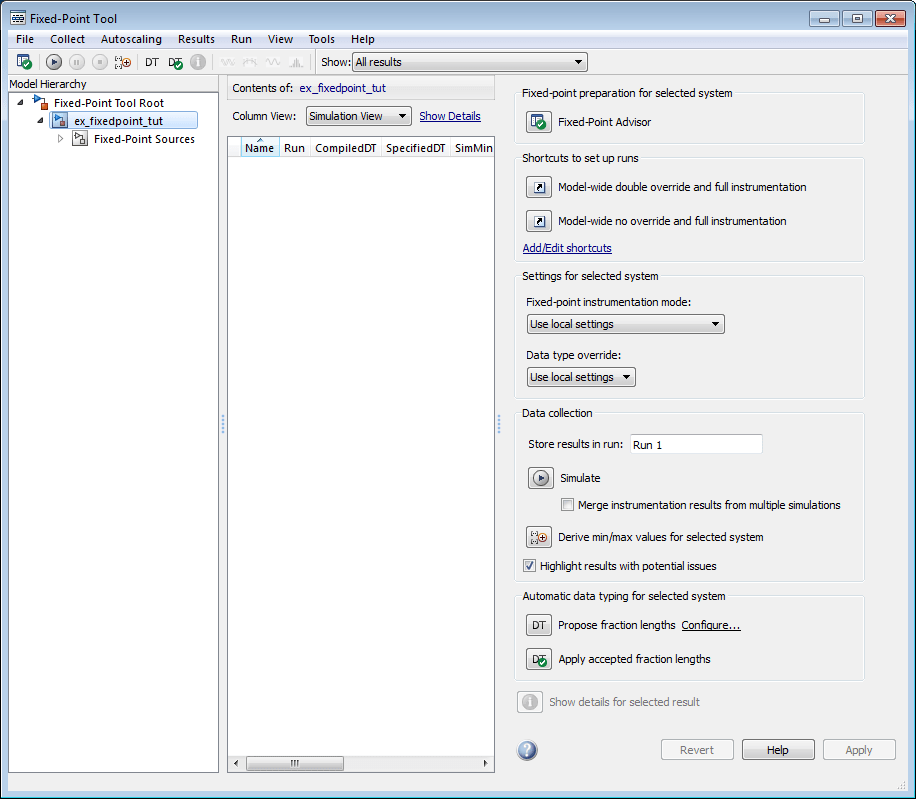
The results of the simulation appear in a table in the central Contents pane of the Fixed-Point Tool. Review the following columns:
Name: Provides the name of each signal in the following format:
Subsystem Name/Block Name: Signal Name.SimDT: The simulation data type of each logged signal.
SpecifiedDT: The data type specified on the block dialog for each signal.
SimMin: The smallest representable value achieved during simulation for each logged signal.
SimMax: The largest representable value achieved during simulation for each logged signal.
OverflowWraps: The number of overflows that wrap during simulation.
You can also see that the SimMin and SimMax values for the Accumulator data types range from 0 to .9997. The logged results indicate that 8,192 overflows wrapped during simulation in the Accumulator data type of the Signed Cumulative Sum block. Similarly, the Accumulator data type of the Unsigned Cumulative Sum block had 16,383 overflows wrap during simulation.
To get more information about each of these data types, highlight them in the Contents pane, and click the Show details for selected result button.

Assume a target hardware that supports 32-bit integers, and set the Accumulator word length in both Cumulative Sum blocks to 32. To do so, perform the following steps:
Right-click the
Signed Cumulative Sum: Accumulatorrow in the Fixed-Point Tool pane, and select Highlight Block In Model.Double-click the block in the model, and select the Data Types pane of the dialog box. Open the Data Type Assistant for Accumulator by clicking the Assistant button in the Accumulator data type row. Set the Mode to
Fixed Point. To see the representable range of the current specified data type, click the Fixed-point details link. The tool displays the representable maximum and representable minimum values for the current data type.
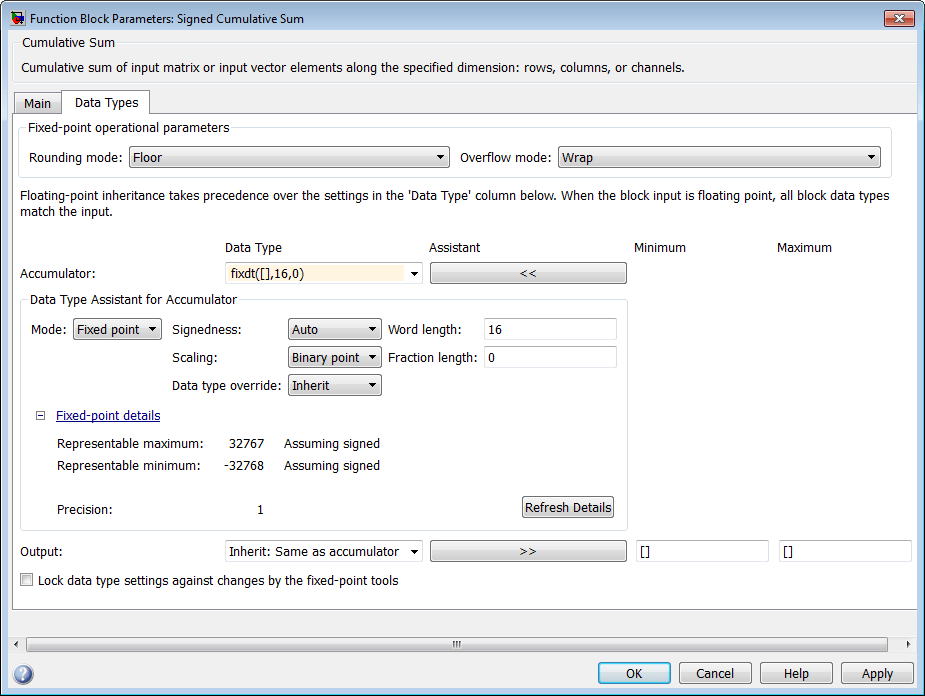
Change the Word length to 32, and click the Refresh details button in the Fixed-point details section to see the updated representable range. When you change the value of the Word length parameter, the Data Type edit box automatically updates.
Click OK on the block dialog box to save your changes and close the window.
Set the word length of the Accumulator data type of the Unsigned Cumulative Sum block to 32 bits. You can do so in one of two ways:
Type the data type
fixdt([],32,0)directly into Data Type edit box for the Accumulator data type parameter.Perform the same steps you used to set the word length of the Accumulator data type of the Signed Cumulative Sum block to 32 bits.
To verify your changes in word length and check for overflow, rerun your model. To do so, click the Simulate button in the Fixed-Point Tool.
The Contents pane of the Fixed-Point Tool updates, and you can see that no overflows occurred in the most recent simulation. However, you can also see that the SimMin and SimMax values range from 0 to 0. This underflow happens because the fraction length of the Accumulator data type is too small. The SpecifiedDT cannot represent the precision of the data values. The following sections discuss how to find a floating-point benchmark and use the Fixed-Point Tool to propose fraction lengths.
Use Data Type Override to Find a Floating-Point Benchmark
The Data type override feature of the Fixed-Point tool allows
you to override the data types specified in your model with floating-point types.
Running your model in Double override mode gives you a
reference range to help you select appropriate fraction lengths for your fixed-point
data types. To do so, perform the following steps:
Open the Fixed-Point Tool and set Data type override to
Double.Run your model by clicking the Run simulation and store active results button.
Examine the results in the Contents pane of the Fixed-Point Tool. Because you ran the model in
Doubleoverride mode, you get an accurate, idealized representation of the simulation minimums and maximums. These values appear in the SimMin and SimMax parameters.Now that you have an accurate reference representation of the simulation minimum and maximum values, you can more easily choose appropriate fraction lengths. Before making these choices, save your active results to reference so you can use them as your floating-point benchmark. To do so, select Results > Move Active Results To Reference from the Fixed-Point Tool menu. The status displayed in the Run column changes from
ActivetoReferencefor all signals in your model.
Use the Fixed-Point Tool to Propose Fraction Lengths
Now that you have your Double override results saved as
a floating-point reference, you are ready to propose fraction lengths.
To propose fraction lengths for your data types, you must have a set of
Activeresults available in the Fixed-Point Tool. To produce an active set of results, simply rerun your model. The tool now displays both theActiveresults and theReferenceresults for each signal.Select the Use simulation min/max if design min/max is not available check box. You did not specify any design minimums or maximums for the data types in this model. Thus, the tool uses the logged information to compute and propose fraction lengths. For information on specifying design minimums and maximums, see Specify Signal Ranges (Simulink).
Click the Propose fraction lengths button (
 ). The tool populates the proposed data
types in the ProposedDT column of the
Contents pane. The corresponding proposed minimums
and maximums are displayed in the ProposedMin and
ProposedMax columns.
). The tool populates the proposed data
types in the ProposedDT column of the
Contents pane. The corresponding proposed minimums
and maximums are displayed in the ProposedMin and
ProposedMax columns.
Examine the Results and Accept the Proposed Scaling
Before accepting the fraction lengths proposed by the Fixed-Point Tool, it is important to look at the details of that data type. Doing so allows you to see how much of your data the suggested data type can represent. To examine the suggested data types and accept the proposed scaling, perform the following steps:
In the Contents pane of the Fixed-Point Tool, you can see the proposed fraction lengths for the data types in your model.
The proposed fraction length for the Accumulator data type of both the Signed and Unsigned Cumulative Sum blocks is 17 bits.
To get more details about the proposed scaling for a particular data type, highlight the data type in the Contents pane of the Fixed-Point Tool.
Open the Autoscale Information window for the highlighted data type by clicking the Show autoscale information for the selected result button (
 ).
).
When the Autoscale Information window opens, check the Value and Percent Proposed Representable columns for the Simulation Minimum and Simulation Maximum parameters. You can see that the proposed data type can represent 100% of the range of simulation data.
To accept the proposed data types, select the check box in the Accept column for each data type whose proposed scaling you want to keep. Then, click the Apply accepted fraction lengths button (
 ). The tool updates the specified data
types on the block dialog boxes and the SpecifiedDT
column in the Contents pane.
). The tool updates the specified data
types on the block dialog boxes and the SpecifiedDT
column in the Contents pane.To verify the newly accepted scaling, set the Data type override parameter back to Use local settings, and run the model. Looking at Contents pane of the Fixed-Point Tool, you can see the following details:
The SimMin and SimMax values of the
Activerun match the SimMin and SimMax values from the floating-pointReferencerun.There are no longer any overflows.
The SimDT does not match the SpecifiedDT for the Accumulator data type of either Cumulative Sum block. This difference occurs because the Cumulative Sum block always inherits its Signedness from the input signal and only allows you to specify a Signedness of
Auto. Therefore, the SpecifiedDT for both Accumulator data types isfixdt([],32,17). However, because the Signed Cumulative Sum block has a signed input signal, the SimDT for the Accumulator parameter of that block is also signed (fixdt(1,32,17)). Similarly, the SimDT for the Accumulator parameter of the Unsigned Cumulative Sum block inherits its Signedness from its input signal and thus is unsigned (fixdt(0,32,17)).
