Tunable Lowpass Filtering of Noisy Input in Simulink
This example shows how to filter a noisy chirp signal with a lowpass filter that has a tunable passband frequency. The filter in this example is designed using a Variable Bandwidth IIR Filter block with Filter type set to Lowpass. This type of filter enables you to change the passband frequency during simulation without having to redesign the whole filter. The filter algorithm recomputes the filter coefficients whenever the passband frequency changes.
Open Lowpass Filter Model
Open the ex_tunable_chirp_lowpass model.
The input signal is a noisy chirp sampled at 44.1 kHz. The chirp has an initial frequency of 5000 Hz and a target frequency of 8000 Hz.
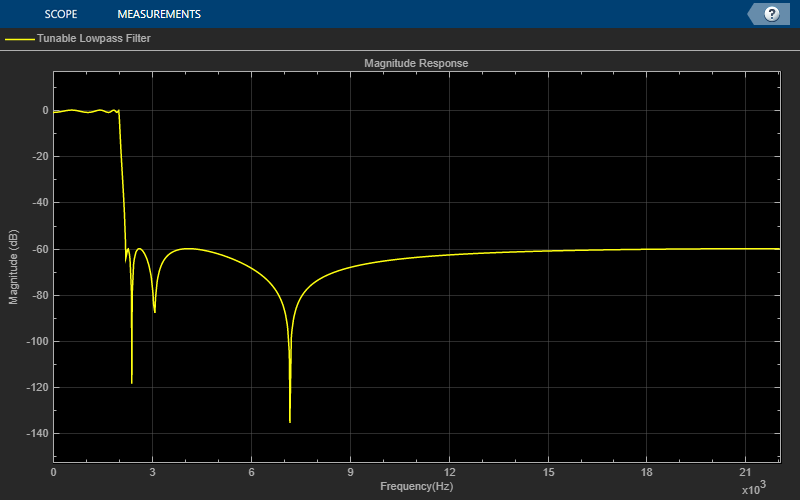
The Variable Bandwidth IIR Filter block has a lowpass frequency response, with the passband frequency set to 2000 Hz.
Simulate the Model
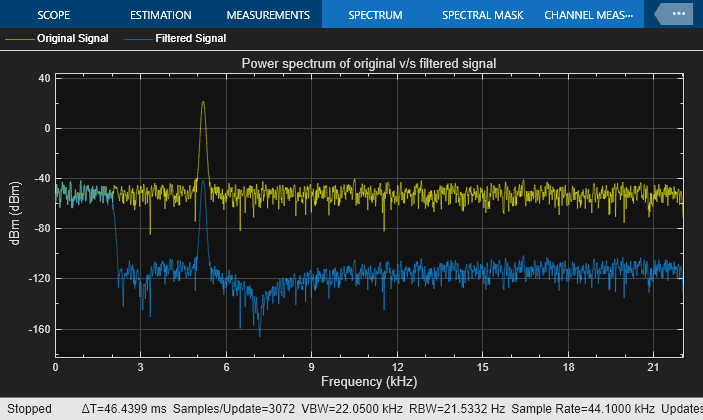
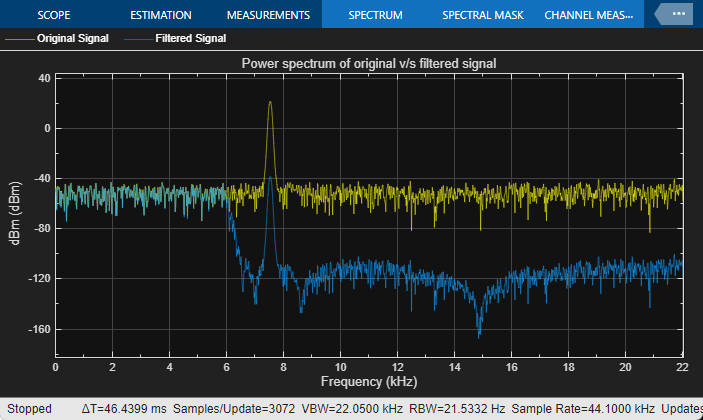
After you configure the block parameters, simulate the model. In the initial configuration, the chirp sweeps from 5000 Hz to 8000 Hz, which falls in the stopband of the filter. When the chirp input passes through this filter, the filter attenuates the chirp.
To tune the passband frequency of the filter, in the Variable Bandwidth IIR Filter block dialog box, change Filter passband frequency (Hz) to 6000 Hz while the simulation is running. Click Apply and the output of the Spectrum Analyzer changes immediately.
The chirp sweep frequency ranges from 5000 to 8000 Hz. Part of this frequency range is in the passband and the remaining part is in the stopband. While in the filter's passband frequency, the chirp is unaffected.
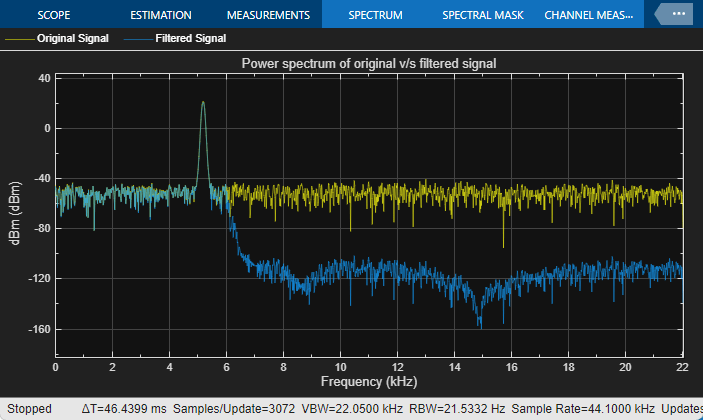
While in the filter's stopband frequency, the chirp is attenuated.
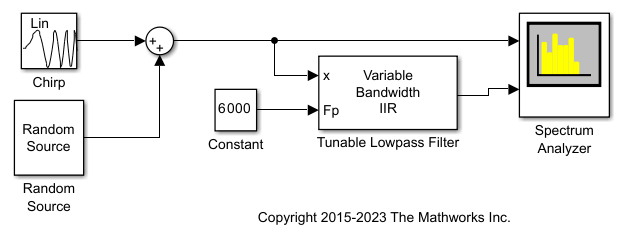
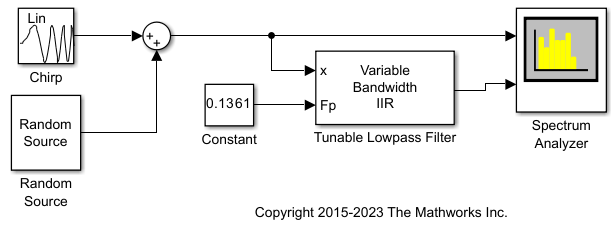
Tuning Frequency Specifications through Input Port
During simulation, you can tune the filter specifications such as the passband frequency, center frequency, and filter bandwidth through the input port, and see the impact on the filtered output in real time.
Using Normalized Frequency Units
You can provide the frequency specifications in normalized frequency units (ranging from 0 to 1) by setting the Sample rate mode parameter to Use normalized frequency (0 to 1).
See Also
Chirp | Random Source | Variable Bandwidth IIR Filter | Spectrum Analyzer
