collintest
Belsley collinearity diagnostics
Syntax
Description
[ displays, at the command window, Belsley collinearity diagnostics
for assessing the strength and sources of collinearity among variables in the input matrix
of time series data. The function also returns the singular
values in decreasing order, condition indices, and variance decomposition
proportions.sValue,condIdx,VarDecomp]
= collintest(X)
VarDecompTbl = collintest(Tbl)
To select a subset of variables, for which to compute collinearity diagnostics, use
the DataVariables name-value argument.
[___] = collintest(___,
specifies options using one or more name-value arguments in
addition to any of the input argument combinations in previous syntaxes.
Name=Value)collintest returns the output argument combination for the
corresponding input arguments. For example,
collintest(Tbl,Plot="on",Display="off",DataVariables=1:5) plots the
Belslely collinearity diagnostics for the first 5 variables of the table
Tbl to a figure instead of the command window.
collintest(
plots on the axes specified by ax,Plot="on",___)ax instead of
the current axes (gca). ax can precede any of the input
argument combinations in the previous syntaxes.
[___,
plots the diagnostics of the input series and additionally returns handles to plotted
graphics objects h]
= collintest(___,Plot="on")h. Use elements of h to modify
properties of the plot after you create it.
Examples
Compute Belsley Collinearity Diagnostics on Matrix of Data
Display collinearity diagnostics for multiple time series using the default options of collintest. Input the time series data as a numeric matrix.
Load data of Canadian inflation and interest rates Data_Canada.mat, which contains the series in the matrix Data.
load Data_CanadaDisplay the Belsley collinearity diagnostics at the command window. Return the singular values, condition indices, and variance decomposition proportions.
series'
ans = 5x1 cell
{'(INF_C) Inflation rate (CPI-based)' }
{'(INF_G) Inflation rate (GDP deflator-based)'}
{'(INT_S) Interest rate (short-term)' }
{'(INT_M) Interest rate (medium-term)' }
{'(INT_L) Interest rate (long-term)' }
[sValue,condIdx,VarDecomp] = collintest(Data);
Variance Decomposition sValue condIdx Var1 Var2 Var3 Var4 Var5 --------------------------------------------------------- 2.1748 1 0.0012 0.0018 0.0003 0.0000 0.0001 0.4789 4.5413 0.0261 0.0806 0.0035 0.0006 0.0012 0.1602 13.5795 0.3386 0.3802 0.0811 0.0011 0.0137 0.1211 17.9617 0.6138 0.5276 0.1918 0.0004 0.0193 0.0248 87.8245 0.0202 0.0099 0.7233 0.9979 0.9658
Only the last row in the display has a condition index larger than the default tolerance, 30. In this row, the last three variables (in the last three columns) have variance-decomposition proportions exceeding the default tolerance, 0.5. These results suggest that the short-, medium-, and long-term interest rates exhibit multicollinearity.
collintest organizes the outputs in the display table.
sValue
sValue = 5×1
2.1748
0.4789
0.1602
0.1211
0.0248
condIdx
condIdx = 5×1
1.0000
4.5413
13.5795
17.9617
87.8245
VarDecomp
VarDecomp = 5×5
0.0012 0.0018 0.0003 0.0000 0.0001
0.0261 0.0806 0.0035 0.0006 0.0012
0.3386 0.3802 0.0811 0.0011 0.0137
0.6138 0.5276 0.1918 0.0004 0.0193
0.0202 0.0099 0.7233 0.9979 0.9658
Compute Belsley Collinearity Diagnostics on Table Variables
Display and return collinearity diagnostics for multiple time series, which are variables in a table, using default options.
Load data of Canadian inflation and interest rates Data_Canada.mat. Convert the table DataTable to a timetable.
load Data_Canada dates = datetime(dates,ConvertFrom="datenum"); TT = table2timetable(DataTable,RowTimes=dates); TT.Observations = [];
Display the Belsley collinearity diagnostics, using all default options.
VarDecompTbl = collintest(TT)
Variance Decomposition sValue condIdx INF_C INF_G INT_S INT_M INT_L --------------------------------------------------------- 2.1748 1 0.0012 0.0018 0.0003 0.0000 0.0001 0.4789 4.5413 0.0261 0.0806 0.0035 0.0006 0.0012 0.1602 13.5795 0.3386 0.3802 0.0811 0.0011 0.0137 0.1211 17.9617 0.6138 0.5276 0.1918 0.0004 0.0193 0.0248 87.8245 0.0202 0.0099 0.7233 0.9979 0.9658
VarDecompTbl=5×7 table
sValue condIdx INF_C INF_G INT_S INT_M INT_L
________ _______ _________ _________ __________ __________ __________
2.1748 1 0.0012446 0.0017784 0.00033202 4.2326e-05 8.0328e-05
0.47889 4.5413 0.0261 0.080594 0.0034869 0.00057749 0.001159
0.16015 13.579 0.33864 0.38021 0.081126 0.0011166 0.013662
0.12108 17.962 0.61384 0.52756 0.19176 0.00035545 0.019308
0.024763 87.825 0.020173 0.0098575 0.72329 0.99791 0.96579
collintest returns collinearity diagnostics in the table VarDecompTbl, where variables correspond to the singular values, condition indices, and variance-decomposition proportions of each variable in the data (sValue, condIdx, and VarDecomp). The command window display and output table have a similar form.
By default, collintest computes collinearity diagnostics for all variables in the input table. To select a subset of variables from an input table, set the DataVariables option.
Extract the variance-decomposition proportions from the output table.
varnames = DataTable.Properties.VariableNames; VarDecomp = VarDecompTbl(:,varnames)
VarDecomp=5×5 table
INF_C INF_G INT_S INT_M INT_L
_________ _________ __________ __________ __________
0.0012446 0.0017784 0.00033202 4.2326e-05 8.0328e-05
0.0261 0.080594 0.0034869 0.00057749 0.001159
0.33864 0.38021 0.081126 0.0011166 0.013662
0.61384 0.52756 0.19176 0.00035545 0.019308
0.020173 0.0098575 0.72329 0.99791 0.96579
Plot Belsley Collinearity Diagnostics
Plot collinearity diagnostics for all time series in a table.
Load data of Canadian inflation and interest rates Data_Canada.mat.
load Data_CanadaPlot the Belsley collinearity diagnostics for all series.
collintest(DataTable,Plot="on");Variance Decomposition sValue condIdx INF_C INF_G INT_S INT_M INT_L --------------------------------------------------------- 2.1748 1 0.0012 0.0018 0.0003 0.0000 0.0001 0.4789 4.5413 0.0261 0.0806 0.0035 0.0006 0.0012 0.1602 13.5795 0.3386 0.3802 0.0811 0.0011 0.0137 0.1211 17.9617 0.6138 0.5276 0.1918 0.0004 0.0193 0.0248 87.8245 0.0202 0.0099 0.7233 0.9979 0.9658

The plot corresponds to the values in the last row of the variance-decomposition proportions, which are the only proportions with a condition index larger than the default tolerance of 30. The interest rate series have variance-decomposition proportions exceeding the default tolerance of 0.5 (red markers in the plot).
Plot Belsley Collinearity Diagnostics for Selected Variables and Intercept
Compute collinearity diagnostics for selected time series and an intercept.
Load the credit default data set Data_CreditDefaults.mat. The table DataTable contains the default rate of investment-grade corporate bonds series (IGD, the response variable) and several predictor variables.
load Data_CreditDefaultsConsider a multiple regression model for the default rate that includes an intercept term.
Include a variable in the table of data that represents the intercept in the design matrix (that is, a column of ones). Place the intercept variable at the beginning of the table.
Const = ones(height(DataTable),1); DataTable = addvars(DataTable,Const,Before=1);
Create a variable that contains all predictor variable names.
varnames = DataTable.Properties.VariableNames;
prednames = varnames(varnames ~= "IGD");Graph a correlation plot of all predictor variables except for the intercept dummy variable.
figure corrplot(DataTable,DataVariables=prednames(2:end), ... TestR="on");
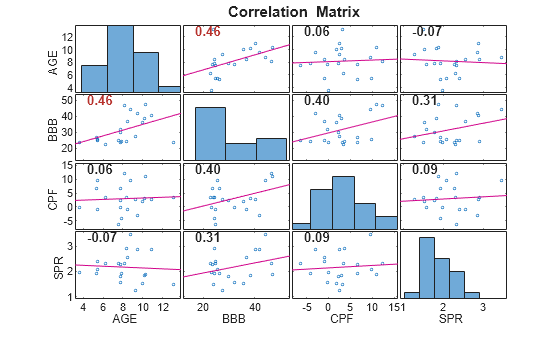
The predictor BBB is moderately linearly associated with the other predictors, while all other predictors appear unassociated with each other.
Plot the Belsley collinearity diagnostics of the predictor variables. Adjust the following options for the collinearity diagnostics:
Set the condition index tolerance to 10.
Set the variance-decomposition proportion tolerance to 0.5.
figure collintest(DataTable,Plot="on",DataVariables=prednames, ... TolIdx=10,TolProp=0.5);
Variance Decomposition sValue condIdx Const AGE BBB CPF SPR --------------------------------------------------------- 2.0605 1 0.0015 0.0024 0.0020 0.0140 0.0025 0.8008 2.5730 0.0016 0.0025 0.0004 0.8220 0.0023 0.2563 8.0400 0.0037 0.3208 0.0105 0.0004 0.3781 0.1710 12.0464 0.2596 0.0950 0.8287 0.1463 0.0001 0.1343 15.3405 0.7335 0.5793 0.1585 0.0173 0.6170
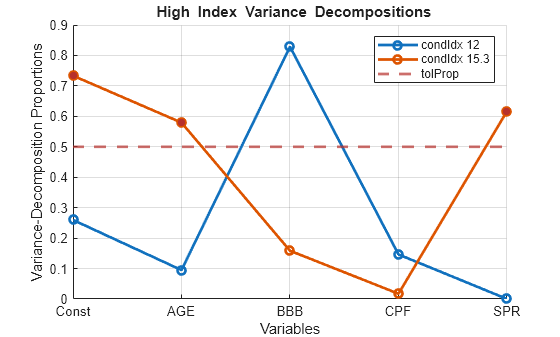
The row associated with condition index 12 (row 4) has one predictor (BBB) with a proportion above the tolerance 0.5, but collinearity requires two or more predictors for a dependency.
The row associated with condition index 15.3 (row 5) shows a weak dependence involving AGE, SPR, and the intercept, which the correlation plot does not expose.
Input Arguments
X — Time series data
numeric matrix
Time series data, specified as a numObs-by-numVars numeric matrix. Each column of X corresponds to a variable, and each row corresponds to an observation.
Data Types: double
Tbl — Time series data
table | timetable
Time series data, specified as a table or timetable with numObs rows. Each row of Tbl is an observation.
Specify numVars variables to include in the diagnostics computations by using the DataVariables argument. The selected variables must be numeric.
ax — Axes on which to plot
Axes object
Axes on which to plot, specified as an Axes object.
By default, collintest plots to the current axes (gca).
Note
To specify a model containing an intercept, include a variable (column) of ones in the time series data.
collintestscales all variables to unit length before computing diagnostics; do not center the variables in the data.Impute or remove all missing observations (indicated by
NaNentries) in the input data before passing the set tocollintest.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: collintest(Tbl,Plot="on",Display="off",DataVariables=1:5)
plots the Belslely collinearity diagnostics for the first 5 variables of the table
Tbl to a figure instead of the command window.
VarNames — Unique variable names used in displays and plots of results
string vector | character vector | cell vector of strings | cell vector of character vectors
Unique variable names used in displays and plots of the results, specified as a
string vector or cell vector of strings of a length numVars.
VarNames( specifies the name to
use for variable j)X(:, or
j)DataVariables(.j)
If an intercept term is present, VarNames must include the
intercept term (e.g., include the name "Const").
The software truncates all variable names to the first five characters.
If the input time series data is a matrix
X, the default is{'var1','var2',...}.If the input time series data is a table or timetable
Tbl, the default isTbl.Properties.VariableNames.
Example: VarNames=["Const" "AGE" "BBD"]
Data Types: char | cell | string
Display — Flag for command window display of results
"on" (default) | "off" | character vector
Flag for a command window display of results, specified as a value in this table.
| Value | Description |
|---|---|
"on" | collintest displays all outputs in tabular form
to the command window. |
"off" | collintest does not display the results to the
command window. |
Example: Display="off"
Data Types: char | string
Plot — Flag for plotting results
"off" (default) | "on" | character vector
Flag for plotting results to a figure, specified as a value in this table.
| Value | Description |
|---|---|
"on" |
If a
group of at least two variables in a critical row have variance-decomposition
proportions above the input tolerance |
"off" | collintest does not plot results to a figure.
|
Example: Plot="on"
Data Types: char | string
TolIdx — Condition index tolerance
30 (default) | numeric scalar of at least 1
Condition index tolerance, specified as a scalar value of at least 1.
collintest uses TolIdx to decide which
indices are large enough to infer a near dependency in the data.
TolIdx is used only when the Plot argument
is "on".
Example: TolIdx=25
Data Types: double
TolProp — Variance-decomposition proportion tolerance
0.5 (default) | numeric scalar in [0,1]
Variance-decomposition proportion tolerance, specified as a numeric scalar in the interval [0,1].
collintest uses TolProp to decide which
variables are involved in any near dependency. TolProp is used only
when the Plot argument is "on".
Example: TolProp=0.4
Data Types: double
DataVariables — Variables in Tbl
all variables (default) | string vector | cell vector of character vectors | vector of integers | logical vector
Variables in Tbl for which collintest
computes Belsley collinearity diagnostics, specified as a string vector or cell vector
of character vectors containing variable names in
Tbl.Properties.VariableNames, or an integer or logical vector
representing the indices of names. The selected variables must be numeric.
Example: DataVariables=["GDP" "CPI"]
Example: DataVariables=[true true false false] or
DataVariables=[1 2] selects the first and second table
variables.
Data Types: double | logical | char | cell | string
Output Arguments
sValue — Singular values
numeric vector
Singular values of the scaled
design matrix composed of the specified time series variables, returned as a numeric
vector with elements in descending order. collintest returns
sValue when you supply the input X.
condIdx — Condition indices
numeric vector
Condition indices, returned as a numeric vector with elements in ascending order.
All condition indices have value between 1 and the condition
number of the scaled design matrix of the specified time series variables.
collintest returns condIdx when you supply
the input X.
Large indices identify near dependencies among the specified variables. The size of the indices is a measure of how near dependencies are to collinearity.
VarDecomp — Variance-decomposition proportions
numeric matrix
Variance-decomposition
proportions, returned as a
numVars-by-numVars numeric matrix.
Large proportions, combined with a large condition index, identify groups of
variables involved in near dependencies. collintest returns
VarDecomp when you supply the input
X.
The size of the proportions is a measure of how badly the regression is degraded by the dependency.
VarDecompTbl — Collinearity diagnostics summary
table
h — Handles to plotted graphics objects
graphics array
Handles to plotted graphics objects, returned as a graphics array.
h contains unique plot identifiers, which you can use to query or
modify properties of the plot.
collintest plots only when you set
Plot="on".
More About
Belsley Collinearity Diagnostics
Belsley collinearity diagnostics assess the strength and sources of collinearity among variables in a multiple linear regression model.
To assess collinearity, the software computes singular values of the scaled variable matrix, X, and then converts them to condition indices. The conditional indices identify the number and strength of any near dependencies between variables in the variable matrix. The software decomposes the variance of the ordinary least squares (OLS) estimates of the regression coefficients in terms of the singular values to identify variables involved in each near dependency, and the extent to which the dependencies degrade the regression.
Condition Indices
The condition indices
(condIdx) for a scaled matrix X identify the
number and strength of any near dependencies in X.
For scaled matrix X with p columns and singular
values (sValue) , the condition indices of the columns of X are (sValue(1)/sValue(), where
j = 1,...,p.j)
All condition indices are bounded between one and the condition number.
Condition Number
The condition number of a scaled matrix X is an overall diagnostic for detecting collinearity.
For scaled matrix X with p columns and singular
values (sValue) , the condition number is (sValue(1)/sValue(end)).
The condition number achieves its lower bound of one when the columns of scaled X are orthonormal. The condition number rises as variates exhibit greater dependency.
A limitation of the condition number as a diagnostic is that it fails to provide specifics on the strength and sources of any near dependencies.
Multiple Linear Regression Model
A multiple linear regression model is a model of the form X is a design matrix of regression variables, and β is a vector of regression coefficients.
Singular Values
The singular values
(sValue) of a scaled matrix X are the diagonal
elements of the matrix S in the singular value decomposition
In descending order, the singular values of the scaled matrix X with p columns are .
Variance-Decomposition Proportions
Variance-decomposition proportions identify groups of variates involved in near dependencies, and the extent to which the dependencies degrade the regression.
From the singular value decomposition of scaled design matrix X (with p columns), define the following quantities:
V is the matrix of orthonormal eigenvectors of .
The singular values (
sValue) are the ordered diagonal elements of the matrix S.
The variance of the OLS estimate of multiple linear regression coefficient i, βi, is proportional to the sum
where denotes element (i,j) of V.
Variance-decomposition proportion (i,j)
(VarDecomp) is the proportion of term j in the sum
relative to the entire sum, j = 1,...,p.
The terms are the eigenvalues of scaled . Thus, large variance-decomposition proportions correspond to small eigenvalues of , a common diagnostic for collinearity. The singular value decomposition provides a more direct, numerically stable view of the eigensystem of scaled .
Tips
For purposes of collinearity diagnostics, Belsley [1] shows that column scaling of the design matrix composed of the input time series data is always desirable. However, he also shows that centering the data in
Xis undesirable. For models with an intercept, if you center the data inX, the role of the constant term in any near dependency is hidden, and yields misleading diagnostics.Tolerances for identifying large condition indices and variance-decomposition proportions are comparable to critical values in standard hypothesis tests. Experience determines the most useful tolerance, but experiments suggest the
collintestdefaults are good starting points [1].
References
[1] Belsley, D. A., E. Kuh, and R. E. Welsh. Regression Diagnostics. New York, NY: John Wiley & Sons, Inc., 1980.
[2] Judge, G. G., W. E. Griffiths, R. C. Hill, H. Lϋtkepohl, and T. C. Lee. The Theory and Practice of Econometrics. New York, NY: John Wiley & Sons, Inc., 1985.
Version History
Introduced in R2012aR2022a: collintest returns a results table when you supply a table of data
If you supply a table of time series data Tbl,
collintest returns a table containing variables for the singular
values sValue and condition indices condIdx, and
variables for the variance-decomposition proportions VarDecomp
associated with each time series, from which collinearity is diagnosed.
Before R2022a, collintest returned sValue,
condIdx, and VarDecomp in separate positions of
the output when you supplied a table of input data.
Starting in R2022a, if you supply a table of input data, update your code to return all
collinearity diagnostic outputs in the first output position. The second optional output is
the graphics object h.
[VarDecompTbl,h] = collintest(Tbl,Name=Value)
collintest issues an error if you request more outputs.
Also, access results by using table indexing. For more details, see Access Data in Tables.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)