lazy
Adjust Markov chain state inertia
Description
Examples
Create Lazy Markov Chain
Consider this three-state transition matrix.
Create the irreducible and periodic Markov chain that is characterized by the transition matrix P.
P = [0 1 0; 0 0 1; 1 0 0]; mc = dtmc(P);
At time t = 1,..., T, mc is forced to move to another state deterministically.
Determine the stationary distribution of the Markov chain and whether it is ergodic.
xFix = asymptotics(mc)
xFix = 1×3
0.3333 0.3333 0.3333
isergodic(mc)
ans = logical
0
mc is irreducible and not ergodic. As a result, mc has a stationary distribution, but it is not a limiting distribution for all initial distributions.
Show why xFix is not a limiting distribution for all initial distributions.
x0 = [1 0 0]; x1 = x0*P
x1 = 1×3
0 1 0
x2 = x1*P
x2 = 1×3
0 0 1
x3 = x2*P
x3 = 1×3
1 0 0
sum(x3 == x0) == mc.NumStates
ans = logical
1
The initial distribution is reached again after several steps, which implies that the subsequent state distributions cycle through the same sets of distributions indefinitely. Therefore, mc does not have a limiting distribution.
Create a lazy version of the Markov chain mc.
lc = lazy(mc)
lc =
dtmc with properties:
P: [3x3 double]
StateNames: ["1" "2" "3"]
NumStates: 3
lc.P
ans = 3×3
0.5000 0.5000 0
0 0.5000 0.5000
0.5000 0 0.5000
lc is a dtmc object. At time t = 1,..., T, lc "flips a fair coin". It remains in its current state if the "coin shows heads" and transitions to another state if the "coin shows tails".
Determine the stationary distribution of the lazy chain and whether it is ergodic.
lcxFix = asymptotics(lc)
lcxFix = 1×3
0.3333 0.3333 0.3333
isergodic(lc)
ans = logical
1
lc and mc have the same stationary distributions, but only lc is ergodic. Therefore, the limiting distribution of lc exists and is equal to its stationary distribution.
Supply Inertial Weights for Lazy Chain Transformation
Consider this theoretical, right-stochastic transition matrix of a stochastic process.
Create the Markov chain that is characterized by the transition matrix P.
P = [ 0 0 1/2 1/4 1/4 0 0 ;
0 0 1/3 0 2/3 0 0 ;
0 0 0 0 0 1/3 2/3;
0 0 0 0 0 1/2 1/2;
0 0 0 0 0 3/4 1/4;
1/2 1/2 0 0 0 0 0 ;
1/4 3/4 0 0 0 0 0 ];
mc = dtmc(P);Plot the eigenvalues of the transition matrix on the complex plane.
figure;
eigplot(mc);
title('Original Markov Chain')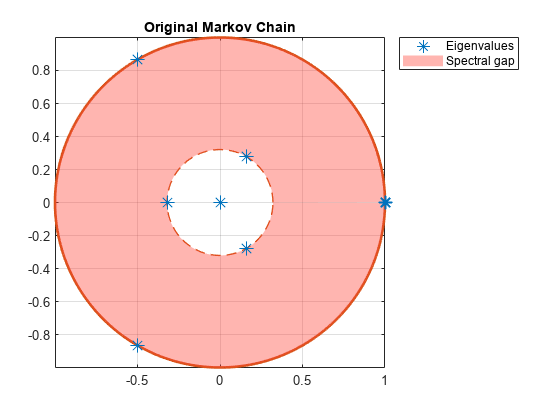
Three eigenvalues have modulus one, which indicates that the period of mc is three.
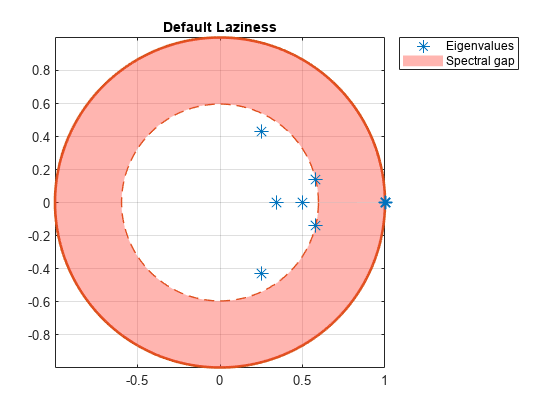
Create lazy versions of the Markov chain mc using various inertial weights. Plot the eigenvalues of the lazy chains on separate complex planes.
w2 = 0.1; % More active Markov chain w3 = 0.9; % Lazier Markov chain w4 = [0.9 0.1 0.25 0.5 0.25 0.001 0.999]; % Laziness differs between states lc1 = lazy(mc); lc2 = lazy(mc,w2); lc3 = lazy(mc,w3); lc4 = lazy(mc,w4); figure; eigplot(lc1); title('Default Laziness');
figure;
eigplot(lc2);
title('More Active Chain');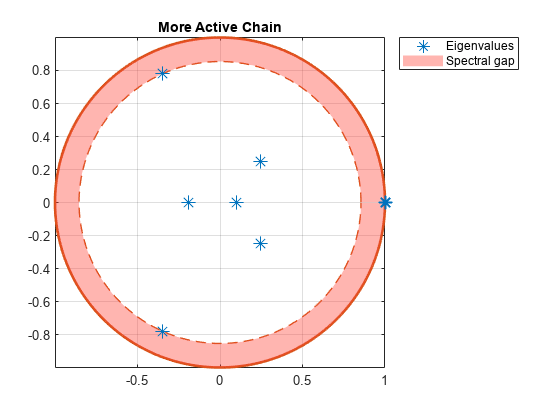
figure;
eigplot(lc3);
title('Lazier Chain');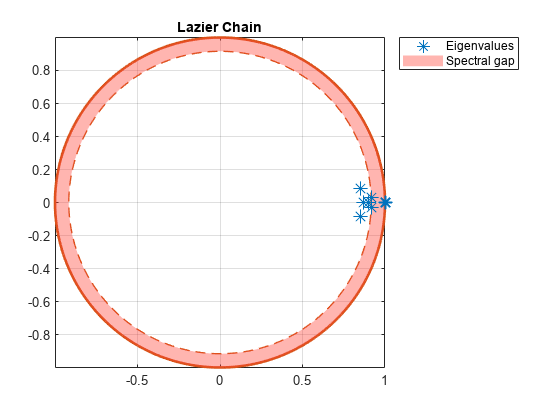
figure;
eigplot(lc4);
title('Differing Laziness Levels');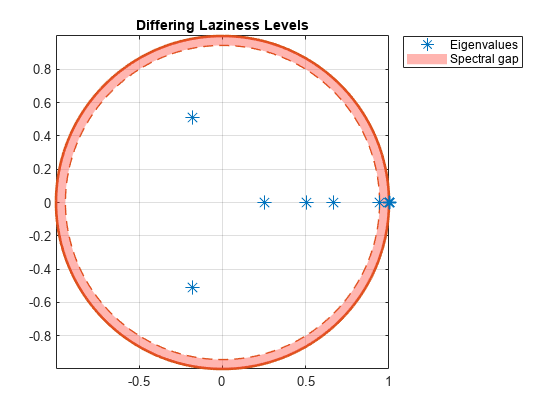
All lazy chains have only one eigenvalue with modulus one. Therefore, they are aperiodic. The spectral gap (distance between inner and outer circle) determines the mixing time. Observe that all lazy chains take longer to mix than the original Markov chain. Chains with different inertial weights than the default take longer to mix than the default lazy chain.
Input Arguments
mc — Discrete-time Markov chain
dtmc object
Discrete-time Markov chain with NumStates states and transition matrix P, specified as a dtmc object. P must be fully specified (no NaN entries).
w — Inertial weights
0.5 (default) | numeric scalar | numeric vector
Inertial weights, specified as a numeric scalar or vector of length NumStates. Values must be between 0 and 1.
If
wis a scalar,lazyapplies it to all states. That is, the transition matrix of the lazy chain (lc.P) is the result of the linear transformationP is
mc.Pand I is theNumStates-by-NumStatesidentity matrix.If
wis a vector,lazyapplies the weights state by state (row by row).
Data Types: double
Output Arguments
More About
Lazy Chain
A lazy version of a Markov chain has, for each state, a probability of staying in the same state equal to at least 0.5.
In a directed graph of a Markov chain, the default lazy transformation ensures self-loops on all states, eliminating periodicity. If the Markov chain is irreducible, then its lazy version is ergodic. See graphplot.
References
[1] Gallager, R.G. Stochastic Processes: Theory for Applications. Cambridge, UK: Cambridge University Press, 2013.
Version History
Introduced in R2017b
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)