Simulate Conditional Variance Model
This example shows how to simulate a conditional variance model using simulate.
Step 1. Load the data and specify the model.
Load the Deutschmark/British pound foreign exchange rate data included with the toolbox, and convert to returns. Specify and fit a GARCH(1,1) model.
load Data_MarkPound
r = price2ret(Data);
T = length(r);
Mdl = garch(1,1);
EstMdl = estimate(Mdl,r);
GARCH(1,1) Conditional Variance Model (Gaussian Distribution):
Value StandardError TStatistic PValue
__________ _____________ __________ __________
Constant 1.0538e-06 3.5052e-07 3.0062 0.0026452
GARCH{1} 0.80654 0.012913 62.462 0
ARCH{1} 0.15438 0.011577 13.335 1.4436e-40
v0 = infer(EstMdl,r);
Step 2. Simulate foreign exchange rate returns.
Use the fitted model to simulate 25 realizations of foreign exchange rate returns and conditional variances over a 1000-period forecast horizon. Use the observed returns and inferred conditional variances as presample innovations and variances, respectively.
rng default; % For reproducibility [V,Y] = simulate(EstMdl,1000,'NumPaths',25,... 'E0',r,'V0',v0); figure subplot(2,1,1) plot(v0) hold on plot(T+1:T+1000,V) xlim([0,T+1000]) title('Conditional Variances') hold off subplot(2,1,2) plot(r) hold on plot(T+1:T+1000,Y) xlim([0,T+1000]) title('Returns') hold off
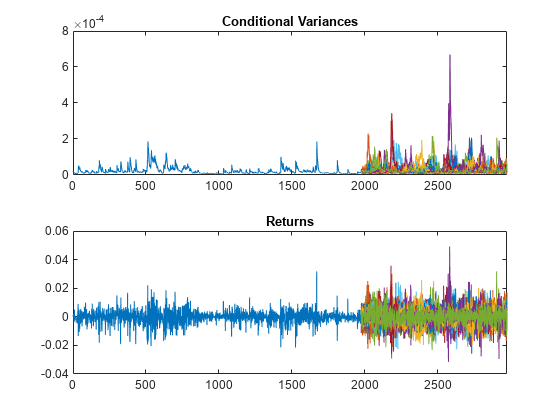
Step 3. Plot the returns distribution at a future time.
Use simulations to generate a forecast distribution of foreign exchange returns 500 days into the future. Generate 1000 sample paths to estimate the distribution.
rng default; % For reproducibility [V,Y] = simulate(EstMdl,500,'NumPaths',1000,... 'E0',r-EstMdl.Offset,'V0',v0); figure histogram(Y(500,:),10) title('Return Distribution in 500 Days')
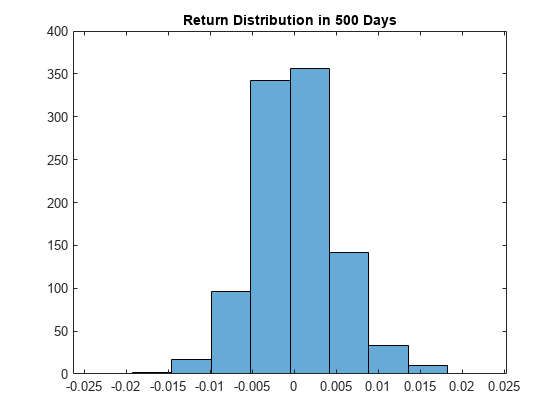
See Also
Objects
Functions
Related Examples
- Specify Conditional Variance Model for Exchange Rates
- Likelihood Ratio Test for Conditional Variance Models
- Forecast a Conditional Variance Model
