refine
Refine initial parameters to aid state-space model estimation
Description
refine( finds
a set of initial parameter values to use when fitting the state-space
model Mdl,Y,params0)Mdl to the response data Y,
using the crude set of initial parameter values params0.
The software uses several routines, and displays the resulting loglikelihood
and initial parameter values for each routine.
refine( displays
results of the routines with additional options specified by one or
more Mdl,Y,params0,Name,Value)Name,Value pair arguments. For example,
you can include a linear regression component composed of predictors
and an initial value for the coefficients.
Output = refine(___)Output) containing a vector
of refined, initial parameter values, the loglikelihood corresponding
the initial parameter values, and the method the software used to
obtain the values. You can use any of the input arguments in the previous
syntaxes.
Examples
Refine Parameters When Fitting Time-Invariant State-Space Model
Suppose that a latent process is a random walk. The state equation is
where is Gaussian with mean 0 and standard deviation 1.
Generate a random series of 100 observations from , assuming that the series starts at 1.5.
T = 100;
rng(1); % For reproducibility
u = randn(T,1);
x = cumsum([1.5;u]);
x = x(2:end);Suppose further that the latent process is subject to additive measurement error. The observation equation is
where is Gaussian with mean 0 and standard deviation 1.
Use the random latent state process (x) and the observation equation to generate observations.
y = x + randn(T,1);
Together, the latent process and observation equations compose a state-space model. Assume that the state is a stationary AR(1) process. Then the state-space model to estimate is
Specify the coefficient matrices. Use NaN values for unknown parameters.
A = NaN; B = NaN; C = 1; D = NaN;
Specify the state-space model using the coefficient matrices. Specify that the initial state distribution is stationary using the StateType name-value pair argument.
StateType = 0;
Mdl = ssm(A,B,C,D,'StateType',StateType);Mdl is an ssm model. The software sets values for the initial state mean and variance. Verify that the model is specified correctly using the display in the Command Window.
Pass the observations to estimate to estimate the parameters. For the params0 parameters that are unlikely to correspond to their true values. Also, specify lower bound constraints of 0 for the standard deviations.
params0 = [-1e7 1e-6 2000];
EstMdl = estimate(Mdl,y,params0,'lb',[-Inf,0,0]);Warning: Covariance matrix of estimators cannot be computed precisely due to inversion difficulty. Check parameter identifiability. Also try different starting values and other options to compute the covariance matrix.
Method: Maximum likelihood (fmincon)
Sample size: 100
Logarithmic likelihood: -2464.23
Akaike info criterion: 4934.46
Bayesian info criterion: 4942.27
| Coeff Std Err t Stat Prob
------------------------------------------------------------
c(1) | -9.99977e+06 9.99977e+05 -10.00000 0
c(2) | 1.23086e+05 1.91161e+13 0.00000 1.00000
c(3) | 2006.86501 3.11680e+11 0.00000 1.00000
|
| Final State Std Dev t Stat Prob
x(1) | -3.37649 1999.42392 -0.00169 0.99865
estimate failed to converge, and so the results are undesirable.
Refine params0 using refine.
Output = refine(Mdl,y,params0);
logL = cell2mat({Output.LogLikelihood})';
[~,maxLogLIndx] = max(logL)maxLogLIndx = 2
refinedParams0 = Output(maxLogLIndx).Parameters
refinedParams0 = 1×3
0.9705 -0.8934 0.9330
Description = Output(maxLogLIndx).Description
Description = 'Nelder-Mead simplex'
The algorithm that yields the highest loglikelihood value is Loose bound interior point, which is the third struct in the structure array Output.
Estimate Mdl using refinedParams0, which is the vector of refined initial parameter values.
EstMdl = estimate(Mdl,y,refinedParams0,'lb',[-Inf,0,0]);Method: Maximum likelihood (fmincon)
Sample size: 100
Logarithmic likelihood: -181.379
Akaike info criterion: 368.758
Bayesian info criterion: 376.574
| Coeff Std Err t Stat Prob
---------------------------------------------------
c(1) | 0.97050 0.02863 33.90368 0
c(2) | 0.89343 0.18521 4.82401 0.00000
c(3) | 0.93303 0.15176 6.14806 0
|
| Final State Std Dev t Stat Prob
x(1) | -3.93007 0.72066 -5.45343 0
estimate converged, making the parameter estimates much more desirable. The AR model coefficient is within two standard errors of 1, which suggests that the state processes is a random walk.
Refine Estimation of State-Space Model Containing Regression Component
Suppose that the relationship between the unemployment rate and the nominal gross national product (nGNP) is linear. Suppose further that the unemployment rate is an AR(1) series. Symbolically, and in state-space form, the model is

where:
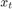 is the unemployment rate at time t.
is the unemployment rate at time t.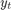 is the observed unemployment rate being deflated by the log of nGNP (
is the observed unemployment rate being deflated by the log of nGNP (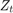 ).
).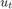 is the Gaussian series of state disturbances having mean 0 and unknown standard deviation
is the Gaussian series of state disturbances having mean 0 and unknown standard deviation  .
.
Load the Nelson-Plosser data set, which contains the unemployment rate and nGNP series data.
load Data_NelsonPlosser
Preprocess the data by taking the first difference of the unemployment rate and converting nGNP to a series of returns. Remove the observations corresponding to the sequence of NaN values at the beginning of the unemployment rate series.
isNaN = any(ismissing(DataTable),2); % Flag periods containing NaNs
gnpn = DataTable.GNPN(~isNaN);
y = DataTable.UR(~isNaN);
y = diff(y);
T = size(y,1);
Z = [ones(T,1) price2ret(gnpn)];
This example continues using the series without NaN values. However, using the Kalman filter framework, the software can accommodate series containing missing values.
Specify the coefficient matrices.
A = NaN; B = NaN; C = 1;
Specify the state-space model using ssm.
Mdl = ssm(A,B,C);
Find a good set of starting parameters to use for estimation.
params0 = [150 1000]; % Initial values chosen arbitrarily Beta0 = [1 -100]; Output = refine(Mdl,y,params0,'Predictors',Z,'Beta0',Beta0);
Output is a 1-by-5 structure array containing the recommended initial parameter values.
Choose the initial parameter values corresponding to the largest loglikelihood.
logL = cell2mat({Output.LogLikelihood})';
[~,maxLogLIndx] = max(logL)
refinedParams0 = Output(maxLogLIndx).Parameters
Description = Output(maxLogLIndx).Description
maxLogLIndx =
2
refinedParams0 =
0.0000 -1.3441 1.3477 -24.4336
Description =
'Nelder-Mead simplex'
Estimate Mdl using the refined initial parameter values refinedParams0.
EstMdl = estimate(Mdl,y,refinedParams0(1:(end - 2)),'Predictors',Z,... 'Beta0',refinedParams0((end - 1):end));
Method: Maximum likelihood (fminunc)
Sample size: 61
Logarithmic likelihood: -103.321
Akaike info criterion: 214.642
Bayesian info criterion: 223.085
| Coeff Std Err t Stat Prob
----------------------------------------------------------
c(1) | 0.20499 0.12217 1.67793 0.09336
c(2) | -1.31586 0.08283 -15.88649 0
y <- z(1) | 1.38082 0.23315 5.92241 0
y <- z(2) | -24.87986 1.76909 -14.06365 0
|
| Final State Std Dev t Stat Prob
x(1) | 1.19607 0 Inf 0
estimate returns reasonable parameter estimates and their corresponding standard errors.
Input Arguments
Mdl — Standard state-space model
ssm model object
Standard state-space model containing unknown parameters, specified
as an ssm model object returned by ssm.
For explicitly created state-space models, the software estimates all
NaNvalues in the coefficient matrices (Mdl.A,Mdl.B,Mdl.C, andMdl.D) and the initial state means and covariance matrix (Mdl.Mean0andMdl.Cov0). For details on explicit and implicit model creation, seessm.For implicitly created state-space models, you specify the model structure and the location of the unknown parameters using the parameter-to-matrix mapping function. Implicitly create a state-space model to estimate complex models, impose parameter constraints, and estimate initial states. The parameter-to-mapping function can also accommodate additional output arguments.
Note
Mdl does not store observed responses or
predictor data. Supply the data wherever necessary, using the appropriate
input and name-value pair arguments.
Y — Observed response data
numeric matrix | cell vector of numeric vectors
Observed response data to which Mdl is fit,
specified as a numeric matrix or a cell vector of numeric vectors.
If
Mdlis time invariant with respect to the observation equation, thenYis a T-by-n matrix. Each row of the matrix corresponds to a period and each column corresponds to a particular observation in the model. Therefore, T is the sample size and n is the number of observations per period. The last row ofYcontains the latest observations.If
Mdlis time varying with respect to the observation equation, thenYis a T-by-1 cell vector.Y{t}contains an nt-dimensional vector of observations for period t, where t = 1,...,T. The corresponding dimensions of the coefficient matrices inMdl.C{t}andMdl.D{t}must be consistent with the matrix inY{t}for all periods. The last cell ofYcontains the latest observations.
Suppose that you create Mdl implicitly by
specifying a parameter-to-matrix mapping function, and the function
has input arguments for the observed responses or predictors. Then,
the mapping function establishes a link to observed responses and
the predictor data in the MATLAB® workspace, which overrides the
value of Y.
NaN elements indicate missing observations.
For details on how the Kalman filter accommodates missing observations,
see Algorithms.
Data Types: double | cell
params0 — Initial values of unknown parameters
numeric vector
Initial values of unknown parameters for numeric maximum likelihood estimation, specified as a numeric vector.
The elements of params0 correspond to the
unknown parameters in the state-space model matrices A, B, C,
and D, and, optionally, the initial state mean Mean0 and
covariance matrix Cov0.
If you created
Mdlexplicitly (that is, by specifying the matrices without a parameter-to-matrix mapping function), then the software maps the elements ofparamstoNaNs in the state-space model matrices and initial state values. The software searches forNaNs column-wise, following the orderA,B,C,D,Mean0,Cov0.If you created
Mdlimplicitly (that is, by specifying the matrices with a parameter-to-matrix mapping function), then set initial parameter values for the state-space model matrices, initial state values, and state types within the parameter-to-matrix mapping function.
Data Types: double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: refine(Mdl,Y,params0,'Beta0',RC)
Beta0 — Initial values of regression coefficients
numeric matrix
Initial values of regression coefficients, specified as the
comma-separated pair consisting of 'Beta0' and
a d-by-n numeric matrix. d is
the number of predictor variables (see Predictors)
and n is the number of observed response series
(see Y).
By default, Beta0 is the ordinary least-squares
estimate of Y onto Predictors.
Data Types: double
Predictors — Predictor data
[] (default) | numeric matrix
Predictor data for the regression component in the observation
equation, specified as the comma-separated pair consisting of 'Predictors' and
a T-by-d numeric matrix. T is
the number of periods and d is the number of predictor
variables. Row t corresponds to the observed predictors
at period t (Zt)
in the expanded observation equation
In other words, the predictor series serve as observation deflators. β is a d-by-n time-invariant matrix of regression coefficients that the software estimates with all other parameters.
For n observations per period, the software regresses all predictor series onto each observation.
If you specify
Predictors, thenMdlmust be time invariant. Otherwise, the software returns an error.By default, the software excludes a regression component from the state-space model.
Data Types: double
Output Arguments
Output — Information about initial parameter values
structure array
Information about the initial parameter values, returned as
a 1-by-5 structure array. The software uses five algorithms to find
initial parameter values, and each element of Output corresponds
to an algorithm.
This table describes the fields of Output.
| Field | Description | |||||
|---|---|---|---|---|---|---|
Description | Refinement algorithm. Each element of
| |||||
Loglikelihood | Loglikelihood corresponding to the initial parameter values. | |||||
Parameters | Vector of refined initial parameter values. The order of the
parameters is the same as the order in params0.
If you pass these initial values to estimate, then
the estimation results can improve. |
Tips
Likelihood surfaces of state-space models can be complicated, for example, they might contain multiple local maxima. If
estimatefails to converge, or converges to an unsatisfactory solution, thenrefinemight find a better set of initial parameter values to pass toestimate.The refined initial parameter values returned by
refinemight appear similar to each other and toparams0. Choose a set yielding estimates that make economic sense and correspond to relatively large loglikelihood values.If a refinement attempt fails, then the software displays errors and sets the corresponding loglikelihood to
-Inf. It also sets its initial parameter values to[].
Algorithms
The Kalman filter accommodates missing data by not updating filtered state estimates corresponding to missing observations. In other words, suppose that your data has a missing observation at period t. Then, the state forecast for period t, based on the previous t – 1 observations, is equivalent to the filtered state for period t.
Version History
Introduced in R2014a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)