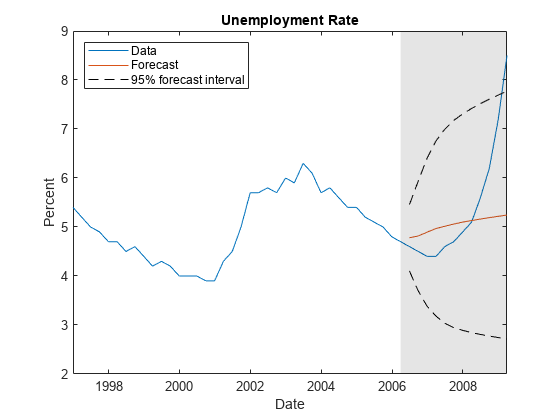
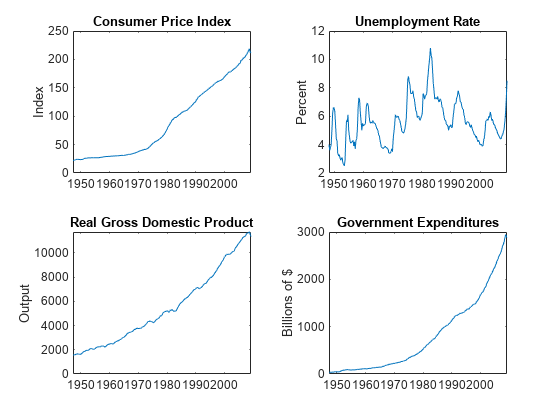
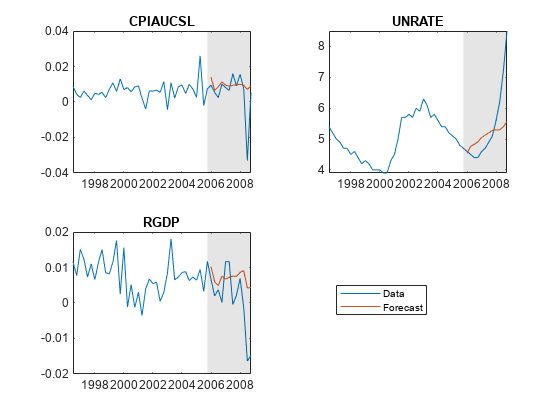
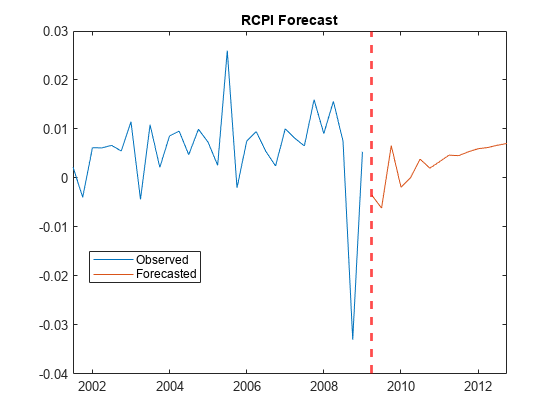
forecast
Forecast vector autoregression (VAR) model responses
Syntax
Description
Conditional and Unconditional Forecasts for Numeric Arrays
Y = forecast(Mdl,numperiods,Y0)Y over a length
numperiods forecast horizon, using the fully specified
VAR(p) model Mdl. The forecasted
responses represent the continuation of the presample data in the numeric array
Y0.
Y = forecast(Mdl,numperiods,Y0,Name=Value)forecast returns numeric arrays when all optional
input data are numeric arrays. For example,
forecast(Mdl,10,Y0,X=Exo) returns a numeric array
containing a 10-period forecasted response path from Mdl
and the numeric matrix of presample response data Y0, and
specifies the numeric matrix of future predictor data for the model regression
component in the forecast horizon Exo.
To produce a conditional forecast, specify future response data in a numeric
array by using the YF name-value argument.
Unconditional Forecasts for Tables and Timetables
Tbl2 = forecast(Mdl,numperiods,Tbl1)Tbl2 containing the length
numperiods paths of multivariate MMSE response variable
forecasts, which result from computing unconditional forecasts from the VAR
model Mdl. forecast uses the table
or timetable of presample data Tbl1 to initialize the
response series. (since R2022b)
forecast selects the variables in
Mdl.SeriesNames to forecast, or it selects all variables
in Tbl1. To select different response variables in
Tbl1 to forecast, use the
PresampleResponseVariables name-value argument.
Tbl2 = forecast(Mdl,numperiods,Tbl1,Name=Value)forecast(Mdl,10,Tbl1,PresampleResponseVariables=["GDP"
"CPI"]) returns a timetable of response variables containing their
unconditional forecasts from the VAR model Mdl, initialized
by the data in the GDP and CPI variables
of the timetable of presample data in Tbl1. (since R2022b)
Conditional Forecasts for Tables and Timetables
Tbl2 = forecast(Mdl,numperiods,Tbl1,InSample=InSample,ResponseVariables=ResponseVariables)Tbl2 containing the length
numperiods paths of multivariate MMSE response variable
forecasts and corresponding forecast MSEs, which result from computing
conditional forecasts from the VAR model Mdl.
forecast uses the table or timetable of presample
data Tbl1 to initialize the response series.
InSample is a table or timetable of future data in the
forecast horizon that forecast uses to compute
conditional forecasts and ResponseVariables specifies the
response variables in InSample. (since R2022b)
Tbl2 = forecast(Mdl,numperiods,Tbl1,InSample=InSample,ResponseVariables=ResponseVariables,Name=Value)
Examples
Input Arguments
Output Arguments
Algorithms
forecastestimates unconditional forecasts using the equationwhere t = 1,...,
numperiods.forecastfilters anumperiods-by-numseriesmatrix of zero-valued innovations throughMdl.forecastuses specified presample innovations (Y0orTbl1) wherever necessary.forecastestimates conditional forecasts using the Kalman filter.forecastrepresents the VAR modelMdlas a state-space model (ssmmodel object) without observation error.forecastfilters the forecast dataYFthrough the state-space model. At period t in the forecast horizon, any unknown response iswhere s < t, is the filtered estimate of y from period s in the forecast horizon.
forecastuses specified presample values inY0orTbl1for periods before the forecast horizon.
The way
forecastdeterminesnumpaths, the number of paths (pages) in the output argumentY, or the number of paths (columns) in the forecasted response variables in the output argumentTbl2, depends on the forecast type.If you estimate unconditional forecasts, which means you do not specify the
YFname-value argument, orInSampleandResponseVariablesname-value arguments,numpathsis the number of paths in theY0orTbl1input argument.If you estimate conditional forecasts and the presample data
Y0and future sample dataYF, or response variables inTbl1andInSamplehave more than one path,numpathsis the fewest number of paths between the presample and future sample response data. Consequently,forecastuses only the firstnumpathspaths of each response variable for each input.If you estimate conditional forecasts and either
Y0orYF, or response variables inTbl1orInSamplehave one path,numpathsis the number of pages in the array with the most pages.forecastuses the variables with one path to produce each output path.
forecastsets the time origin of models that include linear time trends t0 tonumpreobs–Mdl.P(after removing missing values), wherenumpreobsis the number of presample observations. Therefore, the times in the trend component are t = t0 + 1, t0 + 2,..., t0 +numpreobs. This convention is consistent with the default behavior of model estimation in whichestimateremoves the firstMdl.Presponses, reducing the effective sample size. Althoughforecastexplicitly uses the firstMdl.Ppresample responses inY0orTbl1to initialize the model, the total number of usable observations determines t0. An observation inY0is usable if it does not contain aNaN.
References
[1] Hamilton, James D. Time Series Analysis. Princeton, NJ: Princeton University Press, 1994.
[2] Johansen, S. Likelihood-Based Inference in Cointegrated Vector Autoregressive Models. Oxford: Oxford University Press, 1995.
[3] Juselius, K. The Cointegrated VAR Model. Oxford: Oxford University Press, 2006.
[4] Lütkepohl, H. New Introduction to Multiple Time Series Analysis. Berlin: Springer, 2005.