vecm
Create vector error-correction (VEC) model
Description
The vecm function returns a vecm object specifying the functional form and storing the parameter values of a (p – 1)-order, cointegrated, multivariate vector error-correction model (VEC((p – 1)) model.
The key components of a vecm object include the number of time series (response-variable dimensionality), the number of cointegrating relations among the response variables (cointegrating rank), and the degree of the multivariate autoregressive polynomial composed of first differences of the response series (short-run polynomial), which is p – 1. That is, p – 1 is the maximum lag with a nonzero coefficient matrix, and p is the order of the vector autoregression (VAR) model representation of the VEC model. Other model components include a regression component to associate the same exogenous predictor variables to each response series, and constant and time trend terms.
Another important component of a VEC model is its Johansen form because it dictates how MATLAB® includes deterministic terms in the model. This specification has implications on the estimation procedure and allowable equality constraints. For more details, see Johansen Form and [2].
Given the response-variable dimensionality, cointegrating rank, and short-run
polynomial degree, all coefficient matrices and innovation-distribution parameters are
unknown and estimable unless you specify their values by using name-value pair argument
syntax. To choose which Johansen form is suitable for your data, then estimate a model
containing all or partially unknown parameter values given the data, use estimate. To
work with an estimated or fully specified vecm model object, pass it to
an object function.
Alternatively, you can create and work with vecm model objects
interactively by using Econometric
Modeler.
Creation
Description
Mdl = vecm(numseries,rank,numlags)numlags) model composed of numseries time series containing rank cointegrating relations. The maximum nonzero lag in the short-run polynomial is numlags. All lags and the error-correction term have numseries-by-numseries coefficient matrices composed of NaN values.
This shorthand syntax allows for easy model template creation in which you specify the model dimensions explicitly. The model template is suited for unrestricted parameter estimation, that is, estimation without any parameter equality constraints. After you create a model, you can alter property values using dot notation.
Mdl = vecm(Name,Value)'Lags',[1 4],'ShortRun',ShortRun specifies the two short-run coefficient matrices in ShortRun at lags 1 and 4.
This longhand syntax allows for creating more flexible models. However, vecm must be able to infer the number of series (NumSeries) and cointegrating rank (Rank) from the specified name-value pair arguments. Name-value pair arguments and property values that correspond to the number of time series and cointegrating rank must be consistent with each other.
Input Arguments
The shorthand syntax provides an easy way for you to create model templates that are suitable for unrestricted parameter estimation. For example, to create a VEC(2) model composed of three response series containing one cointegrating relation and unknown parameter values, enter:
Mdl = vecm(3,1,2);
numseries — Number of time series m
1 (default) | positive integer
Number of time series m, specified as a positive integer. numseries specifies the dimensionality of the multivariate response variable yt and innovation εt.
numseries sets the NumSeries property.
Data Types: double
rank — Number of cointegrating relations
nonnegative integer
Number of cointegrating relations, specified as a nonnegative integer. The adjustment and cointegration matrices in the model have rank linearly independent columns, and are numseries-by-rank matrices composed of NaN values.
Data Types: double
numlags — Number of first differences of responses
nonnegative integer
Number of first differences of responses to include in the short-run polynomial of the VEC(p – 1) model, specified as a nonnegative integer. That is, numlags = p – 1. Consequently, numlags specifies the number of short-run terms associated with the corresponding VAR(p) model.
All lags have numseries-by-numseries short-run coefficient matrices composed of NaN values.
Data Types: double
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
The longhand syntax
enables you to create models in which some or all coefficients are known. During estimation,
estimate imposes equality constraints on any known parameters. Specify enough information for vecm to infer
the number of response series and the cointegrating rank.
Example: 'Adjustment',nan(3,2),'Lags',[4 8] specifies a
three-dimensional VEC(8) model with two cointegrating relations and nonzero
short-run coefficient matrices at lags 4 and
8.
Lags — Short-run polynomial lags
1:(P-1) (default) | numeric vector of unique positive integers
Short-run polynomial lags, specified as the comma-separated pair
consisting of 'Lags' and a numeric vector
containing at most P – 1 elements of unique
positive integers.
The matrix
ShortRun{ is the
coefficient of lag
j}Lags(.j)
Example: 'Lags',[1 4]
Data Types: double
Properties
You can set writable property values when you create the model object by using name-value argument syntax, or after you create the model object by using dot notation. For example, to create a VEC(1) model in the H1 Johansen form suitable for simulation, and composed of two response series of cointegrating rank one and no overall time trend term, enter:
Mdl = vecm('Constant',[0; 0.01],'Adjustment',[-0.1; 0.15],...
'Cointegration',[1; -4],'ShortRun',{[0.3 -0.15 ; 0.1 -0.3]},...
'Covariance',eye(2));
Mdl.Trend = 0;NumSeries — Number of time series m
positive integer
This property is read-only.
Number of time series m, specified as a positive integer. NumSeries specifies the dimensionality of the multivariate response variable yt and innovation εt.
Data Types: double
Rank — Number of cointegrating relations
nonnegative integer
This property is read-only.
Number of cointegrating relations, specified as a nonnegative integer. The adjustment and cointegration matrices in the model have Rank linearly independent columns and are NumSeries-by-Rank matrices.
Data Types: double
P — Corresponding VAR model order
nonnegative integer
This property is read-only.
Corresponding VAR model order, specified as a nonnegative integer. P – 1 is the maximum lag in the short-run polynomial that has a nonzero coefficient matrix. Lags in the short-run polynomial that have degree less than P – 1 can have coefficient matrices composed entirely of zeros.
P specifies the number of presample observations required to initialize the model.
Data Types: double
Description — Model description
string scalar | character vector
Model description, specified as a string scalar or character vector. vecm stores the value as a string scalar. The default value describes the parametric form of the model, for example
"2-Dimensional Rank = 1 VEC(1) Model".
Example: 'Description','Model 1'
Data Types: string | char
SeriesNames — Response series names
string vector | cell array of character vectors
Response series names, specified as a NumSeries length string vector. The
default is ['Y1' 'Y2' ...
'Y.NumSeries']
Example: 'SeriesNames',{'CPI' 'Unemployment'}
Data Types: string
Constant — Overall model constant
NaN(NumSeries,1) (default) | numeric vector
Overall model constant (c), specified as a NumSeries-by-1 numeric vector.
The value of Constant, and whether estimate supports equality constraints on it during estimation, depend on the Johansen form of the VEC model.
Example: 'Constant',[1; 2]
Data Types: double
Trend — Overall linear time trend
nan(NumSeries,1) (default) | numeric vector
Overall linear time trend (d), specified as a NumSeries-by-1 numeric vector.
The value of Trend, and whether estimate supports equality constraints on it during estimation, depend on the Johansen form of the VEC model.
Example: 'Trend',[0.1; 0.2]
Data Types: double
Adjustment — Cointegration adjustment speeds
NaN(NumSeries,Rank) (default) | numeric matrix
Cointegration adjustment speeds (A), specified as a NumSeries-by-Rank numeric matrix.
If you specify a matrix of known values, then all columns must be linearly independent (that is, Adjustment must be a matrix of full column rank).
For estimation, you can impose equality constraints on the cointegration adjustment speeds by supplying a matrix composed entirely of numeric values or a mixture of numeric and missing (NaN) values.
If Rank = 0, then Adjustment is an empty NumSeries-by-0 vector.
For more details on specifying Adjustment, see Algorithms.
Example: 'Adjustment',NaN(2,1)
Data Types: double
Cointegration — Cointegration matrix
NaN(NumSeries,Rank) (default) | numeric matrix
Cointegration matrix (B), specified as a NumSeries-by-Rank numeric matrix.
If you specify a matrix of known values, then all columns must be linearly independent (that is, Cointegration must be a matrix of full column rank).
Cointegration cannot contain a mixture of missing (NaN) values and numeric values. Supported equality constraints on the cointegration matrix during estimation depend on the Johansen form of the VEC model.
If Rank = 0, then Cointegration is an empty NumSeries-by-0 vector.
For more details on specifying Cointegration, see Algorithms.
Example: 'Cointegration',NaN(2,1)
Data Types: double
Impact — Impact matrix
numeric matrix
Impact, or long-run level, matrix (Π), specified as a NumSeries-by-NumSeries numeric matrix. The rank of Impact must be Rank.
For estimation of full-rank models (Rank = NumSeries), you can impose equality constraints on the impact matrix by supplying a matrix containing a mixture of numeric and missing values (NaN).
If 1 ≤ Rank ≤ NumSeries – 1, then the default value is Adjustment*Cointegration'.
If Rank = 0, then Impact is a matrix of zeros. Consequently, the model does not have an error-correction term.
For more details on specifying Impact, see Algorithms.
Example: 'Impact',[0.5 0.25 0; 0.3 0.15 0; 0 0 0.9]
Data Types: double
CointegrationConstant — Constant in cointegrating relations
NaN(Rank,1) (default) | numeric vector
Constant (intercept) in the cointegrating relations (c0), specified as a Rank-by-1 numeric vector. You can set CointegrationConstant only by using dot notation after you create the model.
CointegrationConstant cannot contain a mixture of missing (NaN) values and numeric values. Supported equality constraints on the cointegration constant vector during estimation depend on the Johansen form of the VEC model.
If Rank = 0, then CointegrationConstant is a 0-by-1 vector of zeros.
Example: Mdl.CointegrationConstant = [1; 0]
Data Types: double
CointegrationTrend — Time trend in cointegrating relations
NaN(Rank,1) (default) | numeric vector
Time trend in the cointegrating relations (d0), specified as a Rank-by-1 numeric vector. You can set CointegrationTrend only by using dot notation after you create the model.
CointegrationTrend cannot contain a mixture of missing (NaN) values and numeric values. Supported equality constraints on the cointegration linear trend vector during estimation depend on the Johansen form of the VEC model.
If Rank = 0, then CointegrationTrend is a 0-by-1 vector of zeros.
Example: Mdl.CointegrationTrend = [0; 0.5]
Data Types: double
ShortRun — Short-run coefficient matrices
cell vector of numeric matrices
Short-run coefficient matrices associated with the lagged response differences, specified as a cell vector of NumSeries-by-NumSeries numeric matrices.
Specify coefficient signs corresponding to those coefficients in the VEC model expressed in difference-equation notation. The property P is numel(ShortRun) + 1.
If you set the
'Lags'name-value pair argument toLags, the following conditions apply.The lengths of
ShortRunandLagsmust be equal.ShortRun{is the coefficient matrix of lagj}Lags(.j)By default,
ShortRunis anumel(Lags)-by-1 cell vector of matrices composed ofNaNvalues.
Otherwise, the following conditions apply.
ShortRun{is the coefficient matrix of lagj}j.By default,
ShortRunis a (P– 1)-by-1 cell vector of matrices composed ofNaNvalues.
MATLAB assumes that the coefficient of the current, differenced response (Δyt) is the identity matrix. Therefore, exclude this coefficient from ShortRun.
Example: 'ShortRun',{[0.5 -0.1; 0.1 0.2]}
Data Types: cell
Beta — Regression coefficient matrix
NumSeries-by-0 empty matrix (default) | numeric matrix
Regression coefficient matrix associated with the predictor variables, specified as a NumSeries-by-NumPreds numeric matrix. NumPreds is the number of predictor variables, that is, the number of columns in the predictor data.
Beta( contains the regression coefficients
for each predictor in the equation of response
yj,:)j,t.
Beta(:, contains the regression
coefficient in each response equation for predictor
xk. By default, all predictor variables
are in the regression component of all response equations. You can exclude certain
predictors from certain equations by specifying equality constraints to 0.k)
Example: In a model that includes 3 responses and 4 predictor variables, to exclude the
second predictor from the third equation and leave the others unrestricted, specify
[NaN NaN NaN NaN; NaN NaN NaN NaN; NaN 0 NaN NaN].
The default value specifies no regression coefficient in the model. However, if you specify
predictor data when you estimate the model using estimate, then
MATLAB sets Beta to an appropriately sized matrix of
NaN values.
Example: 'Beta',[2 3 -1 2; 0.5 -1 -6 0.1]
Data Types: double
Covariance — Innovations covariance matrix
NaN(NumSeries) (default) | numeric, positive definite matrix
Innovations covariance matrix of the NumSeries innovations at each time t = 1,...,T, specified as a NumSeries-by-NumSeries numeric, positive definite matrix.
Example: 'Covariance',eye(2)
Data Types: double
Note
NaN-valued elements in properties indicate unknown, estimable parameters. Specified elements indicate equality constraints on parameters in model estimation. The innovations covariance matrix Covariance cannot contain a mix of NaN values and real numbers; you must fully specify the covariance or it must be completely unknown (NaN(NumSeries)).
Object Functions
estimate | Fit vector error-correction (VEC) model to data |
fevd | Generate vector error-correction (VEC) model forecast error variance decomposition (FEVD) |
filter | Filter disturbances through vector error-correction (VEC) model |
forecast | Forecast vector error-correction (VEC) model responses |
infer | Infer vector error-correction (VEC) model innovations |
irf | Generate vector error-correction (VEC) model impulse responses |
simulate | Monte Carlo simulation of vector error-correction (VEC) model |
summarize | Display estimation results of vector error-correction (VEC) model |
varm | Convert vector error-correction (VEC) model to vector autoregression (VAR) model |
Examples
Prepare VEC Model Template for Parameter Estimation
Suppose that a VEC model with cointegrating rank of 4 and a short-run polynomial of degree 2 is appropriate for modeling the behavior of seven hypothetical macroeconometric time series.
Create a VEC(7,4,2) model using the shorthand syntax.
Mdl = vecm(7,4,2)
Mdl =
vecm with properties:
Description: "7-Dimensional Rank = 4 VEC(2) Model with Linear Time Trend"
SeriesNames: "Y1" "Y2" "Y3" ... and 4 more
NumSeries: 7
Rank: 4
P: 3
Constant: [7×1 vector of NaNs]
Adjustment: [7×4 matrix of NaNs]
Cointegration: [7×4 matrix of NaNs]
Impact: [7×7 matrix of NaNs]
CointegrationConstant: [4×1 vector of NaNs]
CointegrationTrend: [4×1 vector of NaNs]
ShortRun: {7×7 matrices of NaNs} at lags [1 2]
Trend: [7×1 vector of NaNs]
Beta: [7×0 matrix]
Covariance: [7×7 matrix of NaNs]
Mdl is a vecm model object that serves as a template for parameter estimation. MATLAB® considers the NaN values as unknown parameter values to be estimated. For example, the Adjustment property is a 7-by-4 matrix of NaN values. Therefore, the adjustment speeds are active model parameters to be estimated.
By default, MATLAB® includes overall and cointegrating linear time trend terms in the model. You can create a VEC model in H1 Johansen form by removing the time trend terms, that is, by setting the Trend property to 0 using dot notation.
Mdl.Trend = 0
Mdl =
vecm with properties:
Description: "7-Dimensional Rank = 4 VEC(2) Model"
SeriesNames: "Y1" "Y2" "Y3" ... and 4 more
NumSeries: 7
Rank: 4
P: 3
Constant: [7×1 vector of NaNs]
Adjustment: [7×4 matrix of NaNs]
Cointegration: [7×4 matrix of NaNs]
Impact: [7×7 matrix of NaNs]
CointegrationConstant: [4×1 vector of NaNs]
CointegrationTrend: [4×1 vector of NaNs]
ShortRun: {7×7 matrices of NaNs} at lags [1 2]
Trend: [7×1 vector of zeros]
Beta: [7×0 matrix]
Covariance: [7×7 matrix of NaNs]
MATLAB® expands Trend to the appropriate length, a 7-by-1 vector of zeros.
Specify All Parameter Values of VEC Model
Consider this VEC(1) model for three hypothetical response series.
The innovations are multivariate Gaussian with a mean of 0 and the covariance matrix
Create variables for the parameter values.
Adjustment = [-0.3 0.3; -0.2 0.1; -1 0];
Cointegration = [0.1 -0.7; -0.2 0.5; 0.2 0.2];
ShortRun = {[0. 0.1 0.2; 0.2 -0.2 0; 0.7 -0.2 0.3]};
Constant = [-1; -3; -30];
Trend = [0; 0; 0];
Covariance = [1.3 0.4 1.6; 0.4 0.6 0.7; 1.6 0.7 5];Create a vecm model object representing the VEC(1) model using the appropriate name-value pair arguments.
Mdl = vecm('Adjustment',Adjustment,'Cointegration',Cointegration,... 'Constant',Constant,'ShortRun',ShortRun,'Trend',Trend,... 'Covariance',Covariance)
Mdl =
vecm with properties:
Description: "3-Dimensional Rank = 2 VEC(1) Model"
SeriesNames: "Y1" "Y2" "Y3"
NumSeries: 3
Rank: 2
P: 2
Constant: [-1 -3 -30]'
Adjustment: [3×2 matrix]
Cointegration: [3×2 matrix]
Impact: [3×3 matrix]
CointegrationConstant: [2×1 vector of NaNs]
CointegrationTrend: [2×1 vector of NaNs]
ShortRun: {3×3 matrix} at lag [1]
Trend: [3×1 vector of zeros]
Beta: [3×0 matrix]
Covariance: [3×3 matrix]
Mdl is, effectively, a fully specified vecm model object. That is, the cointegration constant and linear trend are unknown. However, they are not needed for simulating observations or forecasting, given that the overall constant and trend parameters are known.
By default, vecm attributes the short-run coefficient to the first lag in the short-run polynomial. Consider another VEC model that attributes the short-run coefficient matrix ShortRun to the fourth lag term, specifies a matrix of zeros for the first lag coefficient, and treats all else as being equal to Mdl. Create this VEC(4) model.
Mdl.ShortRun(4) = ShortRun;
Mdl.ShortRun(1) = {0}Mdl =
vecm with properties:
Description: "3-Dimensional Rank = 2 VEC(4) Model"
SeriesNames: "Y1" "Y2" "Y3"
NumSeries: 3
Rank: 2
P: 5
Constant: [-1 -3 -30]'
Adjustment: [3×2 matrix]
Cointegration: [3×2 matrix]
Impact: [3×3 matrix]
CointegrationConstant: [2×1 vector of NaNs]
CointegrationTrend: [2×1 vector of NaNs]
ShortRun: {3×3 matrix} at lag [4]
Trend: [3×1 vector of zeros]
Beta: [3×0 matrix]
Covariance: [3×3 matrix]
Alternatively, you can create another model object using vecm and the same syntax as for Mdl, but additionally specify 'Lags',4.
Fit VEC(1) Model to Matrix of Response Data
Fit a VEC(1) model to seven macroeconomic series. Supply the response data as a numeric matrix.
Consider a VEC model for the following macroeconomic series:
Gross domestic product (GDP)
GDP implicit price deflator
Paid compensation of employees
Nonfarm business sector hours of all persons
Effective federal funds rate
Personal consumption expenditures
Gross private domestic investment
Suppose that a cointegrating rank of 4 and one short-run term are appropriate, that is, consider a VEC(1) model.
Load the Data_USEconVECModel data set.
load Data_USEconVECModelFor more information on the data set and variables, enter Description at the command line.
Determine whether the data needs to be preprocessed by plotting the series on separate plots.
figure tiledlayout(2,2) nexttile plot(FRED.Time,FRED.GDP); title("Gross Domestic Product"); ylabel("Index"); xlabel("Date"); nexttile plot(FRED.Time,FRED.GDPDEF); title("GDP Deflator"); ylabel("Index"); xlabel("Date"); nexttile plot(FRED.Time,FRED.COE); title("Paid Compensation of Employees"); ylabel("Billions of $"); xlabel("Date"); nexttile plot(FRED.Time,FRED.HOANBS); title("Nonfarm Business Sector Hours"); ylabel("Index"); xlabel("Date");
figure tiledlayout(2,2) nexttile plot(FRED.Time,FRED.FEDFUNDS) title("Federal Funds Rate") ylabel("Percent") xlabel("Date") nexttile plot(FRED.Time,FRED.PCEC) title("Consumption Expenditures") ylabel("Billions of $") xlabel("Date") nexttile plot(FRED.Time,FRED.GPDI) title("Gross Private Domestic Investment") ylabel("Billions of $") xlabel("Date")
Stabilize all series, except the federal funds rate, by applying the log transform. Scale the resulting series by 100 so that all series are on the same scale.
FRED.GDP = 100*log(FRED.GDP); FRED.GDPDEF = 100*log(FRED.GDPDEF); FRED.COE = 100*log(FRED.COE); FRED.HOANBS = 100*log(FRED.HOANBS); FRED.PCEC = 100*log(FRED.PCEC); FRED.GPDI = 100*log(FRED.GPDI);
Create a VEC(1) model using the shorthand syntax. Specify the variable names.
Mdl = vecm(7,4,1); Mdl.SeriesNames = FRED.Properties.VariableNames
Mdl =
vecm with properties:
Description: "7-Dimensional Rank = 4 VEC(1) Model with Linear Time Trend"
SeriesNames: "GDP" "GDPDEF" "COE" ... and 4 more
NumSeries: 7
Rank: 4
P: 2
Constant: [7×1 vector of NaNs]
Adjustment: [7×4 matrix of NaNs]
Cointegration: [7×4 matrix of NaNs]
Impact: [7×7 matrix of NaNs]
CointegrationConstant: [4×1 vector of NaNs]
CointegrationTrend: [4×1 vector of NaNs]
ShortRun: {7×7 matrix of NaNs} at lag [1]
Trend: [7×1 vector of NaNs]
Beta: [7×0 matrix]
Covariance: [7×7 matrix of NaNs]
Mdl is a vecm model object. All properties containing NaN values correspond to parameters to be estimated given data.
Estimate the model using the entire data set and the default options.
EstMdl = estimate(Mdl,FRED.Variables)
EstMdl =
vecm with properties:
Description: "7-Dimensional Rank = 4 VEC(1) Model"
SeriesNames: "GDP" "GDPDEF" "COE" ... and 4 more
NumSeries: 7
Rank: 4
P: 2
Constant: [14.1329 8.77841 -7.20359 ... and 4 more]'
Adjustment: [7×4 matrix]
Cointegration: [7×4 matrix]
Impact: [7×7 matrix]
CointegrationConstant: [-28.6082 109.555 -77.0912 ... and 1 more]'
CointegrationTrend: [4×1 vector of zeros]
ShortRun: {7×7 matrix} at lag [1]
Trend: [7×1 vector of zeros]
Beta: [7×0 matrix]
Covariance: [7×7 matrix]
EstMdl is an estimated vecm model object. It is fully specified because all parameters have known values. By default, estimate imposes the constraints of the H1 Johansen VEC model form by removing the cointegrating trend and linear trend terms from the model. Parameter exclusion from estimation is equivalent to imposing equality constraints to zero.
Display a short summary from the estimation.
results = summarize(EstMdl)
results = struct with fields:
Description: "7-Dimensional Rank = 4 VEC(1) Model"
Model: "H1"
SampleSize: 238
NumEstimatedParameters: 112
LogLikelihood: -1.4939e+03
AIC: 3.2118e+03
BIC: 3.6007e+03
Table: [133x4 table]
Covariance: [7x7 double]
Correlation: [7x7 double]
The Table field of results is a table of parameter estimates and corresponding statistics.
Forecast Responses from VEC Model
This example follows from Fit VEC(1) Model to Matrix of Response Data.
Create and estimate the VEC(1) model. Treat the last ten periods as the forecast horizon.
load Data_USEconVECModel
FRED.GDP = 100*log(FRED.GDP);
FRED.GDPDEF = 100*log(FRED.GDPDEF);
FRED.COE = 100*log(FRED.COE);
FRED.HOANBS = 100*log(FRED.HOANBS);
FRED.PCEC = 100*log(FRED.PCEC);
FRED.GPDI = 100*log(FRED.GPDI);
Mdl = vecm(7,4,1)Mdl =
vecm with properties:
Description: "7-Dimensional Rank = 4 VEC(1) Model with Linear Time Trend"
SeriesNames: "Y1" "Y2" "Y3" ... and 4 more
NumSeries: 7
Rank: 4
P: 2
Constant: [7×1 vector of NaNs]
Adjustment: [7×4 matrix of NaNs]
Cointegration: [7×4 matrix of NaNs]
Impact: [7×7 matrix of NaNs]
CointegrationConstant: [4×1 vector of NaNs]
CointegrationTrend: [4×1 vector of NaNs]
ShortRun: {7×7 matrix of NaNs} at lag [1]
Trend: [7×1 vector of NaNs]
Beta: [7×0 matrix]
Covariance: [7×7 matrix of NaNs]
Y = FRED{1:(end - 10),:};
EstMdl = estimate(Mdl,Y)EstMdl =
vecm with properties:
Description: "7-Dimensional Rank = 4 VEC(1) Model"
SeriesNames: "Y1" "Y2" "Y3" ... and 4 more
NumSeries: 7
Rank: 4
P: 2
Constant: [14.5023 8.46791 -7.08266 ... and 4 more]'
Adjustment: [7×4 matrix]
Cointegration: [7×4 matrix]
Impact: [7×7 matrix]
CointegrationConstant: [-32.8433 -101.126 -84.2373 ... and 1 more]'
CointegrationTrend: [4×1 vector of zeros]
ShortRun: {7×7 matrix} at lag [1]
Trend: [7×1 vector of zeros]
Beta: [7×0 matrix]
Covariance: [7×7 matrix]
Forecast 10 responses using the estimated model and in-sample data as presample observations.
YF = forecast(EstMdl,10,Y);
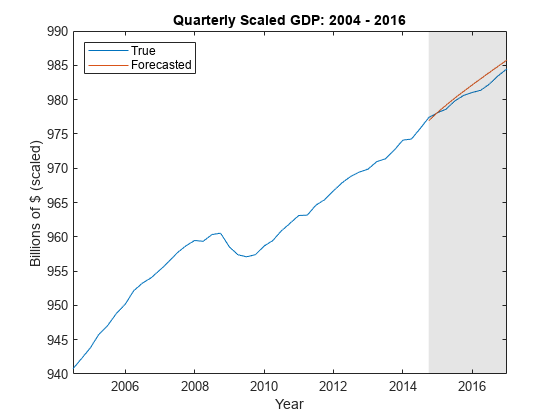
On separate plots, plot part of the GDP and GPDI series with their forecasted values.
figure; plot(FRED.Time(end - 50:end),FRED.GDP(end - 50:end)); hold on plot(FRED.Time((end - 9):end),YF(:,1)) h = gca; fill(FRED.Time([end - 9 end end end - 9]),h.YLim([1,1,2,2]),'k',... 'FaceAlpha',0.1,'EdgeColor','none'); legend('True','Forecasted','Location','NW') title('Quarterly Scaled GDP: 2004 - 2016'); ylabel('Billions of $ (scaled)'); xlabel('Year'); hold off
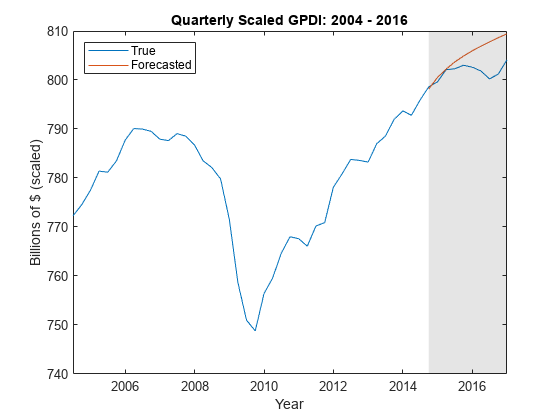
figure; plot(FRED.Time(end - 50:end),FRED.GPDI(end - 50:end)); hold on plot(FRED.Time((end - 9):end),YF(:,7)) h = gca; fill(FRED.Time([end - 9 end end end - 9]),h.YLim([1,1,2,2]),'k',... 'FaceAlpha',0.1,'EdgeColor','none'); legend('True','Forecasted','Location','NW') title('Quarterly Scaled GPDI: 2004 - 2016'); ylabel('Billions of $ (scaled)'); xlabel('Year'); hold off
More About
Vector Error-Correction Model
A vector error-correction (VEC) model is a
multivariate, stochastic time series model consisting of a system of m =
numseries equations of m distinct, differenced
response variables. Equations in the system can include an error-correction
term, which is a linear function of the responses in levels used to
stabilize the system. The cointegrating rank
r is the number of cointegrating relations that
exist in the system.
Each response equation can include an autoregressive polynomial composed of first differences of the response series (short-run polynomial of degree p – 1), a constant, a time trend, exogenous predictor variables, and a constant and time trend in the error-correction term.
A VEC(p – 1) model in difference-equation notation and in reduced form can be expressed in two ways:
This equation is the component form of a VEC model, where the cointegration adjustment speeds and cointegration matrix are explicit, whereas the impact matrix is implied.
The cointegrating relations are B'yt – 1 + c0 + d0t and the error-correction term is A(B'yt – 1 + c0 + d0t).
This equation is the impact form of a VEC model, where the impact matrix is explicit, whereas the cointegration adjustment speeds and cointegration matrix are implied.
In the equations:
yt is an m-by-1 vector of values corresponding to m response variables at time t, where t = 1,...,T.
Δyt = yt – yt – 1. The structural coefficient is the identity matrix.
r is the number of cointegrating relations and, in general, 0 < r < m.
A is an m-by-r matrix of adjustment speeds.
B is an m-by-r cointegration matrix.
Π is an m-by-m impact matrix with a rank of r.
c0 is an r-by-1 vector of constants (intercepts) in the cointegrating relations.
d0 is an r-by-1 vector of linear time trends in the cointegrating relations.
c1 is an m-by-1 vector of constants (deterministic linear trends in yt).
d1 is an m-by-1 vector of linear time-trend values (deterministic quadratic trends in yt).
c = Ac0 + c1 and is the overall constant.
d = Ad0 + d1 and is the overall time-trend coefficient.
Φj is an m-by-m matrix of short-run coefficients, where j = 1,...,p – 1 and Φp – 1 is not a matrix containing only zeros.
xt is a k-by-1 vector of values corresponding to k exogenous predictor variables.
β is an m-by-k matrix of regression coefficients.
εt is an m-by-1 vector of random Gaussian innovations, each with a mean of 0 and collectively an m-by-m covariance matrix Σ. For t ≠ s, εt and εs are independent.
Condensed and in lag operator notation, the system is
where , I is the m-by-m identity matrix, and Lyt = yt – 1.
If m = r, then the VEC model is a stable VAR(p) model in the levels of the responses. If r = 0, then the error-correction term is a matrix of zeros, and the VEC(p – 1) model is a stable VAR(p – 1) model in the first differences of the responses.
Johansen Form
The Johansen forms of a VEC Model differ with respect to the presence of deterministic terms. As detailed in [2], the estimation procedure differs among the forms. Consequently, allowable equality constraints on the deterministic terms during estimation differ among forms. For more details, see The Role of Deterministic Terms.
This table describes the five Johansen forms and supported equality constraints.
| Form | Error-Correction Term | Deterministic Coefficients | Equality Constraints |
|---|---|---|---|
| H2 | AB´yt − 1 | c = 0 (Constant). d = 0 (Trend). c0 = 0 (CointegrationConstant). d0 = 0 (CointegrationTrend). | You can fully specify B. All deterministic coefficients are zero. |
| H1* | A(B´yt−1+c0) | c = Ac0. d = 0. d0 = 0. | If you fully specify either B or c0, then you must fully specify the other. MATLAB derives the value of c from c0 and A. All deterministic trends are zero. |
| H1 | A(B´yt−1 + c0) + c1 | c = Ac0 + c1. d = 0. d0 = 0. | You can fully specify B. You can specify a mixture of MATLAB derives the value of c0 from c and A. All deterministic trends are zero. |
| H* | A(B´yt−1 + c0 + d0t) + c1 | c = Ac0 + c1. d = Ad0. | If you fully specify either B or d0, then you must fully specify the other. You can specify a mixture of MATLAB derives the value of c0 from c and A. MATLAB derives the value of d from A and d0. |
| H | A(B´yt−1+c0+d0t)+c1+d1t | c = Ac0 + c1. d = A.d0 + d1. | You can fully specify B. You can specify a mixture of MATLAB derives the values of c0 and d0 from c, d, and A. |
Algorithms
VEC Model Forms
VEC models can take one of two forms: component form or impact form.
If you create a
vecmmodel object using the shorthand syntax, and then assign a value to at least one of these properties–Adjustment,Cointegration,CointegrationConstant, orCointegrationTrend–before assigning a value to theImpactproperty, then the model takes the component form.If you create a
vecmmodel object using the longhand syntax by assigning a value to either theAdjustmentorCointegrationproperty (or both), but leave theImpactproperty unspecified, then the model the component form.If
1≤Rank≤NumSeries–1, as is the case for most VEC model analyses, then it can be more convenient to work with the model in component form rather than impact form.The Impact property is read-only and depends on the values of the
CointegrationandAdjustmentproperties. Specifically,Impact=Adjustment*Cointegration'.During estimation, MATLAB fits the VEC model to the data in two steps. First, it estimates the cointegrating relations. Second, it constructs a VARX model from the differenced responses and short-run polynomial, includes an exogenous term for the estimated cointegrating relations, and then fits the VARX model to the differenced response data.
If you create a
vecmmodel object using the shorthand syntax, and then assign a value to theImpactproperty before assigning a value to any of these properties–Adjustment,Cointegration,CointegrationConstant, orCointegrationTrend–then the model takes the impact form.If you create a
vecmmodel object using the longhand syntax by assigning a value to theImpactproperty, but leave either theAdjustmentorCointegrationproperty (or both) unspecified, then the model takes the impact form.If the value of the Impact property is a full-rank matrix (
Rank=NumSeries), then it can be more convenient to work with the model in impact form rather than component form. The corresponding VEC model has no unit roots. Therefore, the model is a stable VAR(P) model. Because each individual response variable is stable, any linear combination of response variables is also stable.Because matrix factorizations are not necessarily unique, the values of the
CointegrationandAdjustmentproperties are unknown. Therefore, after you pass thevecmmodel object toestimate, MATLAB sets theCointegrationproperty to theNumSeries-by-NumSeriesidentity matrix and theAdjustmentproperty to the value ofImpactin the estimatedvecmmodel object.The
CointegrationandAdjustmentproperties are read-only and depend on the value ofImpact.During estimation, MATLAB fits the model in one step: it fits the equivalent VARX(
P) model to the differenced responses and includes yt – 1 as exogenous predictors in the regression component.
When using the longhand syntax to create a
vecmmodel object, if you assign a value to theImpactproperty and either theAdjustmentorCointegrationproperty (or both) simultaneously, then MATLAB uses the cointegration rankRankto determine the form of thevecmmodel object. Specifically, if 1 ≤Rank≤NumSeries–1, then the model object is in component form. Otherwise, the model object is in impact form.If the model is fully specified, then the form of the
vecmmodel object is irrelevant.
Deterministic Parameters
MATLAB does not store c1 and δ1, but you can compute them using Adjustment, Constant, CointegrationConstant, Trend, CointegrationTrend, and the corresponding Johansen form of the VEC model.
References
[1] Hamilton, James D. Time Series Analysis. Princeton, NJ: Princeton University Press, 1994.
[2] Johansen, S. Likelihood-Based Inference in Cointegrated Vector Autoregressive Models. Oxford: Oxford University Press, 1995.
[3] Juselius, K. The Cointegrated VAR Model. Oxford: Oxford University Press, 2006.
[4] Lütkepohl, H. New Introduction to Multiple Time Series Analysis. Berlin: Springer, 2005.
Version History
Introduced in R2017bR2019b: Equality constraints on innovations covariance matrix
If you specify a positive definite innovations covariance matrix for the
Covariance property, estimate treats your
specification as an equality constraint in model estimation.
See Also
Apps
Objects
Functions
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)