boxcox
Box-Cox transformation
Description
Examples
Transform a Data Series Contained in Vector of Data
Use boxcox to transform the data series contained in a vector of data into another set of data series with relatively normal distributions.
Load the SimulatedStock.mat data file.
load SimulatedStock.matTransform the nonnormally distributed filled data series TMW_CLOSE into a normally distributed one using Box-Cox transformation.
[Xbc, lambdabc] = boxcox(TMW_CLOSE)
Xbc = 1000×1
7.8756
7.8805
7.9173
7.8557
7.8245
7.7844
7.7811
7.8029
7.8015
7.7229
⋮
lambdabc = 0.2151
Compare the result of the TMW_CLOSE data series with a normal (Gaussian) probability distribution function and the nonnormally distributed TMW_CLOSE.
subplot(2, 1, 1); histogram(TMW_CLOSE); grid; title('Nonnormally Distributed Data'); subplot(2, 1, 2); histogram(Xbc); grid; title('Box-Cox Transformed Data');
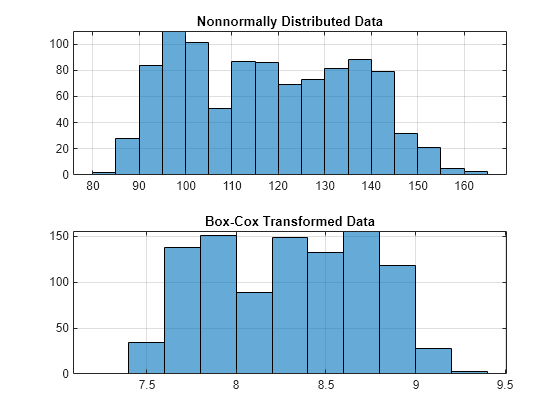
The bar chart on the top represents the probability distribution function of the data series, TMW_CLOSE, which is the original data series. The distribution is skewed toward the left (not normally distributed). The bar chart on the bottom is less skewed to the left. If you plot a Gaussian probability distribution function (PDF) with similar mean and standard deviation, the distribution of the transformed data is close to normal (Gaussian). When you examine the contents of the resulting object Xbc, you find an identical object to the original object TMW_CLOSE but the contents are the transformed data series.
Input Arguments
data — Data
positive column vector
Data, specified as a positive column vector.
Data Types: double
lambda — Lambda
numeric | structure
Lambda, specified as a scalar numeric or structure.
If the input data is a vector,
lambda is a scalar. If the input is a financial time
series object (tsobj), lambda is a
structure with fields similar to the components of the object. For example,
if tsobj contains series names Open
and Close, lambda has fields
lambda.Open and
lambda.Close.
Data Types: double | struct
Output Arguments
transdat — Data Box-Cox transformation
vector
Data Box-Cox transformation, returned as a vector.
lambda — Lambda transformation parameter
numeric
Lambda transformation parameter, returned as a numeric.
More About
Box Cox Transformation
boxcox transforms nonnormally distributed data
to a set of data that has approximately normal distribution. The Box-Cox
transformation is a family of power transformations.
If λ is not = 0, then
If λ is = 0, then
The logarithm is the natural logarithm (log base e). The algorithm calls for
finding the λ value that maximizes the Log-Likelihood Function (LLF). The search is
conducted using fminsearch.
Version History
Introduced before R2006aR2023a: fints support for tsobj input argument and transfts output argument are removed
The tsobj input argument that supports a
fints object is and the transfts output
argument are removed from boxcox.
See Also
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)