Portfolio Optimization Examples Using Financial Toolbox
Follow a sequence of examples that highlight features of the Portfolio object. Specifically, the examples use the Portfolio object to show how to set up mean-variance portfolio optimization problems that focus on the two-fund theorem, the impact of transaction costs and turnover constraints, how to obtain portfolios that maximize the Sharpe ratio, and how to set up two popular hedge-fund strategies — dollar-neutral and 130-30 portfolios.
Set up the Data
Every example works with moments for monthly total returns of a universe of 30 "blue-chip" stocks. Although derived from real data, these data are for illustrative purposes and are not meant to be representative of specific assets or of market performance. The data are contained in the file BlueChipStockMoments.mat with a list of asset identifiers in the variable AssetList, a mean and covariance of asset returns in the variables AssetMean and AssetCovar, and the mean and variance of cash and market returns in the variables CashMean, CashVar, MarketMean, and MarketVar. Since most of the analysis requires the use of the standard deviation of asset returns as the proxy for risk, cash, and market variances are converted into standard deviations.
load BlueChipStockMoments
mret = MarketMean;
mrsk = sqrt(MarketVar);
cret = CashMean;
crsk = sqrt(CashVar);Create a Portfolio Object
First create a "standard" Portfolio object with Portfolio to incorporate the list of assets, the risk-free rate, and the moments of asset returns into the object.
p = Portfolio('AssetList',AssetList,'RiskFreeRate',CashMean); p = setAssetMoments(p,AssetMean,AssetCovar);
To provide a basis for comparison, set up an equal-weight portfolio and make it the initial portfolio in the Portfolio object. Keep in mind that the hedged portfolios to be constructed later will require a different initial portfolio. Once the initial portfolio is created, the estimatePortMoments function estimates the mean and standard deviation of equal-weight portfolio returns.
p = setInitPort(p,1/p.NumAssets); [ersk,eret] = estimatePortMoments(p,p.InitPort);
A specialized "helper" function portfolioexamples_plot makes it possible to plot all results to be developed here. The first plot shows the distribution of individual assets according to their means and standard deviations of returns. In addition, the equal-weight, market, and cash portfolios are plotted on the same plot. Note that the portfolioexamples_plot function converts monthly total returns into annualized total returns.
clf; portfolioexamples_plot('Asset Risks and Returns', ... {'scatter', mrsk, mret, {'Market'}}, ... {'scatter', crsk, cret, {'Cash'}}, ... {'scatter', ersk, eret, {'Equal'}}, ... {'scatter', sqrt(diag(p.AssetCovar)), p.AssetMean, p.AssetList, '.r'});

Set up a Portfolio Optimization Problem
Set up a "standard" or default mean-variance portfolio optimization problem with the setDefaultConstraints function that requires fully-invested long-only portfolios (non-negative weights that must sum to 1). Given this initial problem, estimate the efficient frontier with the functions estimateFrontier and estimatePortMoments, where estimateFrontier estimates efficient portfolios and estimatePortMoments estimates risks and returns for portfolios. The next figure overlays the efficient frontier on the previous plot.
p = setDefaultConstraints(p); pwgt = estimateFrontier(p,20); [prsk,pret] = estimatePortMoments(p,pwgt); % Plot the efficient frontier. clf; portfolioexamples_plot('Efficient Frontier', ... {'line', prsk, pret}, ... {'scatter', [mrsk, crsk, ersk], [mret, cret, eret], {'Market', 'Cash', 'Equal'}}, ... {'scatter', sqrt(diag(p.AssetCovar)), p.AssetMean, p.AssetList, '.r'});

Illustrate the Tangent Line to the Efficient Frontier
Tobin's mutual fund theorem (Tobin 1958) says that the portfolio allocation problem is viewed as a decision to allocate between a riskless asset and a risky portfolio. In the mean-variance framework, cash serves as a proxy for a riskless asset and an efficient portfolio on the efficient frontier serves as the risky portfolio such that any allocation between cash and this portfolio dominates all other portfolios on the efficient frontier. This portfolio is called a tangency portfolio because it is located at the point on the efficient frontier where a tangent line that originates at the riskless asset touches the efficient frontier.
Given that the Portfolio object already has the risk-free rate, obtain the tangent line by creating a copy of the Portfolio object with a budget constraint that permits allocation between 0% and 100% in cash. Since the Portfolio object is a value object, it is easy to create a copy by assigning the output of either Portfolio or the "set" functions to a new instance of the Portfolio object. The plot shows the efficient frontier with Tobin's allocations that form the tangent line to the efficient frontier.
q = setBudget(p, 0, 1); qwgt = estimateFrontier(q,20); [qrsk,qret] = estimatePortMoments(q,qwgt); % Plot efficient frontier with tangent line (0 to 1 cash). clf; portfolioexamples_plot('Efficient Frontier with Tangent Line', ... {'line', prsk, pret}, ... {'line', qrsk, qret, [], [], 1}, ... {'scatter', [mrsk, crsk, ersk], [mret, cret, eret], {'Market', 'Cash', 'Equal'}}, ... {'scatter', sqrt(diag(p.AssetCovar)), p.AssetMean, p.AssetList, '.r'});

Note that cash actually has a small risk so that the tangent line does not pass through the cash asset.
Obtain Range of Risks and Returns
To obtain efficient portfolios with target values of either risk or return, it is necessary to obtain the range of risks and returns among all portfolios on the efficient frontier. This is accomplished with the estimateFrontierLimits function.
[rsk,ret] = estimatePortMoments(p,estimateFrontierLimits(p)); display(rsk)
rsk = 2×1
0.0348
0.0903
display(ret)
ret = 2×1
0.0094
0.0179
The range of monthly portfolio returns is between 0.9% and 1.8% and the range for portfolio risks is between 3.5% and 9.0%. In annualized terms, the range of portfolio returns is 11.2% to 21.5% and the range of portfolio risks is 12.1% to 31.3%.
Find a Portfolio with a Targeted Return and Targeted Risk
Given the range of risks and returns, it is possible to locate specific portfolios on the efficient frontier that have target values for return and risk using the functions estimateFrontierByReturn and estimateFrontierByRisk.
TargetReturn = 0.20; % Input target annualized return and risk here. TargetRisk = 0.15; % Obtain portfolios with targeted return and risk. awgt = estimateFrontierByReturn(p,TargetReturn/12); [arsk,aret] = estimatePortMoments(p,awgt); bwgt = estimateFrontierByRisk(p,TargetRisk/sqrt(12)); [brsk,bret] = estimatePortMoments(p,bwgt); % Plot efficient frontier with targeted portfolios. clf; portfolioexamples_plot('Efficient Frontier with Targeted Portfolios', ... {'line', prsk, pret}, ... {'scatter', [mrsk, crsk, ersk], [mret, cret, eret], {'Market', 'Cash', 'Equal'}}, ... {'scatter', arsk, aret, {sprintf('%g%% Return',100*TargetReturn)}}, ... {'scatter', brsk, bret, {sprintf('%g%% Risk',100*TargetRisk)}}, ... {'scatter', sqrt(diag(p.AssetCovar)), p.AssetMean, p.AssetList, '.r'});

To see what these targeted portfolios look like, use the dataset object to set up "blotters" that contain the portfolio weights and asset names (which are obtained from the Portfolio object).
aBlotter = dataset({100*awgt(awgt > 0),'Weight'}, 'obsnames', p.AssetList(awgt > 0));
displayPortfolio(sprintf('Portfolio with %g%% Target Return', 100*TargetReturn), aBlotter, false);Portfolio with 20% Target Return
Weight
CAT 1.1445
INTC 0.17452
MO 9.6521
MSFT 0.85862
UTX 56.918
WMT 31.253
bBlotter = dataset({100*bwgt(bwgt > 0),'Weight'}, 'obsnames', p.AssetList(bwgt > 0));
displayPortfolio(sprintf('Portfolio with %g%% Target Risk', 100*TargetRisk), bBlotter, false);Portfolio with 15% Target Risk
Weight
AA 1.8565e-21
AIG 5.962e-21
AXP 1.1063e-20
CAT 1.9038e-20
DD 3.2518e-21
DIS 1.6003e-20
GE 9.607e-22
HPQ 2.4156e-21
IBM 5.8501e-21
INTC 2.2585
JNJ 9.2162
MMM 16.603
MO 15.388
MSFT 4.4467
PFE 3.4596e-21
PG 4.086
UTX 10.281
WMT 25.031
XOM 12.69
Transactions Costs
The Portfolio object makes it possible to account for transaction costs as part of the optimization problem. Although individual costs can be set for each asset, use the scalar expansion features of the Portfolio object's functions to set up uniform transaction costs across all assets and compare efficient frontiers with gross versus net portfolio returns.
BuyCost = 0.0020; SellCost = 0.0020; q = setCosts(p,BuyCost,SellCost); qwgt = estimateFrontier(q,20); [qrsk,qret] = estimatePortMoments(q,qwgt); % Plot efficient frontiers with gross and net returns. clf; portfolioexamples_plot('Efficient Frontier with and without Transaction Costs', ... {'line', prsk, pret, {'Gross'}, ':b'}, ... {'line', qrsk, qret, {'Net'}}, ... {'scatter', [mrsk, crsk, ersk], [mret, cret, eret], {'Market', 'Cash', 'Equal'}}, ... {'scatter', sqrt(diag(p.AssetCovar)), p.AssetMean, p.AssetList, '.r'});

Turnover Constraint
In addition to transaction costs, the Portfolio object can handle turnover constraints. The following example demonstrates that a turnover constraint produces an efficient frontier in the neighborhood of an initial portfolio that may restrict trading. Moreover, the introduction of a turnover constraint often implies that multiple trades may be necessary to shift from an initial portfolio to an unconstrained efficient frontier. Consequently, the turnover constraint introduces a form of time diversification that can spread trades out over multiple time periods. In this example, note that the sum of purchases and sales from the estimateFrontier function confirms that the turnover constraint is satisfied.
BuyCost = 0.0020; SellCost = 0.0020; Turnover = 0.2; q = setCosts(p, BuyCost,SellCost); q = setTurnover(q,Turnover); [qwgt,qbuy,qsell] = estimateFrontier(q,20); [qrsk,qret] = estimatePortMoments(q,qwgt); % Plot efficient frontier with turnover constraint. clf; portfolioexamples_plot('Efficient Frontier with Turnover Constraint', ... {'line', prsk, pret, {'Unconstrained'}, ':b'}, ... {'line', qrsk, qret, {sprintf('%g%% Turnover', 100*Turnover)}}, ... {'scatter', [mrsk, crsk, ersk], [mret, cret, eret], {'Market', 'Cash', 'Equal'}}, ... {'scatter', sqrt(diag(p.AssetCovar)), p.AssetMean, p.AssetList, '.r'});

displaySumOfTransactions(Turnover, qbuy, qsell)
Sum of Purchases by Portfolio along Efficient Frontier (Max. Turnover 20%) 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 Sum of Sales by Portfolio along Efficient Frontier (Max. Turnover 20%) 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000 20.0000
Tracking-Error Constraint
The Portfolio object can handle tracking-error constraints, where tracking-error is the relative risk of a portfolio compared with a tracking portfolio. In this example, a sub-collection of nine assets forms an equally-weighted tracking portfolio. The goal is to find efficient portfolios with tracking errors that are within 5% of this tracking portfolio.
ii = [15, 16, 20, 21, 23, 25, 27, 29, 30]; % Indexes of assets to include in the tracking portfolio. TrackingError = 0.05/sqrt(12); TrackingPort = zeros(30, 1); TrackingPort(ii) = 1; TrackingPort = (1/sum(TrackingPort))*TrackingPort; q = setTrackingError(p,TrackingError,TrackingPort); qwgt = estimateFrontier(q,20); [qrsk,qret] = estimatePortMoments(q,qwgt); [trsk,tret] = estimatePortMoments(q,TrackingPort); % Plot the efficient frontier with tracking-error constraint. clf; portfolioexamples_plot('Efficient Frontier with 5% Tracking-Error Constraint', ... {'line', prsk, pret, {'Unconstrained'}, ':b'}, ... {'line', qrsk, qret, {'Tracking'}}, ... {'scatter', [mrsk, crsk], [mret, cret], {'Market', 'Cash'}}, ... {'scatter', trsk, tret, {'Tracking'}, 'r'});

Combined Turnover and Tracking-Error Constraints
This example illustrates the interactions that can occur with combined constraints. In this case, both a turnover constraint relative to an initial equal-weight portfolio and a tracking-error constraint relative to a tracking portfolio must be satisfied. The turnover constraint has a maximum of 30% turnover and the tracking-error constraint has a maximum of 5% tracking error. Note that the turnover to get from the initial portfolio to the tracking portfolio is 70% so that an upper bound of 30% turnover means that the efficient frontier will lie somewhere between the initial portfolio and the tracking portfolio.
Turnover = 0.3; InitPort = (1/q.NumAssets)*ones(q.NumAssets, 1); ii = [15, 16, 20, 21, 23, 25, 27, 29, 30]; % Indexes of assets to include in tracking portfolio. TrackingError = 0.05/sqrt(12); TrackingPort = zeros(30, 1); TrackingPort(ii) = 1; TrackingPort = (1/sum(TrackingPort))*TrackingPort; q = setTurnover(q,Turnover,InitPort); qwgt = estimateFrontier(q,20); [qrsk,qret] = estimatePortMoments(q,qwgt); [trsk,tret] = estimatePortMoments(q,TrackingPort); [ersk,eret] = estimatePortMoments(q,InitPort); % Plot the efficient frontier with combined turnover and tracking-error constraint. clf; portfolioexamples_plot('Efficient Frontier with Turnover and Tracking-Error Constraint', ... {'line', prsk, pret, {'Unconstrained'}, ':b'}, ... {'line', qrsk, qret, {'Turnover & Tracking'}}, ... {'scatter', [mrsk, crsk], [mret, cret], {'Market', 'Cash'}}, ... {'scatter', trsk, tret, {'Tracking'}, 'r'}, ... {'scatter', ersk, eret, {'Initial'}, 'b'});

Maximize the Sharpe Ratio
The Sharpe ratio (Sharpe 1966) is a measure of return-to-risk that plays an important role in portfolio analysis. Specifically, a portfolio that maximizes the Sharpe ratio is also the tangency portfolio on the efficient frontier from the mutual fund theorem. The maximum Sharpe ratio portfolio is located on the efficient frontier with the function estimateMaxSharpeRatio and the dataset object is used to list the assets in this portfolio.
p = setInitPort(p, 0); swgt = estimateMaxSharpeRatio(p); [srsk,sret] = estimatePortMoments(p,swgt); % Plot the efficient frontier with portfolio that attains maximum Sharpe ratio. clf; portfolioexamples_plot('Efficient Frontier with Maximum Sharpe Ratio Portfolio', ... {'line', prsk, pret}, ... {'scatter', srsk, sret, {'Sharpe'}}, ... {'scatter', [mrsk, crsk, ersk], [mret, cret, eret], {'Market', 'Cash', 'Equal'}}, ... {'scatter', sqrt(diag(p.AssetCovar)), p.AssetMean, p.AssetList, '.r'});

% Set up a dataset object that contains the portfolio that maximizes the Sharpe ratio. Blotter = dataset({100*swgt(swgt > 0),'Weight'}, 'obsnames', AssetList(swgt > 0)); displayPortfolio('Portfolio with Maximum Sharpe Ratio', Blotter, false);
Portfolio with Maximum Sharpe Ratio
Weight
AA 1.9673e-15
AIG 1.9059e-15
AXP 1.0567e-15
BA 5.6012e-16
C 2.0055e-15
CAT 2.9715e-15
DD 3.1346e-16
DIS 5.9556e-16
GE 5.6143e-15
GM 7.3245e-16
HD 2.0342e-11
HON 3.309e-16
HPQ 2.0307e-15
IBM 8.8744e-15
INTC 2.6638
JNJ 9.0044
JPM 5.4025e-16
KO 2.4602e-16
MCD 8.7471e-16
MMM 15.502
MO 13.996
MRK 3.2239e-16
MSFT 4.4777
PFE 7.3425e-16
PG 7.4588
SBC 3.8329e-16
UTX 6.0056
VZ 3.9079e-16
WMT 22.051
XOM 18.841
Confirm that Maximum Sharpe Ratio is a Maximum
The following plot demonstrates that this portfolio (which is located at the dot on the plots) indeed maximizes the Sharpe ratio among all portfolios on the efficient frontier.
psratio = (pret - p.RiskFreeRate) ./ prsk; ssratio = (sret - p.RiskFreeRate) / srsk; clf; subplot(2,1,1); plot(prsk, pret, 'LineWidth', 2); hold on scatter(srsk, sret, 'g', 'filled'); title('\bfEfficient Frontier'); xlabel('Portfolio Risk'); ylabel('Portfolio Return'); hold off subplot(2,1,2); plot(prsk, psratio, 'LineWidth', 2); hold on scatter(srsk, ssratio, 'g', 'filled'); title('\bfSharpe Ratio'); xlabel('Portfolio Risk'); ylabel('Sharpe Ratio'); hold off

Illustrate that Sharpe is the Tangent Portfolio
The next plot demonstrates that the portfolio that maximizes the Sharpe ratio is also a tangency portfolio (in this case, the budget constraint is opened up to permit between 0% and 100% in cash).
q = setBudget(p, 0, 1); qwgt = estimateFrontier(q,20); [qrsk,qret] = estimatePortMoments(q,qwgt); % Plot showing that the Sharpe ratio portfolio is the tangency portfolio. clf; portfolioexamples_plot('Efficient Frontier with Maximum Sharpe Ratio Portfolio', ... {'line', prsk, pret}, ... {'line', qrsk, qret, [], [], 1}, ... {'scatter', srsk, sret, {'Sharpe'}}, ... {'scatter', [mrsk, crsk, ersk], [mret, cret, eret], {'Market', 'Cash', 'Equal'}}, ... {'scatter', sqrt(diag(p.AssetCovar)), p.AssetMean, p.AssetList, '.r'});

Dollar-Neutral Hedge-Fund Structure
To illustrate how to use the portfolio optimization tools in hedge fund management, two popular strategies with dollar-neutral and 130-30 portfolios are examined. The dollar-neutral strategy invests equally in long and short positions such that the net portfolio position is 0. Such a portfolio is said to be "dollar-neutral."
To set up a dollar-neutral portfolio, start with the "standard" portfolio problem and set the maximum exposure in long and short positions in the variable Exposure. The bounds for individual asset weights are plus or minus Exposure. Since the net position must be dollar-neutral, the budget constraint is 0 and the initial portfolio must be 0. Finally, the one-way turnover constraints provide the necessary long and short restrictions to prevent "double-counting" of long and short positions. The blotter shows the portfolio weights for the dollar-neutral portfolio that maximizes the Sharpe ratio. The long and short positions are obtained from the buy and sell trades relative to the initial portfolio.
Exposure = 1; q = setBounds(p, -Exposure, Exposure); q = setBudget(q, 0, 0); q = setOneWayTurnover(q, Exposure, Exposure, 0); [qwgt,qlong,qshort] = estimateFrontier(q,20); [qrsk,qret] = estimatePortMoments(q,qwgt); [qswgt,qslong,qsshort] = estimateMaxSharpeRatio(q); [qsrsk,qsret] = estimatePortMoments(q,qswgt); % Plot the efficient frontier for a dollar-neutral fund structure with tangency portfolio. clf; portfolioexamples_plot('Efficient Frontier with Dollar-Neutral Portfolio', ... {'line', prsk, pret, {'Standard'}, 'b:'}, ... {'line', qrsk, qret, {'Dollar-Neutral'}, 'b'}, ... {'scatter', qsrsk, qsret, {'Sharpe'}}, ... {'scatter', [mrsk, crsk, ersk], [mret, cret, eret], {'Market', 'Cash', 'Equal'}}, ... {'scatter', sqrt(diag(p.AssetCovar)), p.AssetMean, p.AssetList, '.r'});

% Set up a dataset object that contains the portfolio that maximizes the Sharpe ratio. Blotter = dataset({100*qswgt(abs(qswgt) > 1.0e-4), 'Weight'}, ... {100*qslong(abs(qswgt) > 1.0e-4), 'Long'}, ... {100*qsshort(abs(qswgt) > 1.0e-4), 'Short'}, ... 'obsnames', AssetList(abs(qswgt) > 1.0e-4)); displayPortfolio('Dollar-Neutral Portfolio with Maximum Sharpe Ratio', Blotter, true, 'Dollar-Neutral');
Dollar-Neutral Portfolio with Maximum Sharpe Ratio
Weight Long Short
AA 0.5088 0.5088 0
AIG 3.0394 3.0394 0
AXP 0.92797 0.92797 0
BA -3.4952 0 3.4952
C 14.003 14.003 0
CAT 3.7261 3.7261 0
DD -18.063 0 18.063
DIS -4.8236 0 4.8236
GE -3.6178 0 3.6178
GM -3.7211 0 3.7211
HD 1.101 1.101 0
HON -1.4349 0 1.4349
HPQ 0.09909 0.09909 0
IBM -8.0585 0 8.0585
INTC 1.7693 1.7693 0
JNJ 1.3696 1.3696 0
JPM -2.5271 0 2.5271
KO -14.205 0 14.205
MCD 3.91 3.91 0
MMM 7.5995 7.5995 0
MO 4.0855 4.0855 0
MRK 3.747 3.747 0
MSFT 4.0769 4.0769 0
PFE -9.096 0 9.096
PG 1.6493 1.6493 0
SBC -5.2547 0 5.2547
UTX 5.7454 5.7454 0
VZ -2.438 0 2.438
WMT 0.84843 0.84843 0
XOM 18.529 18.529 0
Confirm Dollar-Neutral Portfolio
(Net, Long, Short)
0.0000 76.7350 76.7350
130/30 Fund Structure
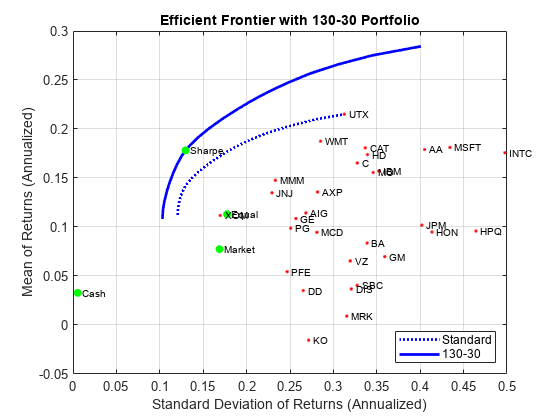
Finally, the turnover constraints are used to set up a 130-30 portfolio structure, which is a structure with a net long position but permits leverage with long and short positions up to a maximum amount of leverage. In the case of a 130-30 portfolio, the leverage is 30%.
To set up a 130-30 portfolio, start with the "standard" portfolio problem and set the maximum value for leverage in the variable Leverage. The bounds for individual asset weights range between -Leverage and 1 + Leverage. Since the net position must be long, the budget constraint is 1 and, once again, the initial portfolio is 0. Finally, the one-way turnover constraints provide the necessary long and short restrictions to prevent "double-counting" of long and short positions. The blotter shows the portfolio weights for the 130-30 portfolio that maximizes the Sharpe ratio. The long and short positions are obtained from the buy and sell trades relative to the initial portfolio.
Leverage = 0.3; q = setBounds(p, -Leverage, 1 + Leverage); q = setBudget(q, 1, 1); q = setOneWayTurnover(q, 1 + Leverage, Leverage); [qwgt,qbuy,qsell] = estimateFrontier(q,20); [qrsk,qret] = estimatePortMoments(q,qwgt); [qswgt,qslong,qsshort] = estimateMaxSharpeRatio(q); [qsrsk,qsret] = estimatePortMoments(q,qswgt); % Plot the efficient frontier for a 130-30 fund structure with tangency portfolio. clf; portfolioexamples_plot(sprintf('Efficient Frontier with %g-%g Portfolio', ... 100*(1 + Leverage),100*Leverage), ... {'line', prsk, pret, {'Standard'}, 'b:'}, ... {'line', qrsk, qret, {'130-30'}, 'b'}, ... {'scatter', qsrsk, qsret, {'Sharpe'}}, ... {'scatter', [mrsk, crsk, ersk], [mret, cret, eret], {'Market', 'Cash', 'Equal'}}, ... {'scatter', sqrt(diag(p.AssetCovar)), p.AssetMean, p.AssetList, '.r'});
% Set up a dataset object that contains the portfolio that maximizes the Sharpe ratio. Blotter = dataset({100*qswgt(abs(qswgt) > 1.0e-4), 'Weight'}, ... {100*qslong(abs(qswgt) > 1.0e-4), 'Long'}, ... {100*qsshort(abs(qswgt) > 1.0e-4), 'Short'}, ... 'obsnames', AssetList(abs(qswgt) > 1.0e-4)); displayPortfolio(sprintf('%g-%g Portfolio with Maximum Sharpe Ratio', 100*(1 + Leverage), 100*Leverage), Blotter, true, sprintf('%g-%g', 100*(1 + Leverage), 100*Leverage));
130-30 Portfolio with Maximum Sharpe Ratio
Weight Long Short
DD -9.5565 0 9.5565
HON -6.0244 0 6.0244
INTC 4.0335 4.0335 0
JNJ 7.1234 7.1234 0
JPM -0.44583 0 0.44583
KO -13.646 0 13.646
MMM 20.908 20.908 0
MO 14.433 14.433 0
MSFT 4.5592 4.5592 0
PG 17.243 17.243 0
SBC -0.32712 0 0.32712
UTX 5.3584 5.3584 0
WMT 21.018 21.018 0
XOM 35.323 35.323 0
Confirm 130-30 Portfolio
(Net, Long, Short)
100.0000 130.0000 30.0000
References
R. C. Grinold and R. N. Kahn. Active Portfolio Management. 2nd ed.,2000.
H. M. Markowitz. "Portfolio Selection." Journal of Finance. Vol. 1, No. 1, pp. 77-91, 1952.
J. Lintner. "The Valuation of Risk Assets and the Selection of Risky Investments in Stock Portfolios and Capital Budgets." Review of Economics and Statistics. Vol. 47, No. 1, pp. 13-37, 1965.
H. M. Markowitz. Portfolio Selection: Efficient Diversification of Investments. John Wiley & Sons, Inc., 1959.
W. F. Sharpe. "Mutual Fund Performance." Journal of Business. Vol. 39, No. 1, Part 2, pp. 119-138, 1966.
J. Tobin. "Liquidity Preference as Behavior Towards Risk." Review of Economic Studies. Vol. 25, No.1, pp. 65-86, 1958.
J. L. Treynor and F. Black. "How to Use Security Analysis to Improve Portfolio Selection." Journal of Business. Vol. 46, No. 1, pp. 68-86, 1973.
Local Functions
function displaySumOfTransactions(Turnover, qbuy, qsell) fprintf('Sum of Purchases by Portfolio along Efficient Frontier (Max. Turnover %g%%)\n', ... 100*Turnover); fprintf('%.4f ', 100*sum(qbuy)), sprintf('\n\n'); fprintf('\n') fprintf('Sum of Sales by Portfolio along Efficient Frontier (Max. Turnover %g%%)\n', ... 100*Turnover); fprintf('%.4f ', 100*sum(qsell)); end function displayPortfolio(Description, Blotter, LongShortFlag, portfolioType) fprintf('%s\n', Description); disp(Blotter); if (LongShortFlag) fprintf('Confirm %s Portfolio\n', portfolioType); fprintf(' (Net, Long, Short)\n'); fprintf('%.4f ' , [ sum(Blotter.Weight), sum(Blotter.Long), sum(Blotter.Short) ]); end end
See Also
Portfolio | setBounds | addGroups | setAssetMoments | estimateAssetMoments | estimateBounds | plotFrontier | estimateFrontierLimits | estimateFrontierByRisk | estimatePortRisk
Related Examples
- Creating the Portfolio Object
- Working with Portfolio Constraints Using Defaults
- Validate the Portfolio Problem for Portfolio Object
- Estimate Efficient Portfolios for Entire Efficient Frontier for Portfolio Object
- Estimate Efficient Frontiers for Portfolio Object
- Postprocessing Results to Set Up Tradable Portfolios
- Portfolio Optimization with Semicontinuous and Cardinality Constraints
- Black-Litterman Portfolio Optimization Using Financial Toolbox
- Portfolio Optimization Against a Benchmark
- Asset Allocation Case Study
- Portfolio Analysis with Turnover Constraints
- Leverage in Portfolio Optimization with a Risk-Free Asset
- Black-Litterman Portfolio Optimization Using Financial Toolbox
- Portfolio Optimization Using Factor Models
- Portfolio Optimization Using Social Performance Measure
- Diversify Portfolios Using Custom Objective
