Agency Option-Adjusted Spreads
Often bonds are issued with embedded options, which then makes standard price/yield or spread measures irrelevant. For example, a municipality concerned about the chance that interest rates may fall in the future might issue bonds with a provision that allows the bond to be repaid before the bond’s maturity. This is a call option on the bond and must be incorporated into the valuation of the bond. Option-adjusted spread (OAS), which adjusts a bond spread for the value of the option, is the standard measure for valuing bonds with embedded options. Financial Instruments Toolbox™ software supports computing option-adjusted spreads for bonds with single embedded options using the agency model.
The Securities Industry and Financial Markets Association (SIFMA) has a simplified
approach to compute OAS for agency issues (Government Sponsored Entities like Fannie Mae and
Freddie Mac) termed “Agency OAS”. In this approach, the bond has only one call
date (European call) and uses Black’s model (a variation on Black Scholes,
http://en.wikipedia.org/wiki/Black_model) to value the bond option. The price of
the bond is computed as follows:
PriceCallable =
PriceNonCallable –
PriceOption
where
PriceCallable is the price of the callable
bond.
PriceNonCallable is the price of the noncallable
bond, that is, price of the bond using bndspread.
PriceOption is the price of the option, that is,
price of the option using Black’s model.
The Agency OAS is the spread, when used in the previous formula, yields the market price. Financial Instruments Toolbox software supports these functions:
Agency OAS
Agency OAS Functions | Purpose |
|---|---|
Compute the OAS of the callable bond using the Agency OAS model. | |
Price the callable bond OAS using Agency using the OAS model. |
Computing the Agency OAS for Bonds
To compute the Agency OAS using agencyoas, you must provide the zero curve as the input
ZeroData. You can specify the zero curve in any intervals and with any
compounding method. You can do this using Financial Toolbox™ functions zbtprice and zbtyield. Or, you can use IRDataCurve to construct an IRDataCurve object, and then
use the getZeroRates to convert to dates and data
for use in the ZeroData input.
After creating the ZeroData input for agencyoas,
you can then:
Assign parameters for
CouponRate,Settle,Maturity,Vol,CallDate, andPrice.Compute the option-adjusted spread using
agencyoasto derive theOASoutput.If you have the Agency OAS for the callable bond, you can use the
OASvalue as an input toagencypriceto determine the price for a callable bond.
In the following example, the Agency OAS is computed using agencyoas for a range of bond prices and the spread of an identically priced
noncallable bond is calculated using bndspread.
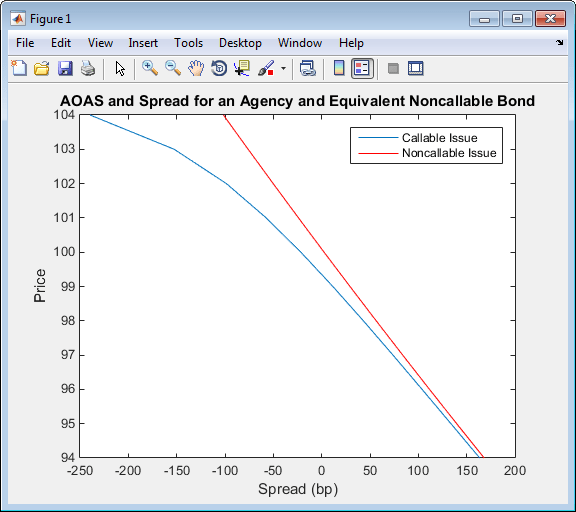
%% Data % Bond data -- note that there is only 1 call date Settle = datetime(2010,1,20); Maturity = datetime(2013,12,30); Coupon = .022; Vol = .5117; CallDate = datetime(2010,12,30); Period = 2; Basis = 1; Face = 100; % Zero Curve data ZeroTime = [.25 .5 1 2 3 4 5 7 10 20 30]'; ZeroDates = daysadd(Settle,360*ZeroTime,1); ZeroRates = [.0008 .0017 .0045 .0102 .0169 .0224 .0274 .0347 .0414 .0530 .0740]'; ZeroData = [ZeroDates ZeroRates]; CurveCompounding = 2; CurveBasis = 1; Price = 94:104; OAS = agencyoas(ZeroData, Price', Coupon, Settle,Maturity, Vol, CallDate,'Basis',Basis) Spread = bndspread(ZeroData, Price', Coupon, Settle, Maturity) plot(OAS,Price) hold on plot(Spread,Price,'r') xlabel('Spread (bp)') ylabel('Price') title('AOAS and Spread for an Agency and Equivalent Noncallable Bond') legend({'Callable Issue','Noncallable Issue'})
OAS =
163.4942
133.7306
103.8735
73.7505
43.1094
11.5608
-21.5412
-57.3869
-98.5675
-152.5226
-239.6462
Spread =
168.1412
139.7047
111.6123
83.8561
56.4286
29.3227
2.5314
-23.9523
-50.1348
-76.0226
-101.6218The following plot demonstrates as the price increases, the value of the embedded option in the Agency issue increases, and the value of the issue itself does not increase as much as it would for a noncallable bond, illustrating the negative convexity of this issue: