bktree
Build Black-Karasinski interest-rate tree
Description
Examples
Input Arguments
Output Arguments
References
[1] Hull, J., and A. White. "Using Hull-White Interest Rate Trees." Journal of Derivatives. 1996.
[2] Hull, J., and A. White. "The General Hull-White Model and Super Calibration." August 2000.
Version History
Introduced before R2006a
See Also
bkprice | bkvolspec | bktimespec | intenvset | bksens
Topics
- Pricing Using Interest-Rate Tree Models
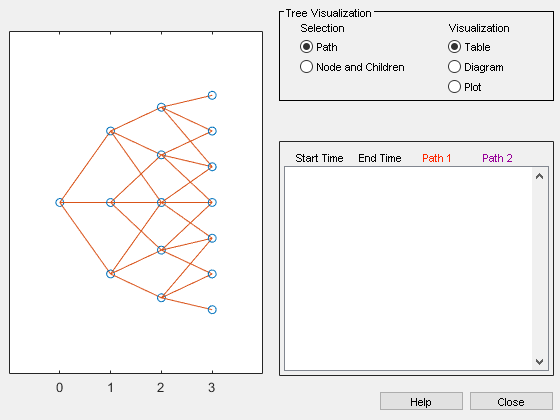
- Use treeviewer to Examine HWTree and PriceTree When Pricing European Callable Bond
- Calibrating Hull-White Model Using Market Data
- Pricing Options Structure
- Understanding Interest-Rate Tree Models
- Supported Interest-Rate Instrument Functions
- Mapping Financial Instruments Toolbox Functions for Interest-Rate Instrument Objects