Hedging Functions
Introduction
Hedging is an investment to reduce the risk of adverse price movements in an asset.
Financial Instruments Toolbox™ offers two functions for assessing the fundamental hedging tradeoff, hedgeopt and hedgeslf.
The first function, hedgeopt, addresses the most general
hedging problem. It allocates an optimal hedge to satisfy either of two goals:
Minimize the cost of hedging a portfolio given a set of target sensitivities.
Minimize portfolio sensitivities for a given set of maximum target costs.
hedgeopt allows investors
to modify portfolio allocations among instruments according to either
of the goals. The problem is cast as a constrained linear least-squares
problem. For additional information about hedgeopt,
see Hedging with hedgeopt.
The second function, hedgeslf, attempts to allocate a
self-financing hedge among a portfolio of instruments. In particular, hedgeslf attempts to maintain a constant portfolio value consistent with
reduced portfolio sensitivities (that is, the rebalanced portfolio is hedged against market
moves and is closest to being self-financing). If hedgeslf cannot find a self-financing hedge, it rebalances the portfolio to
minimize overall portfolio sensitivities. For additional information on hedgeslf, see Self-Financing Hedges with hedgeslf.
The examples in this section consider the delta,
gamma, and vega sensitivity measures. In this
toolbox, when you work with interest-rate derivatives, delta is the
price sensitivity measure of shifts in the forward yield curve, gamma is the delta
sensitivity measure of shifts in the forward yield curve, and vega is the price sensitivity
measure of shifts in the volatility process. See bdtsens or hjmsens for details on the computation of
sensitivities for interest-rate derivatives.
For equity exotic options, the underlying
instrument is the stock price instead of the forward yield curve.
So, delta now represents the price sensitivity measure of shifts in
the stock price, gamma is the delta sensitivity measure of shifts
in the stock price, and vega is the price sensitivity measure of shifts
in the volatility of the stock. See crrsens, eqpsens, ittsens,
or sttsens for details on the
computation of sensitivities for equity derivatives.
For examples showing the computation of sensitivities for interest-rate based derivatives, see Computing Instrument Sensitivities. Likewise, for examples showing the computation of sensitivities for equity exotic options, see Computing Equity Instrument Sensitivities.
Note
The delta, gamma, and vega sensitivities that the toolbox calculates are dollar sensitivities.
Hedging with hedgeopt
Note
The numerical results in this section are displayed in the MATLAB® bank format. Although the calculations are performed in floating-point double precision, only two decimal places are displayed.
To illustrate the hedging facility, consider the portfolio HJMInstSet obtained
from the example file deriv.mat. The portfolio
consists of eight instruments: two bonds, one bond option, one fixed-rate
note, one floating-rate note, one cap, one floor, and one swap.
Both hedging functions require some common inputs, including the current portfolio holdings (allocations), and a matrix of instrument sensitivities. To create these inputs, load the example portfolio into memory
load deriv.mat;
compute price and sensitivities
[Delta, Gamma, Vega, Price] = hjmsens(HJMTree, HJMInstSet);
Warning: Not all cash flows are aligned with the tree. Result will be approximated.
and extract the current portfolio holdings.
Holdings = instget(HJMInstSet, 'FieldName', 'Quantity');
For convenience place the delta, gamma, and vega sensitivity measures into a matrix of sensitivities.
Sensitivities = [Delta Gamma Vega];
Each row of the Sensitivities matrix is associated
with a different instrument in the portfolio, and each column with
a different sensitivity measure.
To summarize the portfolio information
disp([Price Holdings Sensitivities])
98.72 100.00 -272.65 1029.90 0.00 97.53 50.00 -347.43 1622.69 -0.04 0.05 -50.00 -8.08 643.40 34.07 98.72 80.00 -272.65 1029.90 0.00 100.55 8.00 -1.04 3.31 0 6.28 30.00 294.97 6852.56 93.69 0.05 40.00 -47.16 8459.99 93.69 3.69 10.00 -282.05 1059.68 0.00
The first column above is the dollar unit price of each instrument, the second is the holdings of each instrument (the quantity held or the number of contracts), and the third, fourth, and fifth columns are the dollar delta, gamma, and vega sensitivities, respectively.
The current portfolio sensitivities are a weighted average of the instruments in the portfolio.
TargetSens = Holdings' * Sensitivities
TargetSens =
-61910.22 788946.21 4852.91Maintaining Existing Allocations
To illustrate using hedgeopt,
suppose that you want to maintain your existing portfolio. The first
form of hedgeopt minimizes the cost of hedging
a portfolio given a set of target sensitivities. If you want to maintain
your existing portfolio composition and exposure, you should be able
to do so without spending any money. To verify this, set the target
sensitivities to the current sensitivities.
FixedInd = [1 2 3 4 5 6 7 8]; [Sens, Cost, Quantity] = hedgeopt(Sensitivities, Price,Holdings, FixedInd, [], [], TargetSens)
Holdings =
100.00
50.00
-50.00
80.00
8.00
30.00
40.00
10.00
Sens =
-61910.22 788946.21 4852.91
Cost =
0
Quantity =
Columns 1 through 6
100.00 50.00 -50.00 80.00 8.00 30.00
Columns 7 through 8
40.00 10.00Portfolio composition and sensitivities are unchanged, and the cost associated with doing nothing is zero. The cost is defined as the change in portfolio value. This number cannot be less than zero because the rebalancing cost is defined as a nonnegative number.
If Value0 and Value1 represent
the portfolio value before and after rebalancing, respectively, the
zero cost can also be verified by comparing the portfolio values.
Value0 = Holdings' * Price
Value0 =
23674.62
Value1 = Quantity * Price
Value1 =
23674.62Partially Hedged Portfolio
Building on the example in Maintaining Existing Allocations, suppose you want to know
the cost to achieve an overall portfolio dollar sensitivity of [-23000
-3300 3000], while allowing trading only in instruments
2, 3, and 6 (holding the positions of instruments 1, 4, 5, 7, and
8 fixed). To find the cost, first set the target portfolio dollar
sensitivity.
TargetSens = [-23000 -3300 3000];
Then, specify the instruments to be fixed.
FixedInd = [1 4 5 7 8];
Finally, call hedgeopt
[Sens, Cost, Quantity] = hedgeopt(Sensitivities, Price,... Holdings, FixedInd, [], [], TargetSens);
and again examine the results.
Sens =
-23000.00 -3300.00 3000.00
Cost =
19174.02
Quantity' =
100.00
-141.03
137.26
80.00
8.00
-57.96
40.00
10.00
Recompute Value1, the portfolio value after
rebalancing.
Value1 = Quantity * Price
Value1 =
4500.60
As expected, the cost, $19174.02, is the difference between Value0 and Value1,
$23674.62 — $4500.60. Only the positions in instruments 2,
3, and 6 have been changed.
Fully Hedged Portfolio
The example in Partially Hedged Portfolio illustrates a partial hedge, but
perhaps the most interesting case involves the cost associated with
a fully hedged portfolio (simultaneous delta, gamma, and vega neutrality).
In this case, set the target sensitivity to a row vector of 0s and
call hedgeopt again. The following
example uses data from Hedging with hedgeopt.
TargetSens = [0 0 0]; [Sens, Cost, Quantity] = hedgeopt(Sensitivities, Price, ... Holdings, FixedInd, [], [], TargetSens);
Examining the outputs reveals that you have obtained a fully hedged portfolio
Sens =
-0.00 -0.00 -0.00
but at an expense of over $20,000.
Cost =
23055.90
The positions required to achieve a fully hedged portfolio
Quantity' =
100.00
-182.36
-19.55
80.00
8.00
-32.97
40.00
10.00
result in the new portfolio value
Value1 = Quantity * Price
Value1 =
618.72Minimizing Portfolio Sensitivities
The examples in Fully Hedged Portfolio illustrate how to use hedgeopt to determine the minimum cost
of hedging a portfolio given a set of target sensitivities. In these
examples, portfolio target sensitivities are treated as equality constraints
during the optimization process. You tell hedgeopt what
sensitivities you want, and it tells you what it will cost to get
those sensitivities.
A related problem involves minimizing portfolio sensitivities
for a given set of maximum target costs. For this goal, the target
costs are treated as inequality constraints during the optimization
process. You tell hedgeopt the
most you are willing spend to insulate your portfolio, and it tells
you the smallest portfolio sensitivities you can get for your money.
To illustrate this use of hedgeopt,
compute the portfolio dollar sensitivities along the entire cost frontier.
From the previous examples, you know that spending nothing replicates
the existing portfolio, while spending $23,055.90 completely hedges
the portfolio.
Assume, for example, you are willing to spend as much as $50,000, and want to see what portfolio sensitivities will result along the cost frontier. Assume that the same instruments are held fixed, and that the cost frontier is evaluated from $0 to $50,000 at increments of $1000.
MaxCost = [0:1000:50000];
Now, call hedgeopt.
[Sens, Cost, Quantity] = hedgeopt(Sensitivities, Price, ... Holdings, FixedInd, [], MaxCost);
With this data, you can plot the required hedging cost versus the funds available (the amount you are willing to spend)
plot(MaxCost/1000, Cost/1000, 'red'), grid xlabel('Funds Available for Rebalancing ($1000''s)') ylabel('Actual Rebalancing Cost ($1000''s)') title ('Rebalancing Cost Profile')
Rebalancing Cost Profile
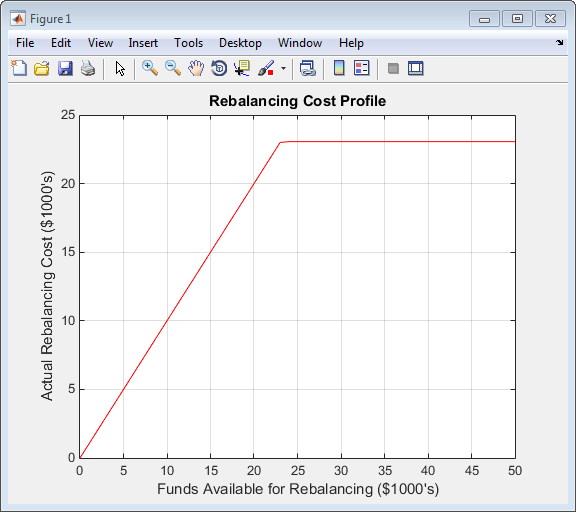
and the portfolio dollar sensitivities versus the funds available.
figure plot(MaxCost/1000, Sens(:,1), '-red') hold('on') plot(MaxCost/1000, Sens(:,2), '-.black') plot(MaxCost/1000, Sens(:,3), '--blue') grid xlabel('Funds Available for Rebalancing ($1000''s)') ylabel('Delta, Gamma, and Vega Portfolio Dollar Sensitivities') title ('Portfolio Sensitivities Profile') legend('Delta', 'Gamma', 'Vega', 0)
Funds Available for Rebalancing
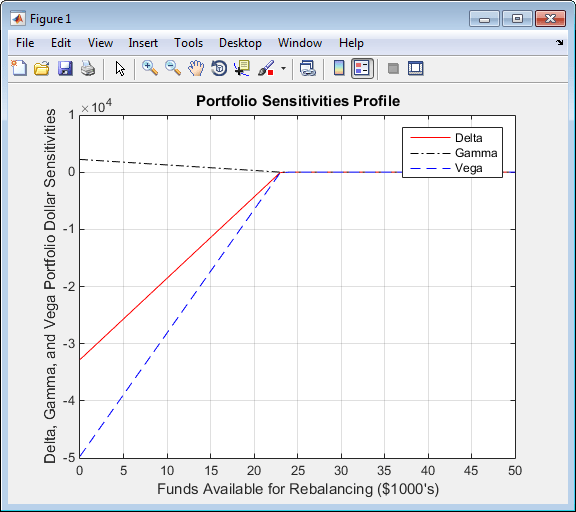
Self-Financing Hedges with hedgeslf
The figures Rebalancing Cost Profile and Funds Available for Rebalancing indicate that there is no
benefit because the funds available for hedging exceed $23,055.90,
the point of maximum expense required to obtain simultaneous delta,
gamma, and vega neutrality. You can also find this point of delta,
gamma, and vega neutrality using hedgeslf.
[Sens, Value1, Quantity] = hedgeslf(Sensitivities, Price,... Holdings, FixedInd);
Sens =
-0.00
-0.00
-0.00
Value1 =
618.72
Quantity =
100.00
-182.36
-19.55
80.00
8.00
-32.97
40.00
10.00
Similar to hedgeopt, hedgeslf returns the portfolio dollar
sensitivities and instrument quantities (the rebalanced holdings).
However, in contrast, the second output parameter of hedgeslf is the value of the rebalanced
portfolio, from which you can calculate the rebalancing cost by subtraction.
Value0 - Value1
ans =
23055.90
In this example, the portfolio is clearly not self-financing,
so hedgeslf finds the best
possible solution required to obtain zero sensitivities.
There is, in fact, a third calling syntax available for hedgeopt directly related to the results
shown above for hedgeslf. Suppose,
instead of directly specifying the funds available for rebalancing
(the most money you are willing to spend), you want to simply specify
the number of points along the cost frontier. This call to hedgeopt samples the cost frontier at
10 equally spaced points between the point of minimum cost (and potentially
maximum exposure) and the point of minimum exposure (and maximum cost).
[Sens, Cost, Quantity] = hedgeopt(Sensitivities, Price,... Holdings, FixedInd, 10)
Sens =
-32784.46 2231.83 -49694.33
-29141.74 1983.85 -44172.74
-25499.02 1735.87 -38651.14
-21856.30 1487.89 -33129.55
-18213.59 1239.91 -27607.96
-14570.87 991.93 -22086.37
-10928.15 743.94 -16564.78
-7285.43 495.96 -11043.18
-3642.72 247.98 -5521.59
0.00 -0.00 0.00
Cost =
0.00
2561.77
5123.53
7685.30
10247.07
12808.83
15370.60
17932.37
20494.14
23055.90
Now plot this data.
figure plot(Cost/1000, Sens(:,1), '-red') hold('on') plot(Cost/1000, Sens(:,2), '-.black') plot(Cost/1000, Sens(:,3), '--blue') grid xlabel('Rebalancing Cost ($1000''s)') ylabel('Delta, Gamma, and Vega Portfolio Dollar Sensitivities') title ('Portfolio Sensitivities Profile') legend('Delta', 'Gamma', 'Vega', 0)
Rebalancing Cost
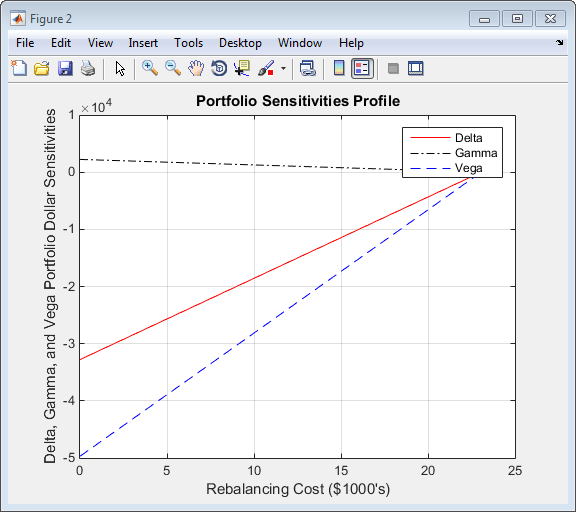
In this calling form, hedgeopt calls hedgeslf internally to determine the
maximum cost needed to minimize the portfolio sensitivities ($23,055.90),
and evenly samples the cost frontier between $0 and $23,055.90.
Both hedgeopt and hedgeslf cast the optimization problem
as a constrained linear least squares problem. Depending on the instruments
and constraints, neither function is guaranteed to converge to a solution.
In some cases, the problem space may be unbounded, and additional
instrument equality constraints, or user-specified constraints, may
be necessary for convergence. See Hedging with Constrained Portfolios for
additional information.
See Also
Related Examples
- Portfolio Creation Using Functions
- Adding Instruments to an Existing Portfolio Using Functions
- Instrument Constructors
- Creating Instruments or Properties
- Searching or Subsetting a Portfolio
- Pricing a Portfolio Using the Black-Derman-Toy Model
- Pricing and Hedging a Portfolio Using the Black-Karasinski Model
- Specifying Constraints with ConSet
- Portfolio Rebalancing
- Hedging with Constrained Portfolios
