Precision
Computer words consist of a finite number of bits. This means that the binary encoding of variables is only an approximation of an arbitrarily precise real-world value. Therefore, the limitations of the binary representation automatically introduce limitations on the precision of the value.
Topics
- Range and Precision
Range and precision of fixed-point data types.
- Maximize Precision
To maximize precision, make the slope as small as possible while keeping the range adequately large.
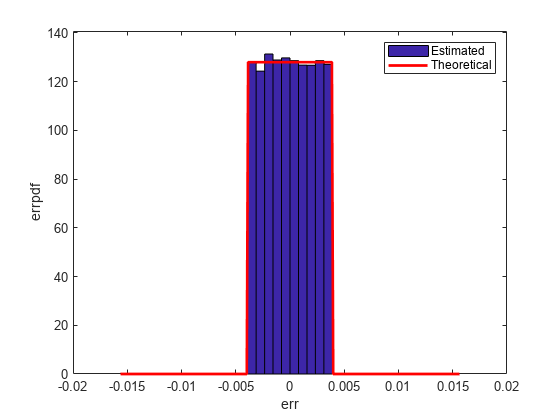
- Rounding
Rounding involves going from high precision to lower precision and produces quantization errors and computational noise.
- Rounding Modes for Fixed-Point Simulink Blocks
Fixed-point Simulink® blocks support seven different rounding modes.
- Net Slope and Net Bias Precision
Net slope and bias precision, detecting precision loss, underflow, and overflow.
- Detect Fixed-Point Constant Precision Loss
This example shows how to detect fixed-point constant precision loss.
- Use Scaled Doubles to Avoid Precision Loss
How to avoid precision loss by overriding the data types in your model with scaled doubles.