cordicatan2
CORDIC-based four quadrant inverse tangent
Description
Examples
Compute CORDIC Arctangent
Define floating-point Cartesian coordinates.
y = 0.5; x = -0.5;
Use cordicatan2 to compute floating-point CORDIC arctangent. Compare the result to the arctangent computed using atan2.
theta_cdat2_float = cordicatan2(y,x)
theta_cdat2_float = 2.3562
theta_atan2_float = atan2(y,x)
theta_atan2_float = 2.3562
Define fixed-point Cartesian coordinates.
y = fi(0.5,1,16,15); x = fi(-0.5,1,16,15);
Use cordicatan2 to compute fixed-point CORDIC arctangent. Compare the result to the arctangent computed using atan2.
theta_cdat2_fixpt = cordicatan2(y,x)
theta_cdat2_fixpt =
2.3562
DataTypeMode: Fixed-point: binary point scaling
Signedness: Signed
WordLength: 16
FractionLength: 13
theta_atan2_fixpt = atan2(y,x)
theta_atan2_fixpt =
2.3562
DataTypeMode: Fixed-point: binary point scaling
Signedness: Signed
WordLength: 16
FractionLength: 13
Input Arguments
y — Cartesian y-coordinate
scalar | vector | matrix | multidimensional array
Cartesian y-coordinate, specified as a scalar, vector, matrix, or multidimensional array.
y and x must be the same size. If they are
not the same size, at least one value must be a scalar value. y and
x must have the same data type.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | fi
Complex Number Support: Yes
x — Cartesian x-coordinate
scalar | vector | matrix | multidimensional array
Cartesian x-coordinate, specified as a scalar, vector, matrix, or multidimensional array.
y and x must be the same size. If they are
not the same size, at least one value must be a scalar value. y and
x must have the same data type.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | fi
Complex Number Support: Yes
niters — Number of iterations of CORDIC algorithm
positive integer-valued scalar
Number of iterations of CORDIC algorithm, specified as a positive, integer-valued scalar.
Increasing the number of iterations can produce more accurate results, but also increases the expense of the computation and adds latency.
If you do not specify niters, or if you specify a value that is
too large, the algorithm uses a maximum value. For fixed-point operation, the maximum
number of iterations is one less than the word length of y or
x. For floating-point operation, the maximum value is 52 for
double or 23 for single.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | fi
Output Arguments
theta — Arctangent value
scalar | vector | matrix | multidimensional array
Arctangent value in the range [-pi, pi] radians, returned as a scalar, vector, matrix, or multidimensional array.
If y and x are floating-point numbers,
then theta has the same data type as y and
x. Otherwise, theta is a fixed-point data
type with the same word length as y and x and
with a best-precision fraction length for the [-pi, pi] range.
Algorithms
CORDIC
CORDIC is an acronym for COordinate Rotation DIgital Computer. The Givens rotation-based CORDIC algorithm is one of the most hardware-efficient algorithms available because it requires only iterative shift-add operations (see References). The CORDIC algorithm eliminates the need for explicit multipliers. Using CORDIC, you can calculate various functions such as sine, cosine, arc sine, arc cosine, arc tangent, and vector magnitude. You can also use this algorithm for divide, square root, hyperbolic, and logarithmic functions.
Increasing the number of CORDIC iterations can produce more accurate results, but doing so increases the expense of the computation and adds latency.
Signal Flow Diagram
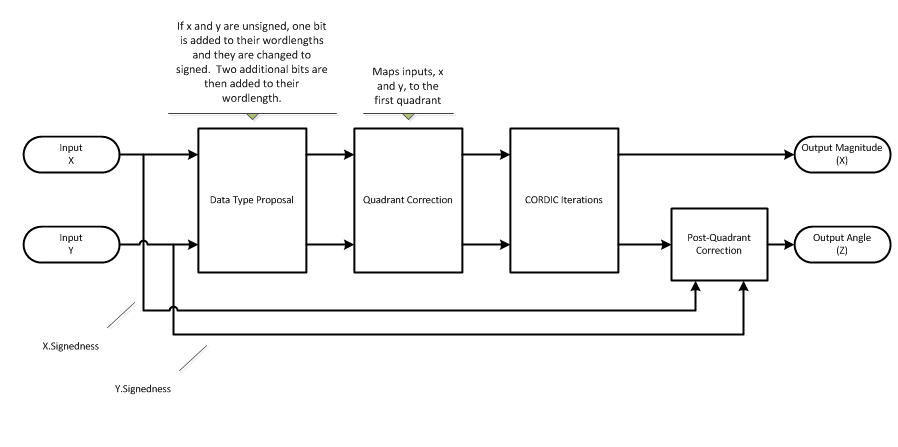
CORDIC Vectoring Kernel
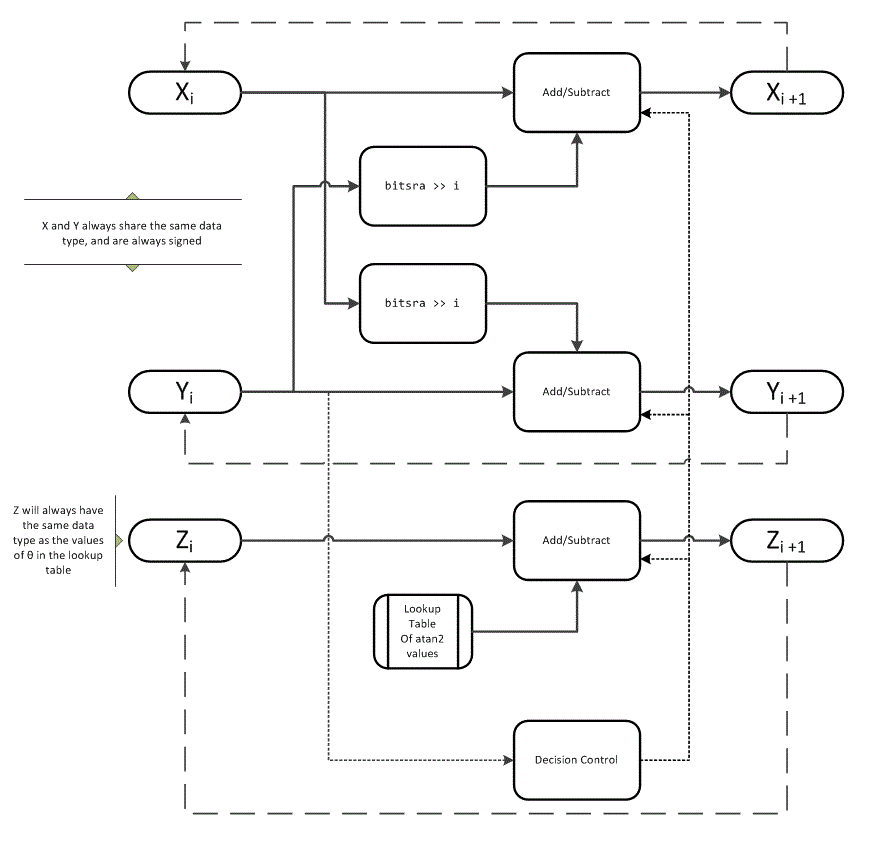
The accuracy of the CORDIC kernel depends on the choice of initial values for X, Y, and Z. This algorithm uses the following initial values:
X0 is initialized to the X input value
Y0 is initialized to the Y input value
Z0 is initialized
0
fimath Propagation Rules
CORDIC functions discard any local fimath attached to the
input.
The CORDIC functions use their own internal fimath when performing calculations:
OverflowAction—WrapRoundingMethod—Floor
The output has no attached fimath.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
Usage notes and limitations:
Variable-size signals are not supported.
The number of iterations the CORDIC algorithm performs,
niters, must be a constant.
HDL Code Generation
Generate VHDL, Verilog and SystemVerilog code for FPGA and ASIC designs using HDL Coder™.
The cordicatan2 function also supports MATLAB® to High-Level Synthesis (HLS) code generation.
Version History
Introduced in R2011b
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)