Minimize Function with Many Local Minima
This example shows how to find a local minimum of a function using simulated annealing. The example presents two approaches for minimizing: working at the command line and using the Optimize Live Editor task.
De Jong's fifth function is a two-dimensional function with many (25) local minima. The function is available when you run this example. In the following plot, it is unclear which of the local minima is the global minimum.
dejong5fcn

Many standard optimization algorithms become stuck in local minima. Because the simulated annealing algorithm performs a wide random search, the chance of being trapped in a local minimum is decreased.
Note:Because simulated annealing uses random number generators, each time you run this algorithm you can get different results. See Reproduce Your Results for more information.
Minimize at the Command Line
To run the simulated annealing algorithm without constraints, call simulannealbnd at the command line using the objective function in dejong5fcn.m, referenced by the anonymous function @dejong5fcn in the following code.
rng(10,'twister') % for reproducibility fun = @dejong5fcn; [x,fval] = simulannealbnd(fun,[0 0])
simulannealbnd stopped because the change in best function value is less than options.FunctionTolerance.
x = 1×2
-16.1292 -15.8214
fval = 6.9034
In the results:
x is the final point returned by the algorithm.
fval is the objective function value at the final point.
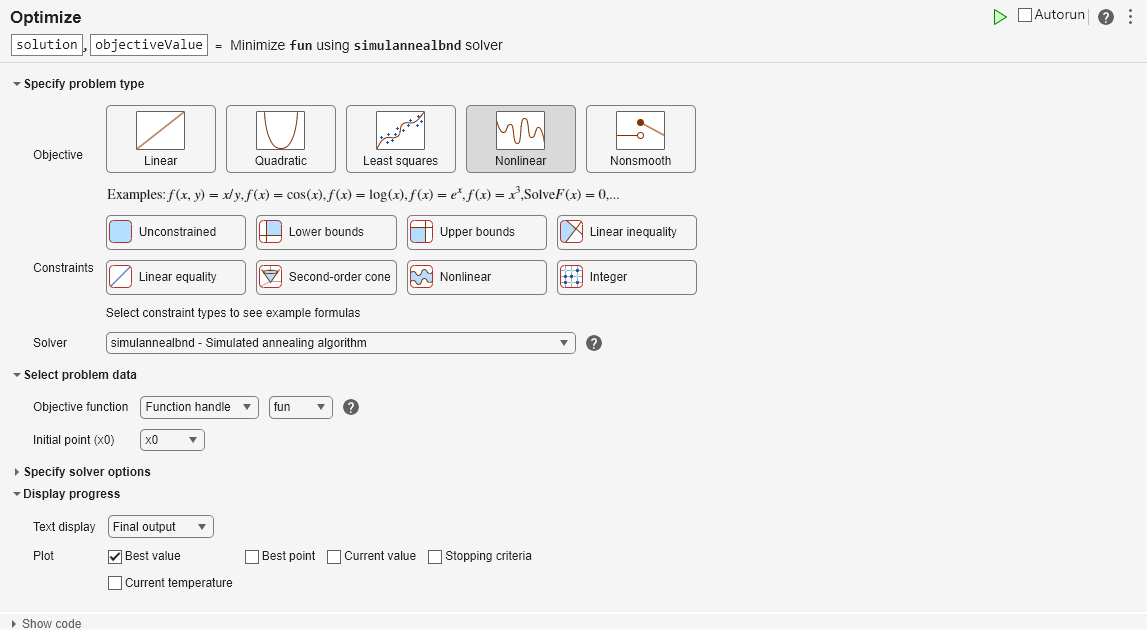
Minimize Using the Optimize Live Editor Task
You can also run the minimization using the Optimize Live Editor task, which provides a visual approach.
Create a new live script by clicking the New Live Script button in the File section on the Home tab.

Insert an
OptimizeLive Editor task. Click the Insert tab and then, in the Code section, select Task > Optimize.


Click the Solver-based task.

For use in entering problem data, insert a new section by clicking the Section Break button on the Insert tab. New sections appear above and below the task.
In the new section above the task, enter the following code to define the initial point and the objective function.
x0 = [0 0]; fun = @dejong5fcn; rng default % For reproducibility
To place these variables into the workspace, run the section by pressing Ctrl+Enter.
In the Specify problem type section of the task, click the Objective > Nonlinear button.
Select Solver > simulannealbnd - Simulated annealing algorithm.
In the Select problem data section of the task, select Objective function > Function handle and then choose
fun.Select Initial point (x0) > x0.

In the Display progress section of the task, select the Best value plot.
To run the solver, click the options button ⁝ at the top right of the task window, and select Run Section. The plot appears in a separate figure window and in the task output area. Note that your plot might be different from the one shown, because
simulannealbndis a stochastic algorithm.

To see the solution and best objective function value, look at the top of the task.
![]()
The
OptimizeLive Editor task returns variables namedsolutionandobjectiveValueto the workspace.To view the values these variables, enter the following code in the section below the task.
disp(solution) disp(objectiveValue)
Run the section by pressing Ctrl+Enter.
The end of this example has the Optimize task in its final state.

simulannealbnd stopped because the change in best function value is less than options.FunctionTolerance.
Both the Optimize Live Editor task and the command line allow you to formulate and solve problems, and they give identical results. The command line is more streamlined, but provides less help for choosing a solver, setting up the problem, and choosing options such as plot functions. You can also start a problem using Optimize, and then generate code for command line use, as in Constrained Nonlinear Problem Using Optimize Live Editor Task or Solver.
