Mixed Integer ga Optimization
Solving Mixed Integer Optimization Problems
ga can solve problems when certain variables are
integer-valued. Give intcon, a vector of the x
components that are integers:
[x,fval,exitflag] = ga(fitnessfcn,nvars,A,b,[],[],...
lb,ub,nonlcon,intcon,options)intcon is a vector of positive integers that contains the
x components that are integer-valued. For example, if you
want to restrict x(2) and x(10) to be
integers, set intcon to [2,10].
The surrogateopt solver also accepts integer constraints.
Note
Restrictions exist on the types of problems that ga can
solve with integer variables. In particular, ga does not
accept nonlinear equality constraints when there are integer variables. For
details, see Characteristics of the Integer ga Solver.
Tip
ga solves integer problems best when you provide lower
and upper bounds for every x component.
Mixed Integer Optimization of Rastrigin's Function
This example shows how to find the minimum of Rastrigin's function restricted so the first component of x is an integer. The components of x are further restricted to be in the region .
Set up the bounds for your problem
lb = [5*pi,-20*pi]; ub = [20*pi,-4*pi];
Set a plot function so you can view the progress of ga
opts = optimoptions('ga','PlotFcn',@gaplotbestf);
Call the ga solver where x(1) has integer values
rng(1,'twister') % for reproducibility intcon = 1; [x,fval,exitflag] = ga(@rastriginsfcn,2,[],[],[],[],... lb,ub,[],intcon,opts)
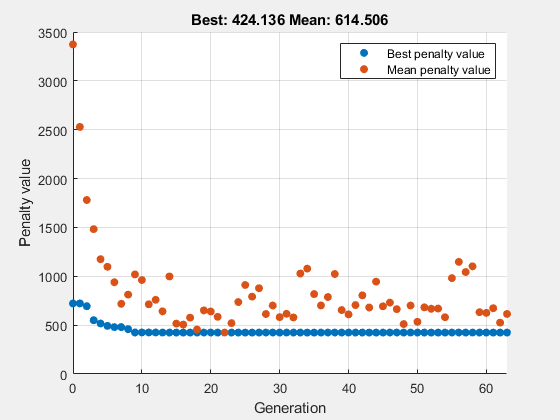
ga stopped because the average change in the penalty function value is less than options.FunctionTolerance and the constraint violation is less than options.ConstraintTolerance.
x = 1×2
16.0000 -12.9325
fval = 424.1355
exitflag = 1
ga converges quickly to the solution.
Characteristics of the Integer ga Solver
There are some restrictions on the types of problems that ga
can solve when you include integer constraints:
No nonlinear equality constraints. Any nonlinear constraint function must return
[]for the nonlinear equality constraint. For a possible workaround, see Integer Programming with a Nonlinear Equality Constraint.Only
doubleVectorpopulation type.No hybrid function.
gaoverrides any setting of theHybridFcnoption.gaignores theParetoFraction,DistanceMeasureFcn,InitialPenalty, andPenaltyFactoroptions.
The listed restrictions are mainly natural, not arbitrary. For example, no hybrid
functions support integer constraints. So ga does not use
hybrid functions when there are integer constraints.
Integer Programming with a Nonlinear Equality Constraint
This example attempts to locate the minimum of the Ackley function (included when you run this example) in five dimensions with these constraints:
x(1),x(3), andx(5)are integers.norm(x) = 4.
The ga solver does not support nonlinear equality constraints, only nonlinear inequality constraints. This example shows a workaround that applies for some problems, but is not guaranteed to work.
The Ackley function is difficult to minimize. Adding integer and equality constraints increases the difficulty.
To include the nonlinear equality constraint, give a small tolerance tol that allows the norm of x to be within tol of 4. Without a tolerance, the nonlinear equality constraint is never satisfied, and the solver does not reach a feasible solution.
Write the expression norm(x) = 4 as two “less than zero” inequalities.
.
Allow a small tolerance in the inequalities.
.
Write a nonlinear inequality constraint function eqCon that implements these inequalities.
type eqConfunction [c, ceq] = eqCon(x) ceq = []; rad = 4; tol = 1e-3; confcnval = norm(x) - rad; c = [confcnval - tol;-confcnval - tol];
Set these options:
MaxStallGenerations= 50 — Allow the solver to try for a while.FunctionTolerance= 1e-10 — Specify a stricter stopping criterion than usual.MaxGenerations= 500 — Allow more generations than default.PlotFcn=@gaplotbestfun— Observe the optimization.
opts = optimoptions('ga','MaxStallGenerations',50,'FunctionTolerance',1e-10,... 'MaxGenerations',500,'PlotFcn',@gaplotbestfun);
Set lower and upper bounds to help the solver.
nVar = 5; lb = -5*ones(1,nVar); ub = 5*ones(1,nVar);
Solve the problem.
rng(0,'twister') % for reproducibility [x,fval,exitflag] = ga(@ackleyfcn,nVar,[],[],[],[], ... lb,ub,@eqCon,[1 3 5],opts);
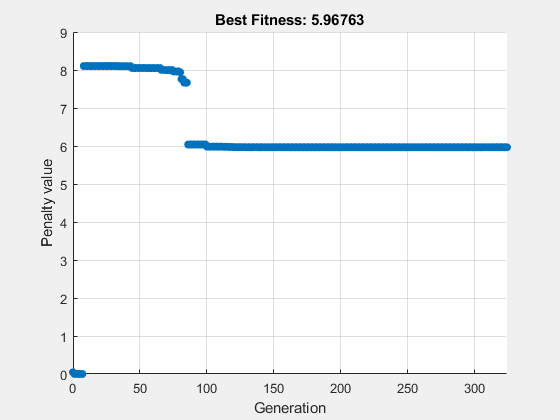
ga stopped because the average change in the penalty function value is less than options.FunctionTolerance and the constraint violation is less than options.ConstraintTolerance.
Examine the solution.
x,fval,exitflag,norm(x)
x = 1×5
0 0.9706 1.0000 3.6158 -1.0000
fval = 5.9676
exitflag = 1
ans = 4.0020
The odd x components are integers, as specified. The norm of x is 4, to within the given relative tolerance of 1e-3.
Despite the positive exit flag, the solution is not the global optimum. Run the problem again with a larger population and examine the solution.
opts = optimoptions(opts,'Display','off','PopulationSize',400); [x2,fval2,exitflag2] = ga(@ackleyfcn,nVar,[],[],[],[], ... lb,ub,@eqCon,[1 3 5],opts);
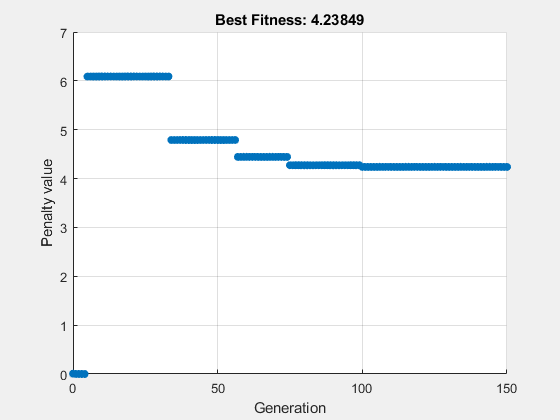
Examine the second solution.
x2,fval2,exitflag2,norm(x2)
x2 = 1×5
-1.0000 2.0082 -1.0000 -2.9954 1.0000
fval2 = 4.2385
exitflag2 = 1
ans = 4.0006
The second run gives a better solution (lower fitness function value). Again, the odd x components are integers, and the norm of x2 is 4, to within the given relative tolerance of 1e-3.
Be aware that this procedure can fail; ga has difficulty with simultaneous integer and nonlinear equality constraints.
Effective Integer ga
To use ga most effectively on integer problems, follow these
guidelines.
Bound each component as tightly as you can. This practice gives
gathe smallest search space, enablinggato search most effectively.If you cannot bound a component, then specify an appropriate initial range. By default,
gacreates an initial population with range[-1e4,1e4]for each component. A smaller or larger initial range can give better results when the default value is inappropriate. To change the initial range, use theInitialPopulationRangeoption.If you have more than 10 variables, set a population size that is larger than default by using the
PopulationSizeoption. The default value is 200 for six or more variables. For a large population size:gacan take a long time to converge. If you reach the maximum number of generations (exit flag0), increase the value of theMaxGenerationsoption.Decrease the mutation rate. To do so, increase the value of the
CrossoverFractionoption from its default of0.8to0.9or higher.Increase the value of the
EliteCountoption from its default of0.05*PopulationSizeto0.1*PopulationSizeor higher.
For information on options, see the ga
options
input argument.
Integer ga Algorithm
Integer programming with ga involves several modifications of
the basic algorithm (see How the Genetic Algorithm Works). For integer
programming:
By default, special creation, crossover, and mutation functions enforce variables to be integers. For details, see Deep et al. [2].
If you use nondefault creation, crossover, or mutation functions,
gaenforces linear feasibility and feasibility with respect to integer constraints at each iteration.The genetic algorithm attempts to minimize a penalty function, not the fitness function. The penalty function includes a term for infeasibility. This penalty function is combined with binary tournament selection by default to select individuals for subsequent generations. The penalty function value of a member of a population is:
If the member is feasible, the penalty function is the fitness function.
If the member is infeasible, the penalty function is the maximum fitness function among feasible members of the population, plus a sum of the constraint violations of the (infeasible) point.
For details of the penalty function, see Deb [1].
References
[1] Deb, Kalyanmoy. An efficient constraint handling method for genetic algorithms. Computer Methods in Applied Mechanics and Engineering, 186(2–4), pp. 311–338, 2000.
[2] Deep, Kusum, Krishna Pratap Singh, M.L. Kansal, and C. Mohan. A real coded genetic algorithm for solving integer and mixed integer optimization problems. Applied Mathematics and Computation, 212(2), pp. 505–518, 2009.
