compare
Compare identified model output with measured output
Syntax
Description
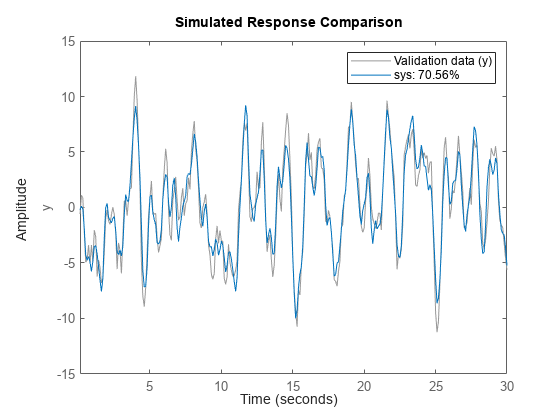
Plot Simulated and Measured Outputs
compare(
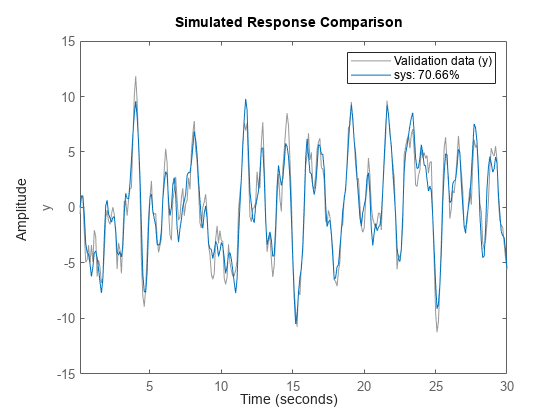
simulates the response of a single dynamic system model data,sys)sys or an
array of dynamic system models, and superimposes the response for each model over the
plotted input/output measurement data contained in data.
data can be a timetable, a comma-separated input/output matrix
pair, or a data object such as an iddata object or an idfrd object.
The plot also displays the normalized root mean square (NRMSE) measure of the goodness of the fit between the simulated response and the output measurement data.
Use this function when you want to validate a single model or when you want to evaluate a set of candidate models identified from the same measurement data.
For timetables and data objects, compare matches the input/output
channels based on the channel names in sys and ignores nonmatching
channels.
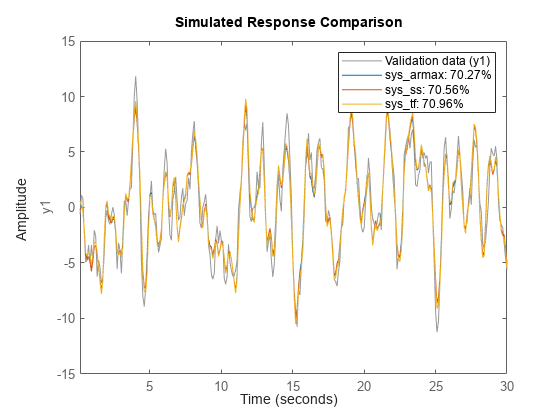
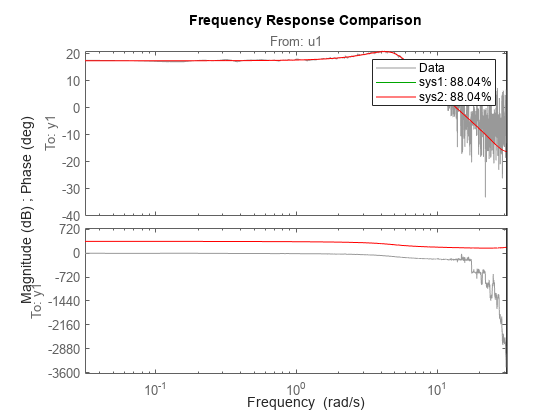
compare( compares the
responses of multiple dynamic systems on the same axes. data,sys1,...,sysN)compare
automatically chooses the line specifications.
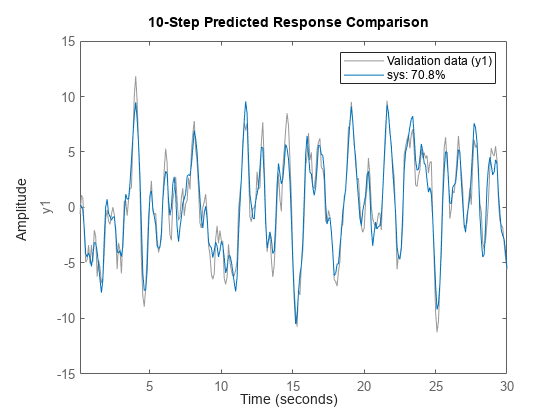
Predict Model Output
compare(___, predicts the
response of kstep)sys, using a prediction horizon specified by
kstep. Prediction uses output measurements as well as input
measurements to project a future response. kstep represents the
number of time samples between the timepoint of each output measurement and the timepoint
of the resulting predicted response.
For more information on prediction, see Simulate and Predict Identified Model Output. You can use this syntax with any of the previous input/output combinations.
Specify Additional Options
Examples
Input Arguments
Output Arguments
Tips
The NRMSE fit result you obtain with
comparemay not precisely match the fit value reported in model identification. These differences typically arise from mismatches in initial conditions, and in the differences in the prediction horizon defaults for identification and for validation. The differences are generally small, and should not impact your model selection and validation workflow. For more information, see Resolve Fit Value Differences Between Model Identification and compare Command.comparematches the input/output channels indataandsysbased on the channel names. Thus, it is possible to evaluate models that do not use all the input channels that are available indata. This flexibility allows you to compare multiple models which were each identified independently from different sets of input/output channels.The
compareplot allows you to vary key parameters. For example, you can interactively control:Whether you generate a simulated or predicted response
Prediction horizon value
Initial condition handling
Which experiment data you view
Which system models you view
To access the controls, right-click the plot to bring up the options menu.
Version History
Introduced in R2006aSee Also
compareOptions | sim | predict | forecast | goodnessOfFit | chgTimeUnit | chgFreqUnit | idplot