impulseest
Nonparametric impulse response estimation
Syntax
Description
sys = impulseest(data)sys, also known as a finite
impulse response (FIR) model, using time-domain or frequency-domain data
data.
data can be in the form of a timetable, a comma-separated pair of numeric matrices, or an iddata object. If
data is a timetable, the software assumes that the last
variable is the single output. You can select specific input and output channels to
use for estimation by specifying the channel names in the
InputName and OutputName name-value
arguments.
The function uses persistence-of-excitation analysis on the input data to select the model order (number of nonzero impulse response coefficients).
Use nonparametric impulse response estimation to analyze input/output data for feedback effects, delays, and significant time constants.
sys = impulseest(___,Name,Value)sys =
impulseest(data,'InputName',["u1","u3"],'OutputName',["y1","y4"]).
You can use this syntax with any of the previous input-argument combinations.
Examples
Input Arguments
Output Arguments
Tips
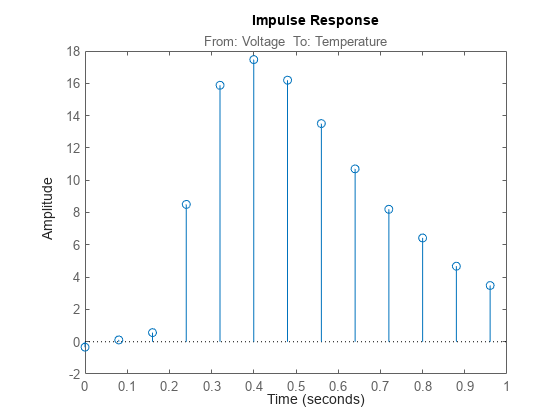
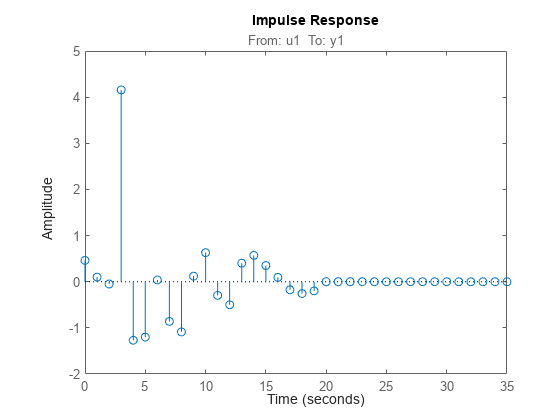
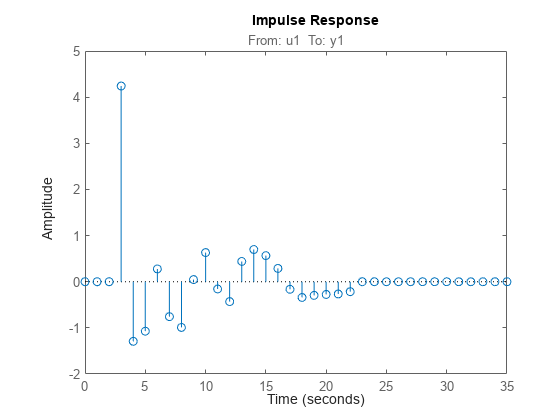
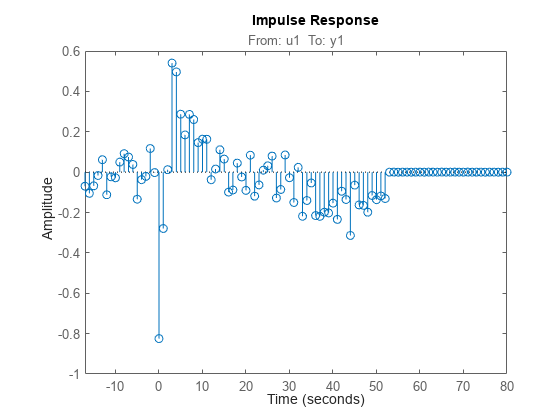
To view the impulse or step response of
sys, use eitherimpulseplotorstepplot, respectively.A response value that corresponds to a negative time value and that is significantly different from zero in the impulse response of
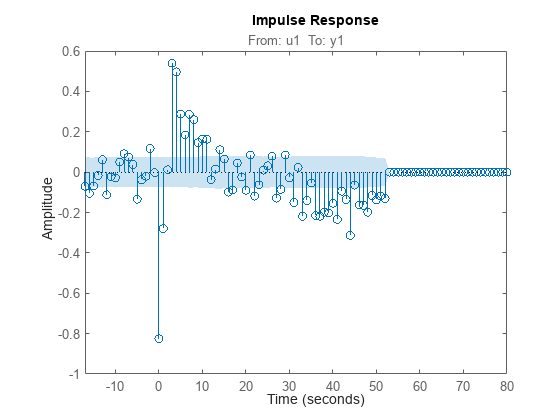
sysindicates the presence of feedback in the data.To view the region of responses that are not significantly different from zero (the zero-response region) in a plot, right-click on the plot and select Characteristics > Confidence Region. A patch depicting the zero-response region appears on the plot. The impulse response at any time value is significant only if it lies outside the zero-response region. The level of confidence in significance depends on the number of standard deviations specified in
showConfidenceor options in the property editor. The default value is 1 standard deviation, which gives 68% confidence. A common choice is 3 standard deviations, which gives 99.7% confidence.
Algorithms
Correlation analysis refers to methods that estimate the impulse response of a linear model, without specific assumptions about model orders.
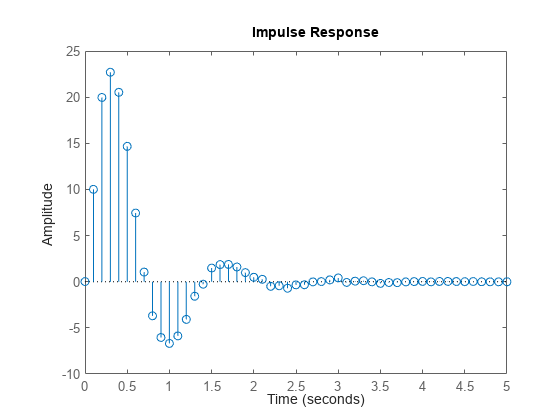
The impulse response, g, is the system output when the input is an impulse signal. The output response to a general input, u(t), is the convolution with the impulse response. In continuous time:
In discrete time:
The values of g(k) are the discrete-time impulse response coefficients.
You can estimate the values from observed input/output data in several different ways.
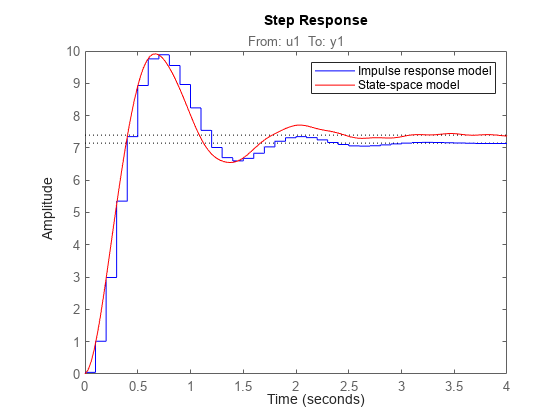
impulseest estimates the first
n coefficients using the
least-squares method to obtain a finite impulse response (FIR) model
of order n.
impulseest provides several important options for the estimation:
Regularization — Regularize the least-squares estimate. With regularization, the algorithm forms an estimate of the prior decay and mutual correlation among g(k), and then merges this prior estimate with the current information about g from the observed data. This approach results in an estimate that has less variance but also some bias. You can choose one of several kernels to encode the prior estimate.
This option is essential because the model order
ncan often be quite large. In cases without regularization,ncan be automatically decreased to secure a reasonable variance.Specify the regularizing kernel using the
RegularizationKernelname-value argument ofimpulseestOptions.Prewhitening — Prewhiten the input by applying an input-whitening filter of order
PWto the data. Use prewhitening when you are performing unregularized estimation. Using a prewhitening filter minimizes the effect of the neglected tail—k>n—of the impulse response. To achieve prewhitening, the algorithm:Defines a filter
Aof orderPWthat whitens the input signalu:1/A = A(u)e, whereAis a polynomial andeis white noise.Filters the inputs and outputs with
A:uf = Au,yf = AyUses the filtered signals
ufandyffor estimation.
Specify prewhitening using the
PWname-value pair argument ofimpulseestOptions.Autoregressive Parameters — Complement the basic underlying FIR model by NA autoregressive parameters, making it an ARX model.
This option both gives better results for small n values and allows unbiased estimates when data are generated in closed loop.
impulseestsets NA to5when t > 0 and sets NA to0(no autoregressive component) when t < 0.Noncausal effects — Include response to negative lags. Use this option if the estimation data includes output feedback:
where h(k) is the impulse response of the regulator and r is a setpoint or disturbance term. The algorithm handles the existence and character of such feedback h, and estimates h in the same way as g by simply trading places between y and u in the estimation call. Using
impulseestwith an indication of negative delays,mi = impulseest(data,nk,nb), wherenk< 0, returns a modelmiwith an impulse responsethat has an alignment that corresponds to the lags . The algorithm achieves this alignment because the input delay (
InputDelay) of modelmiisnk.
For a multi-input multi-output system, the impulse response g(k) is an ny-by-nu matrix, where ny is the number of outputs and nu is the number of inputs. The i–j element of the matrix g(k) describes the behavior of the ith output after an impulse in the jth input.
Version History
Introduced in R2012aSee Also
impulseestOptions | impulse | impulseplot | idtf | step | cra | spa