recursiveLS
Online parameter estimation of least-squares model
Description
Use the recursiveLS
System object™ for parameter estimation with real-time data using a recursive least-squares
algorithm. If all the data you need for estimation is available at once and you are estimating
a time-invariant model, use the offline function mldivide.
To perform parameter estimation with real-time data:
Create the
recursiveLSobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Creation
Syntax
Description
lsobj = recursiveLS
y(t) = H(t)θ(t)+e(t).
Here, y is the output, θ are the parameters,
H are the regressors, and e is the white-noise
disturbance. The default system has one parameter with initial parameter value
1.
lsobj = recursivelS(np)NumberOfParameters property to np.
lsobj = recursivelS(np,theta0)InitialParameters property to theta0.
lsobj = recursiveLS(___,Name=Value)lsobj = recursiveLS(2,EstimationMethod="NormalizedGradient") creates
an estimation object that uses a normalized gradient estimation method.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes. For example, lsobj =
recursiveLS(2,"EstimationMethod","NormalizedGradient") creates an estimation
object that uses a normalized gradient estimation method.
Properties
Unless otherwise indicated, properties are nontunable, which means you cannot change their
values after calling the object. Objects lock when you call them, and the
release function unlocks them.
If a property is tunable, you can change its value at any time.
For more information on changing property values, see System Design in MATLAB Using System Objects.
NumberOfParameters — Number of parameters
1 (default) | positive integer
This property is read-only.
Number of parameters to be estimated, Np, specified as a positive integer.
Parameters — Estimated parameters
[] (default) | positive integer
This property is read-only.
Estimated parameters, stored as a column vector of length
Np, where
Np is equal to
NumberOfParameters.
Parameters is initially empty when you create the object and is
populated after you run the online parameter estimation.
InitialParameters — Initial parameter values
1 (default) | vector of length Np
Initial parameter values, specified as one of the following:
Scalar — All the parameters have the same initial value.
Vector of length Np — The ith parameter has initial value
InitialParameters(i).
When using infinite-history estimation, if the initial parameter values are much
smaller than InitialParameterCovariance, these initial values are
given less importance during estimation. If you have high confidence in the initial
parameter values, specify a smaller initial parameter covariance.
Tunable: Yes
InitialOutputs — Initial values of the output buffer
0 (default) | W-by-1 vector
Initial values of the output buffer in finite-history estimation, specified as
0 or as a W-by-1 vector, where
W is the window length.
Use InitialOutputs to control the initial behavior of the
algorithm.
When InitialOutputs is 0, the object
populates the buffer with zeros.
If the initial buffer is set to 0 or does not contain enough
information, the software generates a warning message during the initial phase of your
estimation. The warning should clear after a few cycles. The number of cycles it takes
for sufficient information to be buffered depends upon the order of your polynomials and
your input delays. If the warning persists, evaluate the content of your signals.
Tunable: Yes
Dependencies
To enable this property, set History to
'Finite'.
InitialRegressors — Initial values of the regressor buffer
0 (default) | W-by-Np array
Initial values of the regressor buffer in finite-history estimation, specified as
0 or as a W-by-Np array,
where W is the window length and Np is the
number of parameters.
The InitialRegressors property provides a means of controlling
the initial behavior of the algorithm.
When the InitialRegressors is set to 0, the
object populates the buffer with zeros.
If the initial buffer is set to 0 or does not contain enough
information, you see a warning message during the initial phase of your estimation. The
warning should clear after a few cycles. The number of cycles it takes for sufficient
information to be buffered depends upon the order of your polynomials and your input
delays. If the warning persists, evaluate the content of your signals.
Tunable: Yes
Dependencies
To enable this property, set History to
'Finite'.
ParameterCovariance — Estimated covariance
[] (default) | Np-by-Np symmetric positive-definite matrix
This property is read-only.
Estimated covariance P of the parameters, stored as an Np-by-Np symmetric positive-definite matrix, where Np is the number of parameters to be estimated. The software computes P assuming that the residuals (difference between estimated and measured outputs) are white noise and the variance of these residuals is 1.
The interpretation of P depends on your settings for the History and EstimationMethod properties.
If you set
Historyto'Infinite'andEstimationMethodto:'ForgettingFactor'— R2 * P is approximately equal to twice the covariance matrix of the estimated parameters, where R2 is the true variance of the residuals.'KalmanFilter'— R2 * P is the covariance matrix of the estimated parameters, and R1 /R2 is the covariance matrix of the parameter changes. Here, R1 is the covariance matrix that you specify inProcessNoiseCovariance.
If
Historyis'Finite'(sliding-window estimation) — R2P is the covariance of the estimated parameters. The sliding-window algorithm does not use this covariance in the parameter-estimation process. However, the algorithm does compute the covariance for output so that you can use it for statistical evaluation.
ParameterCovariance is initially empty when you create the object and is populated after you run the online parameter estimation.
Dependencies
To enable this property, use one of the following configurations:
Set
Historyto'Finite'.Set
Historyto'Infinite'and setEstimationMethodto either'ForgettingFactor'or'KalmanFilter'.
InitialParameterCovariance — Covariance of initial parameter estimates
10000 (default) | positive scalar | vector of positive scalars | symmetric positive-definite matrix
Covariance of the initial parameter estimates, specified as one of these values:
Real positive scalar α — Covariance matrix is an N-by-N diagonal matrix in which α is each diagonal element. N is the number of parameters to be estimated.
Vector of real positive scalars [α1,...,αN] — Covariance matrix is an N-by-N diagonal matrix in which α1 through αN] are the diagonal elements.
N-by-N symmetric positive-definite matrix.
InitialParameterCovariance represents the uncertainty in the
initial parameter estimates. For large values of
InitialParameterCovariance, the software accords less
importance to the initial parameter values and more importance to the measured data
during the beginning of estimation.
Tunable: Yes
Dependency
To enable this property, set History to
'Infinite' and set EstimationMethod to
either 'ForgettingFactor' or
'KalmanFilter'.
EstimationMethod — Recursive estimation algorithm
'ForgettingFactor' (default) | 'KalmanFilter' | 'NormalizedGradient' | 'Gradient'
Recursive estimation algorithm used for online estimation of model parameters, specified as one of the following:
'ForgettingFactor'— Use forgetting factor algorithm for parameter estimation.'KalmanFilter'— Use Kalman filter algorithm for parameter estimation.'NormalizedGradient'— Use normalized gradient algorithm for parameter estimation.'Gradient'— Use unnormalized gradient algorithm for parameter estimation.
Forgetting factor and Kalman filter algorithms are more computationally intensive than gradient and unnormalized gradient methods. However, the former algorithms have better convergence properties. For information about these algorithms, see Recursive Algorithms for Online Parameter Estimation.
Dependencies
To enable this property, set History to
'Infinite'
ForgettingFactor — Forgetting factor for parameter estimation
1 (default) | scalar in the range (0, 1]
Forgetting factor λ for parameter estimation, specified as a scalar in the range (0, 1].
Suppose that the system remains approximately constant over T0 samples. You can choose λ to satisfy this condition:
Setting λ to 1 corresponds to "no forgetting" and estimating constant coefficients.
Setting λ to a value less than 1 implies that past measurements are less significant for parameter estimation and can be "forgotten". Set λ to a value less than 1 to estimate time-varying coefficients.
Typical choices of λ are in the range [0.98, 0.995].
Tunable: Yes
Dependencies
To enable this property, set History to
'Infinite' and set EstimationMethod to
'ForgettingFactor'.
EnableAdapation — Option to enable or disable parameter estimation
true (default) | false
Option to enable or disable parameter estimation, specified as one of the following:
true— Thestepfunction estimates the parameter values for that time step and updates the parameter values.false— Thestepfunction does not update the parameters for that time step and instead outputs the last estimated value. You can use this option when your system enters a mode where the parameter values do not vary with time.Note
If you set
EnableAdapationtofalse, you must still execute thestepcommand. Do not skipstepto keep parameter values constant, because parameter estimation depends on current and past I/O measurements.stepensures past I/O data is stored, even when it does not update the parameters.
Tunable: Yes
DataType — Floating point precision of parameters
'double' (default) | 'single'
This property is read-only.
Floating point precision of parameters, specified as one of the following values:
'double'— Double-precision floating point'single'— Single-precision floating point
Setting DataType to 'single' saves memory but
leads to loss of precision. Specify DataType based on the precision
required by the target processor where you will deploy generated code.
You must set DataType during object creation using a name-value
argument.
ProcessNoiseCovariance — Covariance matrix of parameter variations
0.1 (default) | nonegative scalar | vector of nonegative values | N-by-N symmetric positive semidefinite
matrix
Covariance matrix of parameter variations, specified as one of the following:
Real nonnegative scalar, α — Covariance matrix is an N-by-N diagonal matrix, with α as the diagonal elements.
Vector of real nonnegative scalars, [α1,...,αN] — Covariance matrix is an N-by-N diagonal matrix, with [α1,...,αN] as the diagonal elements.
N-by-N symmetric positive semidefinite matrix.
N is the number of parameters to be estimated.
The Kalman filter algorithm treats the parameters as states of a dynamic system and
estimates these parameters using a Kalman filter.
ProcessNoiseCovariance is the covariance of the process noise
acting on these parameters. Zero values in the noise covariance matrix correspond to
estimating constant coefficients. Values larger than 0 correspond to time-varying
parameters. Use large values for rapidly changing parameters. However, the larger values
result in noisier parameter estimates.
Tunable: Yes
Dependencies
To enable this property, set History to
'Infinite' and set EstimationMethod to
'KalmanFilter'.
AdaptationGain — Adaptation gain
1 (default) | positive scalar
Adaptation gain, γ, used in gradient recursive estimation algorithms, specified as a positive scalar.
Specify a large value for AdaptationGain when your measurements
have a high signal-to-noise ratio.
Tunable: Yes
Dependencies
To enable this property, set History to
'Infinite' and set EstimationMethod to
either 'Gradient' or
'NormalizedGradient'.
NormalizationBias — Bias in adaptation gain scaling
eps (default) | nonegative scalar
Bias in adaptation gain scaling used in the 'NormalizedGradient'
method, specified as a nonnegative scalar.
The normalized gradient algorithm divides the adaptation gain at each step by the
square of the two-norm of the gradient vector. If the gradient is close to zero, this
division can cause jumps in the estimated parameters.
NormalizationBias is the term introduced in the denominator to
prevent such jumps. If you observe jumps in estimated parameters, increase
NormalizationBias.
Tunable: Yes
Dependencies
To enable this property, set History to
'Infinite' and set EstimationMethod to
'NormalizedGradient'.
History — Data history type
'Infinite' (default) | 'Finite'
This property is read-only.
Data history type, which defines the type of recursive algorithm to use, specified as one of the following:
'Infinite'— Use an algorithm that aims to minimize the error between the observed and predicted outputs for all time steps from the beginning of the simulation.'Finite'— Use an algorithm that aims to minimize the error between the observed and predicted outputs for a finite number of past time steps.
Algorithms with infinite history aim to produce parameter estimates that explain all data since the start of the simulation. These algorithms still use a fixed amount of memory that does not grow over time. To select an infinite-history algorithm, use EstimationMethod.
Algorithms with finite history aim to produce parameter estimates that explain only a finite number of past data samples. This method is also called sliding-window estimation. The object provides one finite-history algorithm. To define the window size, specify the WindowLength property.
For more information on recursive estimation methods, see Recursive Algorithms for Online Parameter Estimation.
You must set History during object creation using a name-value argument.
WindowLength — Window size
200 (default) | positive integer
This property is read-only.
Window size for finite-history estimation, specified as a positive integer indicating the number of samples..
Choose a window size that balances estimation performance with computational and memory burden. Sizing factors include the number and time variance of the parameters in your model. WindowLength must be greater than or equal to the number of estimated parameters.
Suitable window length is independent of whether you are using sample-based or frame-based input processing (see InputProcessing). However, when using frame-based processing, your window length must be greater than or equal to the number of samples (time steps) contained in the frame.
You must set WindowLength during object creation using a name-value argument.
Dependencies
To enable this property, set History to 'Finite'.
InputProcessing — Input processing method
'Sample-based' (default) | 'Frame-based'
This property is read-only.
Input processing method, specified as one of the following:
'Sample-based'— Process streamed signals one sample at a time.'Frame-based'— Process streamed signals in frames that contain samples from multiple time steps. Many machine sensor interfaces package multiple samples and transmit these samples together in frames.'Frame-based'processing allows you to input this data directly without having to first unpack it.
The InputProcessing property impacts the dimensions for the
input and output signals when using the recursive estimator object.
'Sample-based'yandestimatedOutputare scalars.His a 1-by-Np vector, where Np is the number of parameters.
'Frame-based'with M samples per frameyandestimatedOutputare M-by-1 vectors.His an M-by-Np matrix.
You must set InputProcessing during object creation using a
name-value argument.
Usage
Description
[
updates and returns the parameters and output of theta,estimatedOutput] = lsobj(y,H)recursiveLS model
lsobj based on real-time output data y and
regressors H.
Input Arguments
y — Output data
real scalar | 1-by-M vector
Output data acquired in real time, specified as one of the following:
When using sample-based input processing, specify a real scalar value.
When using frame-based input processing, specify an M-by-1 vectors, where M is the number of samples per frame.
H — Regressors
1-by-Np vector | M-by-Np
array
Regressors, specified as one of the following:
When using sample-based input processing, specify a 1-by-Np vector, where Np is the number of model parameters.
When using frame-based input processing, specify an M-by-Np array, where M is the number of samples per frame.
Output Arguments
estimatedOutput — Estimated output
real scalar | 1-by-M vector
Estimated output, returned as one of the following:
When using sample-based input processing, returned as a real scalar value.
When using frame-based input processing, returned as an M-by-1 vectors, where M is the number of samples per frame.
The output is estimated using output estimation data, regressors, current
parameter values, and the recursive estimation algorithm specified in the
recursiveLS
System object.
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
Examples
Create System Object for Online Estimation Using Recursive Least Squares Algorithm
obj = recursiveLS
obj =
recursiveLS with properties:
NumberOfParameters: 1
Parameters: []
InitialParameters: 1
ParameterCovariance: []
InitialParameterCovariance: 10000
EstimationMethod: 'ForgettingFactor'
ForgettingFactor: 1
EnableAdaptation: true
History: 'Infinite'
InputProcessing: 'Sample-based'
DataType: 'double'
Estimate Parameters of System Using Recursive Least Squares Algorithm
The system has two parameters and is represented as:
Here,
and are the real-time input and output data, respectively.
and are the regressors,
H, of the system.and are the parameters,
theta, of the system.
Create a System object for online estimation using the recursive least squares algorithm.
obj = recursiveLS(2);
Load the estimation data, which for this example is a static data set.
load iddata3
input = z3.u;
output = z3.y;Create a variable to store u(t-1). This variable is updated at each time step.
oldInput = 0;
Estimate the parameters and output using step and input-output data, maintaining the current regressor pair in H. Invoke the step function implicitly by calling the obj system object with input arguments.
for i = 1:numel(input) H = [input(i) oldInput]; [theta, EstimatedOutput] = obj(output(i),H); estimatedOut(i)= EstimatedOutput; theta_est(i,:) = theta; oldInput = input(i); end
Plot the measured and estimated output data.
numSample = 1:numel(input); plot(numSample,output,'b',numSample,estimatedOut,'r--'); legend('Measured Output','Estimated Output');
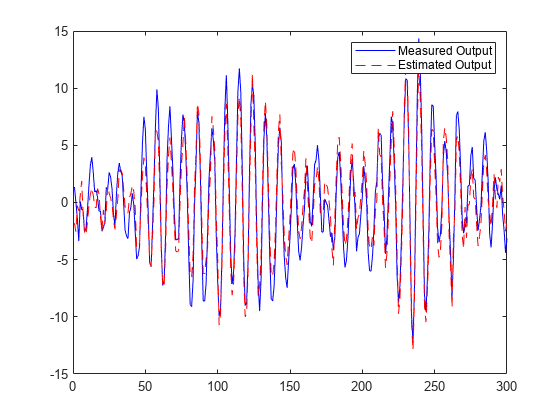
Plot the parameters.
plot(numSample,theta_est(:,1),numSample,theta_est(:,2)) title('Parameter Estimates for Recursive Least Squares Estimation') legend("theta1","theta2")
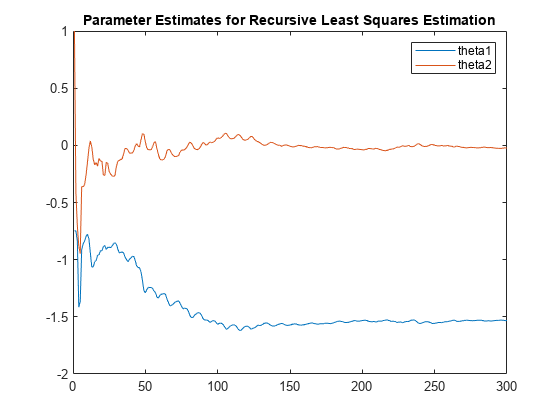
View the final estimates.
theta_final = theta
theta_final = 2×1
-1.5322
-0.0235
Use Frame-Based Data for Recursive Least Squares Estimation
Use frame-based signals with the recursiveLS command. Machine interfaces often provide sensor data in frames containing multiple samples, rather than in individual samples. The recursiveLS object accepts these frames directly when you set InputProcessing to Frame-based.
The object uses the same estimation algorithms for sample-based and frame-based input processing. The estimation results are identical. There are some special considerations, however, for working with frame-based inputs.
This example is the frame-based version of the sample-based recursiveLS example in Estimate Parameters of System Using Recursive Least Squares Algorithm.
The system has two parameters and is represented as:
Here,
and are the real-time input and output data, respectively.
and are the regressors,
H, of the system.and are the parameters,, of the system.
Create a System object for online estimation using the recursive least squares algorithm.
obj_f = recursiveLS(2,'InputProcessing','Frame-Based');
Load the data, which contains input and output time series signals. Each signal consists of 30 frames and each frame contains ten individual time samples.
load iddata3_frames input_sig_frame output_sig_frame input = input_sig_frame.data; output = output_sig_frame.data; numframes = size(input,3)
numframes = 30
mframe = size(input,1)
mframe = 10
Initialize the regressor frame, which for a given frame, is of the form
,
where the most recent point in the frame is .
Hframe = zeros(10,2);
For this first-order example, the regressor frame includes one point from the previous frame. Initialize this point.
oldInput = 0;
Estimate the parameters and output using step and input-output data, maintaining the current regressor frame in Hframe.
The input and output arrays have three dimensions. The third dimension is the frame index, and the first two dimensions represent the contents of individual frames.
Use the
circshiftfunction to populate the second column ofHframewith the pastinputvalue for each regressor pair by shifting the input vector by one position.Populate the
Hframeelement holding the oldest value,Hframe(1,2), with the regressor value stored from the previous frame.Invoke the
stepfunction implicitly by calling theobjsystem object with input arguments. Thestepfunction is compatible with frames, so no loop function within the frame is necessary.Save the most recent input value to use for the next frame calculation.
EstimatedOutput = zeros(10,1,30); theta = zeros(2,30); for i = 1:numframes Hframe = [input(:,:,i) circshift(input(:,:,i),1)]; Hframe(1,2) = oldInput; [theta(:,i), EstimatedOutput(:,:,i)] = obj_f(output(:,:,i),Hframe); oldInput = input(10,:,i); end
Plot the parameters.
theta1 = theta(1,:); theta2 = theta(2,:); iframe = 1:numframes; plot(iframe,theta1,iframe,theta2) title('Frame-Based Recursive Least Squares Estimation') legend('theta1','theta2','location','best')
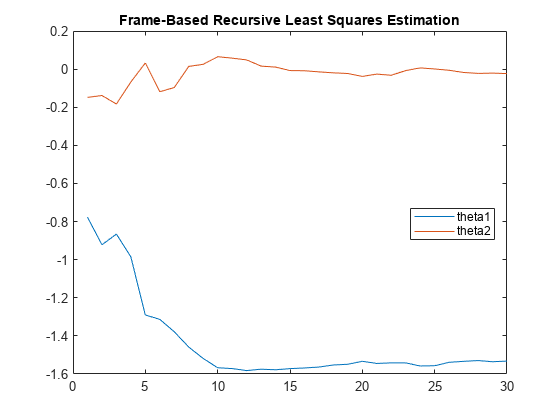
View the final estimates.
theta_final = theta(:,numframes)
theta_final = 2×1
-1.5322
-0.0235
The final estimates are identical to the sample-based estimation.
Specify Initial Parameters for Online Estimation Using Recursive Least Squares Algorithm
Create System object for online parameter estimation using recursive least squares algorithm of a system with two parameters and known initial parameter values.
obj = recursiveLS(2,[0.8 1],'InitialParameterCovariance',0.1);InitialParameterCovariance represents the uncertainty in your guess for the initial parameters. Typically, the default InitialParameterCovariance (10000) is too large relative to the parameter values. This results in initial guesses being given less importance during estimation. If you have confidence in the initial parameter guesses, specify a smaller initial parameter covariance.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
Usage notes and limitations:
For Simulink® based workflows, use Recursive Least Squares Estimator.
For limitations, see Generate Code for Online Parameter Estimation in MATLAB.
Supports MATLAB Function block: No
Version History
Introduced in R2015b
See Also
Functions
Objects
Blocks
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)