Concatenating Models
About Concatenating Models
You can perform horizontal and vertical concatenation of linear model objects to grow the number of inputs or outputs in the model.
When you concatenate identified models, such as idtf,
idpoly, idproc, and
idss model objects, the resulting model combines the
parameters of the individual models. However, the estimated parameter covariance
is lost. If you want to translate the covariance information during
concatenation, use translatecov.
Concatenation is not supported for idgrey models; convert
them to idss models first if you want to perform
concatenation.
You can also concatenate nonparametric models, which contain the estimated
impulse-response (idtf object) and frequency-response
(idfrd object) of a system.
In case of idfrd models, concatenation combines
information in the ResponseData properties of the individual
model objects. ResponseData is an
ny-by-nu-by-nf
array that stores the response of the system, where ny is the
number of output channels, nu is the number of input
channels, and nf is the number of frequency values. The
(j,i,:) vector of the resulting response data represents
the frequency response from the ith input to the
jth output at all frequencies.
Limitation on Supported Models
Concatenation is supported for linear models only.
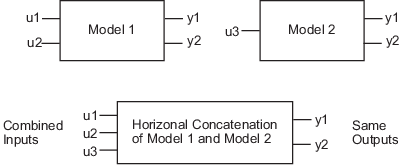
Horizontal Concatenation of Model Objects
Horizontal concatenation of model objects requires that they have the same outputs. If the output channel names are different and their dimensions are the same, the concatenation operation resets the output names to their default values.
The following syntax creates a new model object m that
contains the horizontal concatenation of m1,m2,...,mN:
m = [m1,m2,...,mN]
m takes all of the inputs of m1,m2,...,mN
to the same outputs as in the original models. The following diagram is a
graphical representation of horizontal concatenation of the models.
Vertical Concatenation of Model Objects
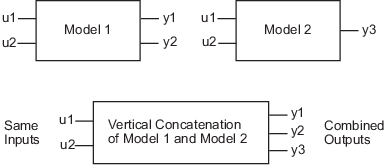
Vertical concatenation combines output channels of specified models. Vertical
concatenation of model objects requires that they have the same inputs. If the
input channel names are different and their dimensions are the same, the
concatenation operation resets the input channel names to their default
('') values.
The following syntax creates a new model object m that
contains the vertical concatenation of m1,m2,...,mN:
m = [m1;m2;... ;mN]
m takes the same inputs in the original models to all of the
output of m1,m2,...,mN. The following diagram is a graphical
representation of vertical concatenation of frequency-response data.
Concatenating Noise Spectrum Data of idfrd Objects
When idfrd models are obtained as a result of estimation
(such as using spa), the SpectrumData
property is not empty and contains the power spectra and cross spectra of the
output noise in the system. For each output channel, this toolbox estimates one
noise channel to explain the difference between the output of the model and the
measured output.
When the SpectrumData property of individual
idfrd objects is not empty, horizontal and vertical
concatenation handle SpectrumData, as follows.
In case of horizontal concatenation, there is no meaningful way to combine the
SpectrumData of individual idfrd
objects, and the resulting SpectrumData property is empty. An
empty property results because each idfrd object has its
own set of noise channels, where the number of noise channels equals the number
of outputs. When the resulting idfrd object contains the
same output channels as each of the individual idfrd
objects, it cannot accommodate the noise data from all the
idfrd objects.
In case of vertical concatenation, this toolbox concatenates individual noise
models diagonally. The following shows that m.SpectrumData is
a block diagonal matrix of the power spectra and cross spectra of the output
noise in the system:
s in m.s is the abbreviation for the
SpectrumData property name.
See Also
If you have the Control System Toolbox™ product, see Combining Model Objects about additional functionality for combining models.
