Estimate State-Space Models in System Identification App
Select Estimate > State Space Models.
The State Space Models dialog box opens.
Tip
For more information on the options in the dialog box, click Help.
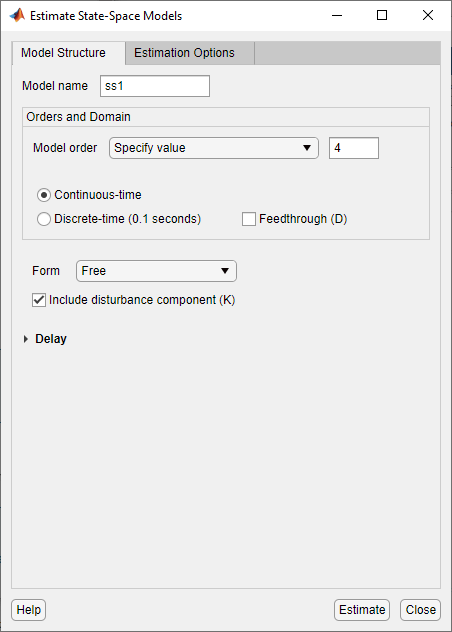
Model name displays the default model name. To change the name, enter a new name. The name of the model must be unique in the Model Board.
Select the Specify value option (if not already selected) and specify the model order in the edit field. Model order refers to the number of states in the state-space model.
Tip
When you do not know the model order, search for and select an order. For more information, see Estimate Model With Selected Order in the App.
Select the Continuous-time or Discrete-time option to specify the type of model to estimate.
You cannot estimate a discrete-time model if the working data is continuous-time frequency-domain data.
Specify the elements to include in the model structure, including feedthrough (D matrix) and the disturbance component (K matrix.) Specify the model form, such as canonical form, by selecting from the options in Form. To specify delays, expand the Delay section.
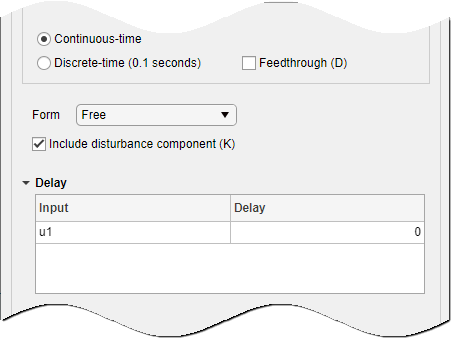
For more information about the type of state-space parameterization, see Supported State-Space Parameterizations.
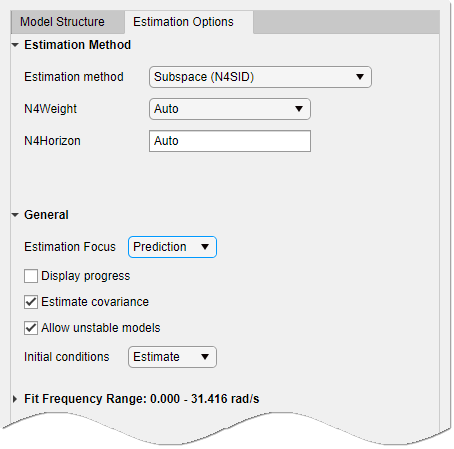
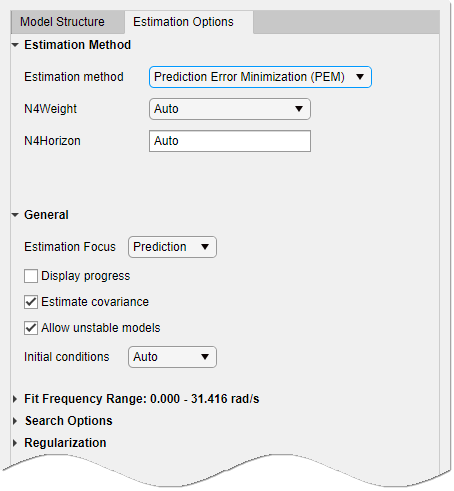
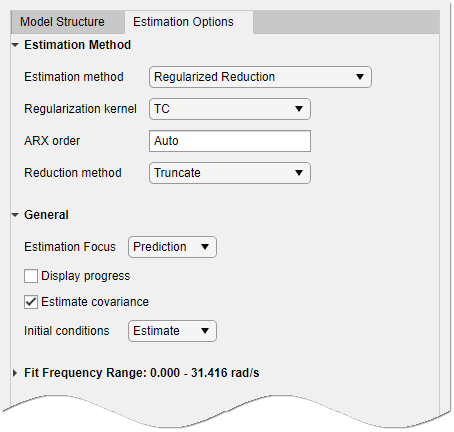
Select the Estimation Options tab to select the estimation method and configure the cost function.
Select one of the methods in Estimation method and configure the options. For more information about these methods, see State-Space Model Estimation Methods.
Click Estimate to estimate the model. A new model gets added to the System Identification app.
Assigning Estimation Weightings
You can specify both how the estimation algorithm weights the fit at various frequencies and what frequency range the app uses. In the app, set Estimation Focus to one of the following options:
Prediction— Uses the ratio of the input spectrum U to the inverse of the noise model H to weight the relative importance of data across the full frequency range. This weighting corresponds to minimizing one-step-ahead prediction, which typically favors the fit over a short time interval. Optimized for output prediction applications.Simulation— Uses the input spectrum only, and not the noise model, for weighting. Optimized for output simulation applications.
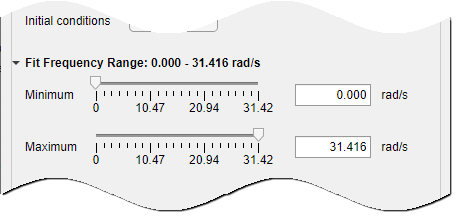
You can apply a passband to limit the frequency range over which the estimation algorithm performs the fit.
For more information on estimation weighting, see the section Effects of
Focus and WeightingFilter Options in Loss Function and Model Quality Metrics.