bwulterode
Ultimate erosion
Description
Examples
Perform Ultimate Erosion of Binary Image
Read a binary image into the workspace and display it.
originalBW = imread('circles.png');
imshow(originalBW)
Perform the ultimate erosion of the image and display it.
ultimateErosion = bwulterode(originalBW); figure, imshow(ultimateErosion)

Input Arguments
BW — Binary image
numeric array | logical array
Binary image, specified as a numeric or logical array of any dimension. For numeric input,
any nonzero pixels are considered to be 1 (true).
Example: BW = imread('circles.png');
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical
method — Distance transform method
'euclidean' (default) | 'quasi-euclidean' | 'cityblock' | 'chessboard'
Distance transform method, specified as one of the values in this table.
Method | Description |
|---|---|
'chessboard' | In 2-D, the chessboard distance between (x1,y1) and (x2,y2) is
max(│x1 – x2│,│y1 – y2│).
|
'cityblock' | In 2-D, the cityblock distance between (x1,y1) and (x2,y2) is
│x1 – x2│ + │y1 – y2│
|
'euclidean' | In 2-D, the Euclidean distance between (x1,y1) and (x2,y2) is
|
'quasi-euclidean' | In 2-D, the quasi-Euclidean distance between (x1,y1) and (x2,y2) is
|
For more information, see Distance Transform of a Binary Image.
conn — Pixel connectivity
4 | 8 | 6 | 18 | 26 | 3-by-3-by- ... -by-3 matrix of 0s and
1s
Pixel connectivity, specified as one of the values in this table. The default
connectivity is 8 for 2-D images, and 26 for 3-D
images.
Value | Meaning | |
|---|---|---|
Two-Dimensional Connectivities | ||
| Pixels are connected if their edges touch. The neighborhood of a pixel are the adjacent pixels in the horizontal or vertical direction. |
Current pixel is shown in gray. |
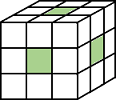
| Pixels are connected if their edges or corners touch. The neighborhood of a pixel are the adjacent pixels in the horizontal, vertical, or diagonal direction. |
Current pixel is shown in gray. |
Three-Dimensional Connectivities | ||
| Pixels are connected if their faces touch. The neighborhood of a pixel are the adjacent pixels in:
|
Current pixel is shown in gray. |
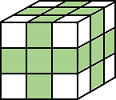
| Pixels are connected if their faces or edges touch. The neighborhood of a pixel are the adjacent pixels in:
|
Current pixel is center of cube. |
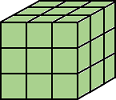
| Pixels are connected if their faces, edges, or corners touch. The neighborhood of a pixel are the adjacent pixels in:
|
Current pixel is center of cube. |
For higher dimensions, bwulterode uses the default value
conndef(ndims(BW),'maximal')
Connectivity can also be
defined in a more general way for any dimension by specifying a 3-by-3-by- ... -by-3 matrix of
0s and 1s. The 1-valued elements
define neighborhood locations relative to the center element of conn. Note
that conn must be symmetric about its center element. See Specifying Custom Connectivities for more information.
Data Types: double | logical
Output Arguments
BW2 — Eroded image
logical array
Eroded image, returned as a logical array of the same size as
BW.
Data Types: logical
Version History
Introduced before R2006a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)