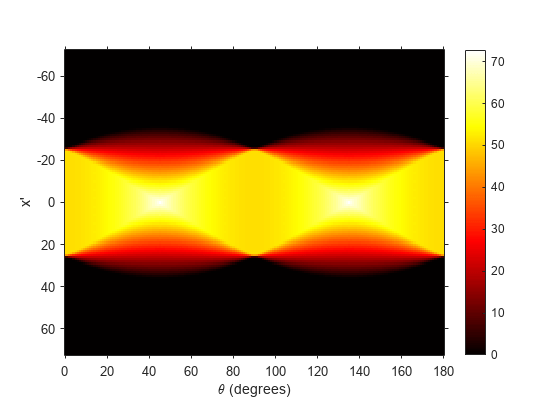
radon
Radon transform
Description
Examples
Input Arguments
Output Arguments
Algorithms
The Radon transform of an image is the sum of the Radon transforms of each individual pixel.
The algorithm first divides pixels in the image into four subpixels and projects each subpixel separately, as shown in the following figure.
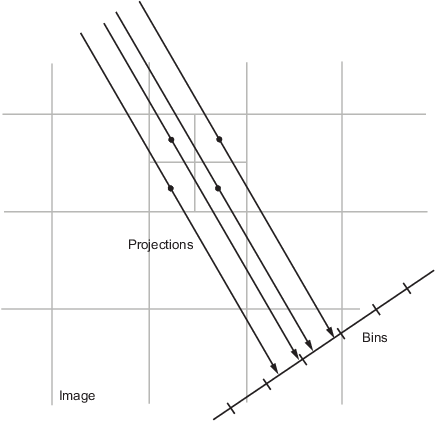
Each subpixel's contribution is proportionally split into the two nearest bins, according to the distance between the projected location and the bin centers. If the subpixel projection hits the center point of a bin, the bin on the axes gets the full value of the subpixel, or one-fourth the value of the pixel. If the subpixel projection hits the border between two bins, the subpixel value is split evenly between the bins.
References
[1] Bracewell, Ronald N., Two-Dimensional Imaging, Englewood Cliffs, NJ, Prentice Hall, 1995, pp. 505-537.
[2] Lim, Jae S., Two-Dimensional Signal and Image Processing, Englewood Cliffs, NJ, Prentice Hall, 1990, pp. 42-45.